58.Асимптоты

При исследовании функций часто бывает, что при удалении координаты х точки кривой в бесконечность кривая неограниченно приближается к некоторой прямой.

Прямая называется асимптотой кривой, если расстояние от переменной точки кривой до этой прямой стремится к нулю при удалении точки в бесконечность.

Но не любая кривая имеет асимптоту. Исследование функций на наличие асимптот имеет большое значение и позволяет более точно определить характер функции и поведение графика кривой. Асимптоты могут быть вертикальные (прямые)(x=a) и наклонные (y=kx+b).

Для нахождения вертикальных асимптот вычисляют предел функции при х→a+0, х→a-0.Если хотя бы один из них равен бесконечности, то x=a – точка разрыва второго рода для функции y=f(x),a прямая х=а – вертикальная асимптота для данной функции.

Для нахождения наклонной асимптоты вычисляются два предела:

k=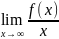 ;b=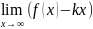 Если оба этих пределов существуют и конечны, то график функции имеет наклонную асимптоту.При этом, в частном случаи, если k=0, то имеем y=b – горизонтальная асимптота.Это исключение наклонной асимптоты.

Если хотя бы один из пределов ; не существуют и не конечны, то наклонная асимптота график функции не имеет.

57.Точки перегиба

Точка, отделяющая выпуклую часть кривой от вогнутой, называется точкой перегиба. В точке перегиба касательная пересекает кривую.

Теорема о необходимом условии точки перегиба.

Если график функции y=f(x) имеет перегиб в точке

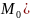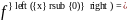, то либо , либо не существует.

Теорема о достаточном условии перегиба.Пусть кривая определяется уравнением y=f(x).Если вторая производная или не

существует и при переходе через точку х= f′′(x) меняет знак, то точка кривой является точкой перегиба.

56. Выпуклость и вогнутость кривой

Кривая обращена выпуклостью вверх на интервале (а, b), если все ее точки лежат ниже любой ее касательной на этом интервале. Кривая, обращенная выпуклостью вверх, называется выпуклой, а кривая, обращенная выпуклостью вниз– называется вогнутой.

Теорема. Если во всех точках интервала(a, b) вторая производная дважды дифференцируемой в этом интервале функции f(x) отрицательна (положительна), то кривая y=f(x) обращена выпуклостью вверх(выпуклостью вниз).

Схема исследования функции на выпуклость, вогнутость

1.Найти вторую производную функции.

2.Найти точки, в которых вторая производная равна нулю или не существует.

3.Исследовать знак производной слева и справа от каждой найденной точки и сделать вывод об интервалах выпуклости и точках перегиба.

55.Исследование функции на экстремум с помощью производных высших порядков.

Если функция f(x) n+1 раз дифференцируема в окрестности точки x0 и все ее производные до производной n - го порядка равны нулю, то есть , то:

если n+1 - нечетное число →в точке перегиб;

если n+1 - четное число→ в точке экстремум.

Если при четном n+1 :

- точка минимума;

точка максимума.

55. Алгоритм для нахождения наибольшего и наименьшего значения(абсолютного максимума и абсолютного минимума)непрерывной

на отрезке [a,b] функции y=f(x):

1)Найти область определения функции.

2) Найти критические точки первого рода.

3)Среди критических точек первого рода оставить только те, которые пренадлежат данному отрезку [a,b].

4)Найти значения функции в найденных критических точках,принадлежащих отрезку [a,b]

5) Найти значения функции на концах отрезка f(a), f(b).

6)Выбрать среди полученных значений наибольшее и наименьшее.

54.Точки экстремума.Достаточное условие существования экстремума.

Пусть функция f(x) определена в некоторой окрестности точки х0 .Функция f(x) имеет в точке х0 максимум(минимум), если для всех точек х≠х0 из этой окрестности выполнено неравенство:

f(x0)>f(x) (f(x0)< f(x)).

Максимум или минимум функции называется экстремумом функции, а те значения аргумента, при которых достигаются экстремумы функции,

Называются точками экстремума функции(точки максимума и точки минимума).

Из определения следует, что экстремум функции имеет локальный характер–это наибольшее или наименьшее значение функции по сравнению с ее близлежащими значениями.

Теорема о достаточном условии существования экстремума. Пусть функция y=f(x) непрерывна в некоторой окрестности критической точки х0, и дифференцируема во всех точках этой окрестности(кроме, может быть, самой точки х0). Тогда если при переходе через точку х0 слева направо производная функции f′(x) меняет знак с“+” на“-“, то в точке х=х0 функция f(x) имеет максимум, а если производная меняет знак с“-“ на“+”, то функция имеет в этой точке минимум. Если при переходе через точку х0 слева направо производная функции f′(x) не меняет знак, то в точке х0 экстремума нет.