17) Линейные операции над векторами.

Для векторов вводятся две линейные операции.

Определение 1. П усть даны два вектора а и b.

П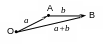 риложим вектор к точке О, получим вектор . Приложим вектор b к точке А, получим вектор . Вектор назовём суммой векторов а и b: .

Определение 2.Пусть задан вектор а и число l. Произведением вектора а на число l называется вектор lа, определяемый следующим образом: длина |lа| = |l|×| |; lа­­а, если l ³ 0 и lа­¯а, если l< 0.

Теорема 1(Свойства линейных операций).

1. (коммутативность сложения):

2. (ассоциативность сложения);

3. а + 0 = 0 + а;

4. l(mа) = (lm)а (ассоциативность умножения на число);

5. (l+m)а = lа + mа;

6. l (а + b) = lа + lb;

7. 0 × а = 0;

8. l × 0 = 0.

Противоположным к вектору а называется вектор (– а), имеющий такую же, как и вектор а длину, но противоположное вектору а направление. Нетрудно видеть, что (– а) = (–1) × а.

Разностью векторов а и b назовём сумму векторов а и (– b): а – b = a + (– b).

Определение 13. Отношением двух коллинеарных векторов а и b, , называется число, определяемое равенством

Всегда lа || а . Если a|| b ), то , где . Поэтому имеет место Теорема 2. a|| b тогда и только тогда, когда при некотором .

18) Линейная зависимость и линейная независимость векторов.

Определение 1. Пусть даны векторы . Вектор вида , где скаляры, называется линейной комбинацией векторов .

Определение 2. Векторы называются линейно независимыми, если

.

В противном случае векторы называются линейно зависимыми.

Теорема 1(Свойства линейно зависимых и линейно независимых систем векторов).

1) Система векторов линейно зависима один из этих векторов есть линейная комбинация остальных.

2) Если среди векторов есть нулевой, то они составляют линейно зависимую систему.

3) Если система векторов содержит линейно зависимую подсистему, то вся система линейно зависима.

4) Если система векторов линейно независима, то и любая ее подсистема линейно независима.

Теорема 2. Два вектора линейно зависимы тогда и только тогда, когда они коллинеарны.

Теорема 3. Три вектора линейно зависимы тогда и только тогда, когда они компланарны.

Теорема 4. Любые четыре вектора линейно зависимы.

19) Базис на плоскости и в пространстве.

Определение 1. Упорядоченная система линейно независимых векторов, лежащих на данной прямой (в данной плоскости, пространстве), называется базисом на этой прямой (на этой плоскости, в пространстве), если любой вектор, лежащий на данной прямой (в данной плоскости, пространстве) представим в виде линейно комбинации векторов этой линейно независимой системы.

Теорема 1. Любой ненулевой вектор, лежащий на данной прямой, образует базис на этой прямой.

Теорема 2. Любая пара неколлинеарных векторов, лежащих в данной плоскости, образует базис на этой плоскости.

Теорема 3. Любая тройка некомпланарных векторов образует базис в пространстве.

Определение 2. Представление вектора в виде линейной комбинации элементов некоторого базиса называется разложением данного вектора по этому базису. Если базис и , то числа называются координатами вектора в данном базисе.

Теорема 4. Разложение вектора по базису единственно.

Теорема 5. При сложении векторов одноименные координаты складываются. При умножении вектора на число все его координаты умножаются на это число.

Теорема 6.

1) Векторы и равны тогда и только тогда, когда равны их координаты.

2) Векторы и коллинеарны тогда и только тогда, когда их координаты пропорциональны.