11) Ступенчатые матрицы.

Определение1. Ступенчатой матрицей будем называть матрицу, удовлетворяющую следующим двум условиям:

1) все нулевые строки находятся ниже всех ненулевых;

2) у каждой ненулевой строки, кроме первой, число нулевых элементов, предшествующих первому ненулевому, больше, чем у предыдущей строки.

Например, ступенчатыми являются матрицы

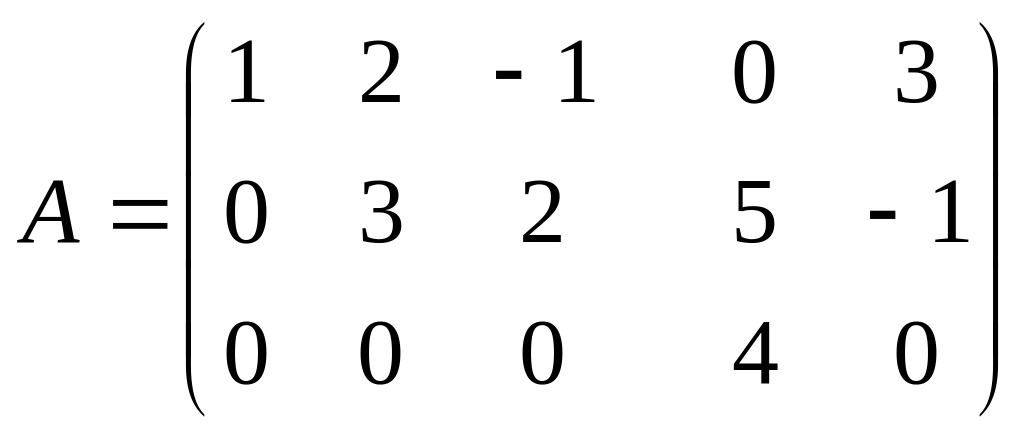
Частным случаем ступенчатой матрицы является треугольная матрица вида

Теорема1. Ранг ступенчатой матрицы равен числу ее ненулевых строк.

12) Элементарные преобразования матриц.

Определение 1. Под элементарными преобразованиями матрицы понимаем:

1) перестановку строк;

2) умножение какой-либо строки на число, отличное от нуля;

3) сложение строк;

4) те же операции со столбцами.

Определение 2. Матрицы, полученные одна из другой элементарными преобразованиями, называются эквивалентными.

Эквивалентность матриц обозначается символом ~: ~ ( эквивалентна )

Теорема 1. Элементарные преобразования матрицы не меняют ее ранга.

Теорема 2. С помощью элементарных преобразований любую матрицу можно привести к ступенчатому виду.

13) Системы линейных алгебраических уравнений.

Определение 1. Системой линейных алгебраических уравнений с неизвестными называется система уравнений вида

(1)

Здесь ( ) называются неизвестными системы; числа коэффициентами при неизвестных, или коэффициентами системы; числа свободными членами. Определение 2. Решением системы (1) называется совокупность чисел которые при подстановке в систему вместо , соответственно, все уравнения системы обращают в тождества.

Определение 3. Система называется совместной, если у нее есть хотя бы одно решение, и несовместной в противном случае.

Определение 4. Совместная система называется определенной, если у нее только одно решение, и неопределенной в противном случае.

Определение5. Две системы называются равносильными, если у них одно и тоже множество решений.

Определение 6. Матрица

A= ,

составленная из коэффициентов системы, называется матрицей системы.

Введем еще две матрицы-столбца: - столбец неизвестных; -столбец свободных членов. Тогда, используя правило умножения матриц, систему

(1) можно записать в матричной форме:

(2)

Определение 7. Система уравнений (1) называется крамеровской, если число

уравнений равно числу неизвестных. Матрица крамеровской системы квадратная, столбцы и - одной размерности. Определитель матрицы системы называется в этом случае определителем системы. Предположим, что Тогда матрица имеет обратную. Следовательно, решение системы запишется в виде