8.2. Общий алгоритм решения задачи компенсации реактивной мощности.

Компенсация реактивной мощности на предприятии является сложной многокритериальной задачей. Наибольший экономический эффект может быть получен при оптимальном распределении конденсаторных установок между напряжениями 0,4 кВ и 10 кВ (6 кВ) сети, а также распределением конденсаторов в узлах сети 10 кВ (6 кВ) и использования возможности выработки реактивной мощности синхронными электродвигателями.

В данном курсовом проекте предлагается следующий алгоритм решения задачи компенсации реактивной мощности по предприятию.

1 Выбор мощности конденсаторных батарей для ТП 10/0,4кВ (6/0,4кВ).

Мощность конденсаторных батарей для i-й ТП 10/0,4 кВ (6/0,4 кВ) определяется по средним нагрузкам исходя из заданного значения

.

Определить суммарную реактивную мощность конденсаторов на стороне 0,4кВ:

2. Определить суммарную реактивную мощность по предприятию с учетом компенсации реактивной мощности на стороне 0,4 кВ.

где - средняя реактивная мощность потребителей на стороне 0,4кВ;

средняя реактивная мощность потребителей на стороне 10 кВ (6кВ);

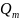- суммарная мощность потерь реактивной мощности в трансформаторах 10/0,4 кВ (6/0,4) кВ (см. раздел 2.5);

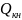- суммарная мощность конденсаторных установок на стороне 0,4 кВ.

3. Определить необходимую мощность конденсаторных установок (с учетом синхронных электродвигателей) на стороне 10 кВ (6кВ).

, .

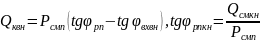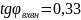Если на предприятии в составе электроприёмников имеются высоковольтные синхронные электродвигатели, то их необходимо использовать для компенсации реактивной мощности. В этом случае мощность конденсаторных установок можно уменьшить на величину реактивной мощности, которую можно получить от синхронных электродвигателей, работающих в режиме перевозбуждения, т.е. с опережающим током (с отрицательной реактивной мощностью).

Мощность синхронных электродвигателей, которую они могут вырабатывать определяется по паспортным данным номинального 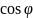в режиме перевозбуждения

Реактивную мощность синхронного электродвигателя (емкостную) приближенно можно определить по формуле:

,

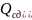
где = ),

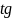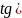- номинальный синхронного электродвигателя при работе его с опережающим током статора; определяется по паспорту электродвигателя.

В данном проекте можно принять , т.е.

С учетом синхронных электродвигателей требуемая мощность конденсаторных установок по заводу уменьшится и будет равна:

.

8.3 Распределение конденсаторов в сети системы электроснабжения.

Потери активной мощности в линии (в трансформаторе), обусловленные передаваемыми активными и реактивными нагрузками, определяется по формуле

кВт,

или

кВт, (1)

где P и Q -активная и реактивная нагрузки, соответственно, кВт и квар; U - напряжение, кв; R-активное сопротивление одной фазы линии (трансформатора), Ом; 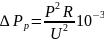- потери активной мощности, вызванные активной нагрузкой, кВт; - то же, но реактивной нагрузкой, кВт.

Потери мощности 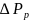практически не зависят от установки конденсаторов и поэтому при сопоставлении потерь в вариантах далее рассматриваются только потери активной мощности , вызванное реактивной нагрузкой Q . Для упрощения обозначений далее вместо будет применяться .

Величину обозначим а, и тогда

кВт (2)

Примем следующие обозначения:

- расчетные реактивные нагрузки линий, квар; - общая расчетная реактивная нагрузка линий, квар; 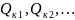- оптимальные мощности конденсаторов, подлежащих установке на отдельных линиях, квар; + - суммарная заранее заданная мощность конденсаторов, подлежащих распределению, квар; - активные сопротивления одной фазы отдельных линий, ом; 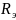эквивалентное сопротивление линий, ом, определяемое из выражения

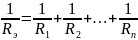(3)

R _n

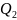
R₁

R _{2 …}

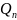
1

2

3

i

n

Q₁

Q₂

Q₃

Q_i

Q_n

R₁

R₂

R₃

R_i

R_n

Рис. 1. Расчетная схема радиальной сети в общем виде.

Вначале рассмотрим схему, состоящую из двух отходящих линий, а затем полученные выводы распространим на большое число линий: три, четыре и т.д. (рис. 1).

Потери активной мощности каждой из двух рассматриваемых линий, обусловленные реактивными нагрузками, составляют по формуле (2):

и , а после установки в конце каждой линии конденсаторов мощностью соответственно и 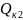суммарные потери в обеих линиях составят:

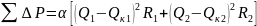. (4)

Найдем условия экстремума предварительно обозначив :

.

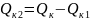Положительный знак второй производной указывает на то, что в указанных условиях имеет минимум; это соответствует наименьшим потерям в сетях.

Нетрудно доказать, что

Указанные выводы (для двух линий) можно распространить на случай с любым количеством отходящих линий. Тогда

, квар ом.

Откуда (5)

Из формулы (5) следует, что при оптимальном распределении конденсаторов в радиальных сетях оставшиеся не скомпенсированные реактивные нагрузки (выражения в скобках) должны быть прямо пропорциональны проводимостям этих линий.

П р и м е р 1: Заданные значения приведены на рис. 2. Кроме того, = 400 квар;U_н = 0,38 кв. Конденсаторы трехфазные единичной номинальной мощностью 10 квар.

Р е ш е н и е: Определим Q=160+300+ =640 квар;

Oм;

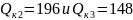квар Oм. Далее откуда Аналогично находим квар.

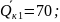
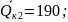
Окончательно с учетом принимаемой единичной мощности конденсаторов 10 квар получаем квар.

1

3

2

R₁=0,05Oм

0,08Oм

0,05

0,04

0,08 Ом

0,04Oм

200 квар

160

300

200 квар

160 квар

300 квар

Рис. 2. Расчетная схема радиальной сети для примера 1.

Для более наглядной демонстрации влияния сопротивлений кабельных линий радиальной сети на распределения мощности конденсаторных батарей рассмотрим следующий пример:

Пример 2. Сопротивления линий остаются такими же как и в предыдущем примере и приведены на рис. 3. Мощность конденсаторов остаются той же Q_n=400 квар; U_n = 0,38 кВ.

R₁=0,05Oм

0,08Oм