Численное решение уравнений с частными производными. Метод сеток . Лекция 28

 Лекция № 28 

1. Метод сеток или метод конечных разностей.

Метод сеток, или метод конечных разностей, является одним из распространённых методов численного решения уравнений с частными производными.

В его основе лежит идея замены фигурирующих в уравнении частных производных конечно-разностными отношениями различной степени точности. При изучении метода сеток мы ограничимся случаем двух независимых переменных.

Пусть в плоскости xО y имеется некоторая область с границей Г (рис. 1).

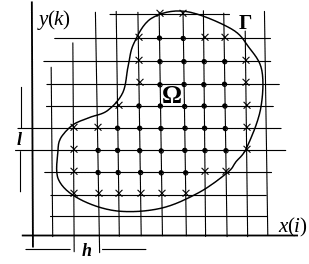
Рисунок 1 – иллюстрация к методу сеток

Построим на плоскости xО y два семейства параллельных прямых:

x= x₀ + ih, ( i = 0,  1,  2, ...),

y = y₀ + kl, (k = 0,  1,  2, ...).

Точки пересечения этих прямых назовём узлами. Два узла называются соседними, если они удалены друг от друга в направлении оси О x или О y на расстояние, равное шагу сетки h или l соответственно.

Выделим только те узлы, которые принадлежат области = + Г. Те из них, у которых все четыре соседних узла принадлежат этому множеству, назовём внутренними узлами (на рис. 1 внутренние узлы обозначены точками). Множество внутренних узлов назовём сеточной областью.

Те узлы, у которых хотя бы один соседний узел не принадлежит к рассматриваемому множеству внутренних узлов, назовём граничными, а совокупность граничных узлов назовём границей сеточной области (на рис. 1 граничные узлы обозначены крестиками).

Возвращаясь к рассмотренным выше постановкам задач математической физики будем считать, что искомая функция u(x, y), т.е. решение дифференциального уравнения с частными производными, ищется в расчётной области = + Г, на границе которой заданы соответствующие граничные условия.

Значения искомой функции u(x, y) в узлах рассмотренной сетки будем далее обозначать через u_ik(x, y) = u_k(x_i, y_k) = u(x₀ + ih, y₀ + kl).

Пользуясь формулами аппроксимации первой производной:

,  _i( x _i1; x _i+1); (1)

, (x_i; x_i+1). (2)

запишем выражения для замены в узлах сетки частных производных первого порядка по пространственным переменным соответствующими разностными отношениями.

В каждом внутреннем узле сетки заменим в соответствии с формулой (1) частные производные первого порядка симметричными разностными отношениями второго порядка точности:

, или

, (3)

В граничных узлах рассматриваемой сетки для замены частных производных первого порядка будем использовать менее точную аппроксимацию производной (2) в виде несимметричного разностного отношения первого порядка точности:

, или

, (4)

Далее, пользуясь формулой аппроксимации второй производной:

, _i(x_i–1; x_i+1) (5)

запишем выражения для замены во внутренних узлах сетки частных производных второго порядка по пространственным переменным соответствующими разностными отношениями.

, или

, (6)

Указанные замены производных в каждом узле сетки позволяют свести решение уравнений с частными производными к решению системы разностных уравнений.

2. Метод сеток решения краевых задач для уравнений эллиптического типа.

Рассмотрим метод сеток решения краевых задач для уравнений эллиптического типа на примере первой краевой задачи (задачи Дирихле) для уравнения Пуассона.

Как известно первая краевая задача, или задача Дирихле для уравнения Пуассона:

u = (7)

ставится следующим образом: найти функцию u = u(x, y), удовлетворяющую внутри некоторой области уравнению (7), а на границе области Г  условию:

=  (x,y) (8)

где  (x,y) заданная непрерывная функция.

Для решения задачи, выбрав шаги h и l по осям x и y соответственно, строим сетку:

x = x₀ + ih, ( i = 0,  1,  2, ...),

y = y₀ + kl, ( k = 0,  1,  2, ...).

применительно к которой уравнение (7) следует переписать в виде:

(9)

При замене в каждом внутреннем узле (x_i, y_k) сетки производных и конечно-разностными отношениями (6), дифференциальное уравнение (9) перепишем в виде системы конечно-разностных уравнений:

, (10)

где f_ik = f (x_i, y_k), i = 0,  1,  2, ... n; k = 0,  1,  2, ... m.

Уравнения (10) вместе со значениями u_ik в граничных узлах, определяемыми из условия (8), образуют систему линейных алгебраических уравнений относительно значений функции u(x, y) в узлах (x_i, y_k) сетки. В такой системе число неизвестных будет равно числу уравнений. И если такая система разрешима, то, решив её, получим приближённые значения искомого решения на конечном множестве точек, являющихся внутренними узлами области .

Наиболее простой вид система разностных уравнений (10) имеет для случая, когда область является прямоугольником с l = h (рис. 2). В этом случае шаг сетки можно подобрать так, чтобы граничные узлы сетки располагались на границе Г рассматриваемой области , на которой в соответствии с (8) как раз и задаются граничные условия.

Для рассматриваемого случая во внутреннем узле i, k сетки уравнения (10) записываются следующим образом:

(10)

В этом случае фигурирующие в уравнениях (10) значения функции u(x, y) в граничных узлах в точности равны значениям граничной функции из граничных условий (8).

Если в уравнении (7) правая часть равна нулю, т.е. f(x, y)  0, мы имеем дело с уравнением Лапласа и соответствующие конечно-разностные уравнения (10) перепишутся в виде:

(11)

При составлении уравнений (10), (11) была использована схема узлов, представленная на рис. 2(а, б). Здесь и в дальнейшем на рисунках будут указываться только индексы узлов сетки, т.е. без указания наименований самих независимых переменных x и y. Например, узел (x_i, y_k) обозначается через (i, k).

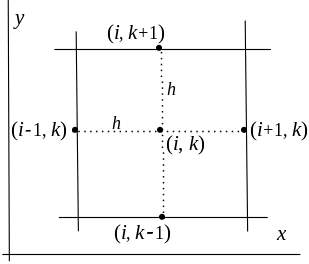
Рисунок 2а – ячейка сетки прямоугольной области

Рисунок 2б – вид прямоугольной области

В рассмотренных разностных схемах (10), (11) для каждого внутреннего узла i, k участвуют 4 соседних узла, расположенные «по кресту» (рис. 2а). Поэтому представленную на рис. 2а схему связи узлов называют центрально симметричным шаблоном сетки или «крестообразным» шаблоном для уравнения Лапласа (Пуассона). В литературе, посвящённой конечно разностным схемам решения уравнений с частными производными, шаблоном конечноразностной схемы называют её геометрическую интерпретацию на конечно-разностной сетке.

Иногда бывает удобнее использовать другую связь узлов в сетке, которая показана на рис. 3(а, б).

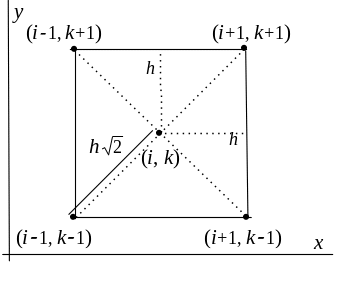
Рисунок 3а – шаблон сетки с альтернативной связью узлов

Рисунок 3б – вид прямоугольной области с альтернативным шаблоном

В этом случае во внутренних узлах сетки (рис. 3) формулы для аппроксимации частных производных второго порядка по пространственным переменным имеют вид:

, (12)

При замене в каждом внутреннем узле (x_i, y_k) сетки производных и конечно-разностными отношениями (12), дифференциальное уравнение Пуассона (9) перепишется в виде системы конечно-разностных уравнений:

, или

отсюда получаем: или

(13)

Аналогично для уравнения Лапласа (f(x, y)  0) на альтернативной сетке будем иметь:

(14)

В рассмотренных разностных схемах (10), (11), (13), (14) число уравнений равно числу внутренних узлов сетки, и поскольку в данном случае граничные узлы сеток лежат на границе Г области , то для каждого слоя (т.е. линии сетки) к ним добавляется ещё по два уравнения, получаемые из граничных условий (8). В результате число уравнений полученной алгебраической системы будет равно числу неизвестных (т.е. числу неизвестных значений функции во внутренних и граничных узлах сеточной области).

3. Оценка погрешности разностного метода решения задачи Дирихле.

Очевидно, что погрешность приближённого решения задачи Дирихле для уравнения Пуассона или Лапласа, полученного разностным методом, складывается из трёх составляющих:

1. погрешность замены дифференциального уравнения разностным уравнением;

2. погрешность аппроксимации краевых условий;

3. погрешность метода решения, полученной системы разностных уравнений.

Оценим погрешность замены дифференциального уравнения разностным уравнением. Очевидно, что данная погрешность определяется погрешностью используемых аппроксимаций производных второго порядка. Так в соответствии с формулой (5) имеем:

, _i(x_i–1; x_i+1)

, _k(x_k–1; x_k+1)

Поэтому в данном случае погрешность замены дифференциального уравнения (7) разностным уравнением (10) равна:

, где (15)

4. Аппроксимация граничных условий для задачи Дирихле.

Решая методом сеток краевую задачу Дирихле для дифференциального уравнения в частных производных, мы заменяем заданную расчётную область с границей Г, на которой заданы граничные условия, сеточной областью с границей из граничных узлов. Как правило, все граничные узлы не будут располагаться на границе Г, а какая-то их часть будет расположена внутри области (рис. 1). То есть, как это показано на рис. 1, только некоторые граничные узлы сетки лежат точно на границе Г области (где в соответствии с постановкой краевой задачи заданы граничные условия), а большая их часть расположена около границы Г внутри области .

Поэтому актуальной является задача замены граничных условий для дифференциального уравнения граничными условиями для разностного уравнения, составляемого только для внутренних узлов сетки, даже в случае задачи Дирихле. При других типах краевых задач условия на границе будут содержать производные искомого решения, которые при переходе к разностным уравнениям должны быть заменены разностными отношениями, например, по формулам (4). Таким образом, почти всегда приходится решать задачу аппроксимации граничных условий.

Итак, рассмотрим проблему аппроксимации граничных условий на примере задачи Дирихле для уравнения эллиптического типа:

u = (7)

=  (x,y) (8)

В этом случае для каждого внутреннего узла i, k сетки дифференциальное уравнение (7) равносильно разностному уравнению:

, (10)

Как уже отмечалось, если расчётная область , на границе Г которой заданы граничные условия (8), является прямоугольником, то подбором значений шагов сетки h и l можно добиться того, чтобы граница сеточной области целиком располагалась на границе Г области . В этом случае никакой интерполяции граничных условий (8) не потребуется, поскольку значения искомого решения на границе сетки в точности равны значениям заданным на границе Г граничными условиями (8), приводимыми при постановке данной задачи математической физики.

В том случае, когда расчётная область не является прямоугольником, как это, например, представлено на рис. 1, то часть узлов границы сеточной области не попадёт на границу Г и будет лежать где-то внутри (на расстоянии, меньшем, чем шаг h или l, от границы Г). Следовательно, значения функции на границе сетки (не лежащие на Г) будут неизвестны, и их необходимо доопределить каким-то образом.

В этом случае значения искомого решения в граничных узлах полагают равными значениям заданной функции  (x) в точках Г, ближайших к этим узлам. Иногда этот «снос» значений выполняют из точки Г, ближайшей к данному граничному узлу, в направлении одной из осей координат (рис. 4).

Выполняя указанное доопределение значений искомого решения в граничных узлах сетки мы вносим погрешность, величина которой зависит от близости границы Г и прилегающих к ней граничных узлов сетки. Очевидно, что снесённое в граничный узел значение решения будет отличаться от значения истинного решения краевой задачи в этом узле на величину порядка расстояния этого узла от точки Г, из которой происходит снос.

Рисунок 4 – аппроксимация граничных условий

Только в том случае, когда все граничные узлы попадут на Г, перенос граничных условий делать не нужно, и мы не вносим никакой дополнительной погрешности в искомое решение краевой задачи. Поэтому сетку целесообразно выбирать так, чтобы граница сеточной области и граница Г области располагались бы максимально близко друг к другу. Для этого иногда целесообразно отказаться от квадратной сетки, а рассматривать прямоугольную сетку или треугольную сетку, или вообще какую-либо другую.

Простой способ уменьшения погрешности, связанной со сносом в граничный узел краевого значения решения, состоит в том, чтобы неизвестное значение функции u_А в граничном узле А выразить в виде линейной комбинации значения функции u_С в ближайшем внутреннем узле С и краевого значения решения  _B в ближайшей точке В границы Г расчетной области (рис. 4):

u_А.= (16)

Говоря иначе, данный подход к уменьшению погрешности заключается в интерполяции значения u_А в граничном узле А на основе значения решения во внутреннем узле u_С и значения решения  _B в ближайшей точке В границы Г. При этом формула (16) соответствует случаю, когда значение u_А получается линейной интерполяцией значений u_С и  _B.

Действительно, в случае линейной интерполяции предполагается, что значения искомой функции u в промежутке между узлами интерполяции А и С меняется по линейному закону, поэтому можем написать, что:

Выражая отсюда значение u_А, получим уравнение (16), выражающее значения функции u_С в граничном узле А.