Определение фигуры геоида.

Итак, если приравнять гравитационный потенциал, заданный формулой (26), какоё-нибудь константе, получим уравнение поверхности. Эта поверхность будет поверхностью уровня, так как вектор силы тяжести строго перпендикулярен касательной плоскости в любой точке этой поверхности. Если бы вся поверхность была бы залита водой, то она находилась бы в покое, то есть никаких течений бы не наблюдалось. Но какой константе нужно приравнять гравитационный потенциал? Изменяя эту константу, будем иметь семейство эллипсоидов. Если в качестве тела отсчёта выбрать эллипсоид вращения, близкий к поверхности океана, то в качестве фигуры идеальной (нормальной) Земли уместно взять именно этот эллипсоид, который называют общим земным эллипсоидом (ОЗЭ). Определить фигуру Земли (геоида) – это значит определить расстояния всех точек поверхности геоида относительно ОЗЭ, другими словами, чтобы знать фигуру Земли нужно знать высоты геоида относительно эллипсоида.

В середине XIX столетия Стокс показал, что если заданы уровенная поверхность, целиком охватывающая все притягивающие массы, известна также угловая скорость вращения этой массы (планеты), то гравитационный потенциал однозначно определяется во всем внешнем пространстве. Он также сформулировал и обратную задачу. Если гравитационный потенциал и масса известны (известна также и угловая скорость вращения), то можно определить и поверхность уровня, то есть определить фигуру геоида. Тем самым Стокс заложил основы нового направления геодезии – определение фигуры геоида по гравиметрическим данным. Он получил следующую формулу для определения высот геоида относительно эллипсоида

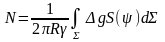, (41)

где 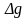– так называемая смешанная гравитационная аномалия, равная разности «наблюдённого» значения силы тяжести g на поверхности геоида и «теоретического» (нормального) значения силы тяжести 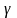на эллипсоиде. Функция 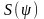имеет достаточно сложный вид:

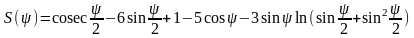
Эта же функция, выраженная через разложение по полиномам Лежандра, выглядит гораздо компактнее

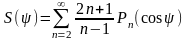(42)

Величина , которая входит в формулы Стокса (41) и (42) есть угол между двумя радиус-векторами. Один из них определяет точку наблюдения, для которой вычисляется высота геоида, а другой – соединяет начало координат с элементом сферы на поверхности, по которой ведётся интегрирование. При выводе формулы (41) предполагалось, что сила тяжести линейно зависит от высоты, а интегрирование ведётся не по эллипсоиду, а по сфере. Поэтому формула Стокса (41) получена в линейном и сферическом приближении.

Отклонение отвесной линии

Отклонение отвесной линии содержит в себе информацию о напряжённости в земной коре и может быть полезной при решении не только геодезических, но и геофизических задач. Остановимся на этом подробнее.

Поскольку отвесная линия или отвес есть нормаль к уровенной поверхности, то есть к поверхности геоида, форма которой зависит от распределения масс внутри земли, от этого распределения зависит и направление отвесной линии. С другой стороны, форма уровенной поверхности зависит от распределения силы тяжести: если две поверхности уровня сближаются, то сила тяжести возрастает, если отдаляются – убывает. Таким образом, измерение силы тяжести и определение отклонений отвесной линии – две задачи тесно связанные друг с другом.

Отвесная линия имеет две компоненты: она, строго говоря, не совпадает с нормалью к общему земному эллипсоиду. Отклонение её на север в плоскости меридиана будем считать положительным, а положительное отклонение в плоскости первого вертикала – отклонение на восток. Будем обозначать эти две составляющие отклонения отвесной линии греческими буквами . Итак, угол 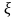– угол, на который отклоняется вертикальная линия в плоскости меридиана , а угол 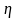определяет отклонение отвесной линии в первом вертикале. Если углы измерять в радианах, то

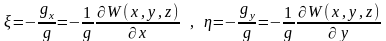(43)

Голландский учёный Ф.А. Венинг-Мейнес показал, что если известны аномалии силы тяжести по всей Земле, обе компоненты отклонения отвесной линии можно вычислить по формуле

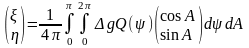, (44) где 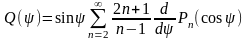. Величина в приведенной формуле, та же, что и в формуле Стокса.

Понятно, что компоненты отклонения отвесной линии можно вычислить по формуле (42), если известны аномалии силы тяжести по всей Земле, что недоступно. Однако их можно вычислить иначе. В случае, когда в данной точке известны и геодезические и астрономические координаты, информацию об отклонении отвесной линии легко получить, сравнивая геодезические и астрономические координаты. Как известно, астрономическая широта равна углу, который образует вертикаль в точке пересечения с плоскостью экватора (небесного), а долгота – это двугранный угол между плоскостями меридиана данной точки и плоскостью «нулевого меридиана» в Гринвиче. Элементарные выкладки приводят к следующим формулам для компонент отклонения отвесной линии

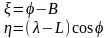(43)

Пункты на земной поверхности, где известны и астрономические и геодезические координаты называют пунктами Лапласа. На эти пункты нужно смотреть как на опорные пункты. Они не могут покрывать поверхность Земли густой сетью. А гравиметрические исследования, выполняются, как правило, в виде площадной съёмки. Современные методы геодезии предусматривают, как астрономо-геодезические, так и гравиметрические измерения. Советский учёный М.С. Молоденский предложил методику так называемого астрономо-гравиметрическое нивелирование, в котором предусмотрены оба эти вида работ.