
- •Гравитационный потенциал материальной точки
- •Гравитационный потенциал системы материальных точек
- •Гравитационный потенциал тела
- •X,y,z через r. Тогда гравитационный потенциал притяжения в точке р будет равен тройному интегралу по всем массам тела:
- •Свойства гравитационного потенциала притяжения
- •Гравитационный потенциал тяжести
- •Аналитическое представление локального гравитационного поля.
- •Аналитическое представление глобального гравитационного поля.
- •Фигуры равновесия небесных тел
- •Геодезические приложения гравиметрии
- •Определение фигуры геоида.
- •Отклонение отвесной линии
- •Современные методы определения фигуры Земли
- •Применение гравиметрических методов в геофизике
- •Методы гравиразведки
- •Свободное падение
- •Маятниковый метод определения силы тяжести
Гравитационный потенциал тяжести
Любое измерение какой-либо физической величины – это сравнение её (если это возможно!) с эталоном. Мы можем измерить массу, сравнивая силу взаимодействия этой массы с другой массой, принятой в качестве эталона (гирьки). Измерение силы тяжести также сопряжено с измерением силы взаимодействия пробного тела и опоры. Тяжесть тела мы ощущаем, когда его поднимаем или просто удерживаем. В приборах, которые называются пружинными гравиметрами, силу тяжести сравнивают с «эталонной» упругой силой пружины. Однако в движении ощущение тяжести связано с ускорением опоры. Каждый пассажир на морском судне знает, что качка корабля влияет на ощущении собственного веса. Если вы неподвижны, но находитесь на поверхности Земли, которая совершает суточное вращение вокруг своей оси, в действительности вы также двигаетесь с ускорением! Но ускорение создаётся силой. Отсутствие силы, согласно законам механики, приводит к равномерному и поступательному перемещению. Откуда же берётся эта сила?
Все предметы, неподвижные относительно поверхности вращающейся Земли совершают вместе с ней вращательное перемещение в инерциальном пространстве, двигаясь с ускорением, которое мы называем центростремительным. Опора, на которой покоится пробное тело, удерживает это тело с помощью силы трения. Но поскольку это тело неподвижно относительно опоры, то оно «сопротивляется» навязанному ему ускорению, подчиняясь закону инерции, оно «хочет» двигаться равномерно и поступательно. Эту силу мы называем центробежной, так как она равна и противоположна по знаку центростремительной силе. Центробежная сила не имеет физической природы подобно гравитационной или электромагнитной, но введение её в рассмотрение существенно облегчает решение задач теоретической механики.
Тем не менее, наибольший вклад в тяжесть пробного тела даёт сила гравитационного притяжения. Вектор силы тяжести создаёт сумма двух сил –
гравитационной
и центробежной. Так же, как для силы
притяжения, вектора удельных сил тяжести
также образуют гравитационного поле.
Силовую функцию для поля сил тяжести
мы будем называть
гравитационным потенциалом тяжести.
В предыдущем разделе мы получили
формулы для гравитационного
потенциала притяжения.
Чтобы получить выражение для гравитационного
потенциала тяжести нужно только добавить
«центробежный потенциал», то есть
силовую функцию для центробежной силы:
 .
.
Здесь W(x,y,z)–
потенциал тяжести, V(x,y,z)
– потенциал притяжения,
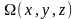 – центробежный потенциал.
– центробежный потенциал.
Для того, чтобы последний выразить через
координаты в явном виде, необходимо
выбрать систему координат. Будем считать,
что ось Oz
совпадает с осью вращения Земли, тогда
оси Ox
и
Oy
будут лежать
в плоскости экватора. Вектор центробежной
силы
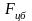 будет иметь две составляющих, лежащие
в плоскости, параллельной плоскости
экватора, поэтому
будет иметь две составляющих, лежащие
в плоскости, параллельной плоскости
экватора, поэтому
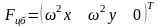 .
Чтобы получить силовую функцию, нужно
проинтегрировать вектор центробежной
силы. После интегрирования получим:
.
Чтобы получить силовую функцию, нужно
проинтегрировать вектор центробежной
силы. После интегрирования получим:
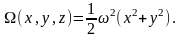 Теперь гравитационный потенциал тяжести
(не притяжения!) принимает вид
Теперь гравитационный потенциал тяжести
(не притяжения!) принимает вид
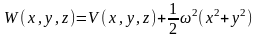 .
(10)
.
(10)
Перейдём теперь к сферической системе координат. Пусть
 ,
(11)
,
(11)
где
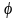 – геоцентрическая широта точки Р,
а
– геоцентрическая широта точки Р,
а
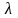 –
долгота этой же точки.
–
долгота этой же точки.
Теперь, с учётом формулы (9) для гравитационного потенциала притяжения, потенциал тяжести принимает вид
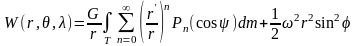 (12)
(12)
Напоминаем,
что точка, в которой определён этот
гравитационный потенциал, имеет
координаты
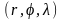 ,
а угол
,
есть угол, который образуют вектора
,
а угол
,
есть угол, который образуют вектора
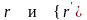 .
.
