Лекции по гравиметрии для астрономов.

Что такое гравиметрия?

Термин гравиметрия происходит от латинского слова gravis – тяжёлый и греческого слова – измеряю. Таким образом, слово «гравиметрия» обозначает «измеряю тяжесть». Что это? Взвешивание? Но тогда мы получим массу! Эта процедура не может быть предметом изучения в нашем курсе! Но тяжесть тел зависит не только от их массы, но и от силы, которая давит на опору, которая удерживает это тело. А эта сила возникает вследствие действия закона Всемирного Тяготения, сформулированного И.Ньютоном и законом движения опоры. В каждой точке пространства, где присутствуют массы, есть и сила тяготения. Её нельзя экранировать или изменять по величине и направлению. Таким образом, гравитационные силы, образуют поле, которое и называют гравитационным. Изучение гравитационного поля Земли или какой-либо другой планеты и составляет предмет нашего курса. Напряжённость этого поля, измеряется силой, отнесённой к единице массы. Она имеет размерность ускорения и поэтому часто эту силу называют ускорением силы тяжести. Этот термин крайне неудачный! Что значит ускорение силы? Сила ускоряется? На наш взгляд лучше сказать , что сила тяжести , отнесённая к единице массы, есть удельная сила тяжести. Впрочем, этот термин не прижился. Мы говорим просто сила тяжести без уточнения, к какому телу она относится.

Наука гравиметрия имеет очень много приложений в различных отраслях знаний, в частности в астрономии, геодезии, геофизике, геологии и даже в навигации. Астрономию нужно считать «родительницей» геодезии и даже той отрасли гравиметрии, которая называется гравиразведкой. Закон Всемирного Тяготения позволил объяснить закономерности в движении планет и дал начало такой науке, как небесная механика, он же позволил объяснить, почему наша планета отличается от сферической. Много точнее её считать имеющей форму эллипсоида вращения. Параметры этого эллипсоида очень важно знать при построении точных карт земной поверхности. Другими словами, гравиметрии находит весьма существенные приложения в геодезии. Геодезия изучает также форму уровенной поверхности нашей планеты, практически совпадающей с уровнем моря, определяет высоты физической поверхности Земли, отклонения отвесной линии от нормали к Общему Земному Эллипсоиду и другие задачи, связанные с распределением силы тяжести по поверхности Земли.

Но сам термин гравиметрия указывает, что наш предмет занимается методами измерения тяжести, что является, скорее задачей прикладной механики. По сути дела, гравиметрия разделилась на две самостоятельные части – науку о закономерностях распределения гравитационного поля в пространстве, лежащую в основе геодезии и геофизики, и науку о методах измерения напряжённости этого поля. Профессор астрономического отделения МГУ, а затем академик, директор Пулковской астрономической обсерватории АН СССР А.А. Михайлов, в своём учебнике « Курс гравиметрии и теории фигуры Земли» пишет «… название нашего предмета можно было бы заменить одним словом – гравилогия, т.е. изучение тяжести или рассуждения о тяжести, но такое название не употребляется ». Хотя существуют же разделы науки геофизики как сейсмология и сейсмометрия! Если первый изучает распространение сейсмических волн в теле Земли, то второй раздел занимается созданием приборов для измерения этих волн. В нашем курсе мы постараемся познакомить, по возможности, с различными аспектами нашего предмета.

Часть первая. Гравитационный потенциал

Гравитационный потенциал материальной точки

Согласно закону Всемирного тяготения, две материальные точки с массами М и т притягиваются друг к другу с силой, прямо пропорциональной их массам и обратно пропорциональной квадрату расстояния между ними. Следовательно, абсолютная величина этой силы равна 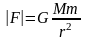, где r – расстояние между ними. Пусть одна из этих материальных точек – «пробное тело» с массой т, тогда напряженность гравитационного поля в этой точке будет равна 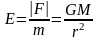. Численно эта

величина равна силе притяжения материальной точки с массой, равной единице. Тогда, если начало координат совместить с притягивающей точкой, имеющей массу М, а радиус-вектор притягиваемой точки , есть r , удельную силу притяжения в точке т можно записать так:

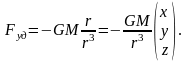(1)

В небесной механике часто пользуются понятием силовой функции, как функции координат х,у,z такой, что производная по любому направлению эвклидова пространства равна составляющей силы по этому направлению. Существует силовая функция и для поля гравитационных сил. Для поля сил гравитирующей (притягивающей) материальной точки с массой М она имеет вид 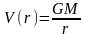(2)

Убедимся в этом. Примем за начало отсчёта притягивающую материальную точку с массой М, тогда расстояние точки Р(x,y,z) от начала координат будет равно 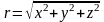. Продифференцируем функцию 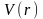по направлениям координатных осей, получим

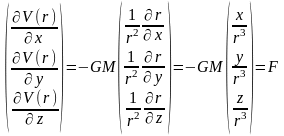(3)

Полученное выражение полностью совпадает с формулой для вектора удельной силы притяжения (1).

В физике используют понятие потенциала, как скалярную величину, равную работе, которую нужно совершить, чтобы отправить пробное тело из

заданной точки в бесконечность. Чтобы отправить точечную единичную массу в бесконечность необходимо проинтегрировать скалярное произведение силы притяжения на вектор перемещения от точки Р, где

находится эта точечная масса, до бесконечности:

.

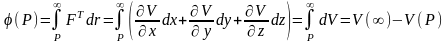Поскольку гравитационный потенциал на бесконечном удалении от притягивающего тела можно считать равным нулю, из полученной формулы следует, что гравитационный потенциал притяжения и силовая функция отличаются только знаком. В дальнейшем под гравитационным потенциалом мы будем понимать именно силовую функцию. Из изложенного следует, что гравитационный потенциал притяжения материальной точки с массой М равен

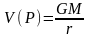. (4)

В качестве учебного пособия для нашего курса мы рекомендуем книгу профессора Н.П. Грушинского «Основы гравиметрии» (Москва, «Наука» Главная редакция физико-математической литературы, 1983.

Гравитационный потенциал системы материальных точек

Предположим, что мы имеем систему материальных точек с массами

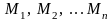, расположенных соответственно на расстояниях 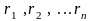от точечного пробного тела с единичной массой, тогда гравитационный потенциал в этой точке будет равен сумме гравитационных потенциалов каждой из притягивающих масс. 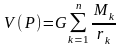Снова в точку Р поместим точечную массу, равную единице , тогда полагая, что гравитационный потенциал обладает свойством суперпозиции , гравитационный потенциал суммы материальных точек равен сумме гравитационных потенциалов каждой из притягивающих масс, то есть (5)