3.2.3 Контрольні питання
1 У чому полягає основна ідея симплекс-методу?
2 У чому полягає економічна інтерпретація симплекс-методу?
3 За яким правилом заповнюється перша симплекс-таблиця?
4 Як визначаються напрямні стовпець і рядок у симплекс-таблиці?
5 Сформулювати правило прямокутника для перерахування симплекс-таблиць.
6 Який план вважається оптимальним?
Практичне заняття №4
Тема: |
Метод штучного базису |
Мета: |
|
Час: |
2 год. |
4.1 Теоретичні відомості
Метод
штучного базису використовується для
визначення максимального значення
цільової функції
(4.1)
при заданій системі обмежень
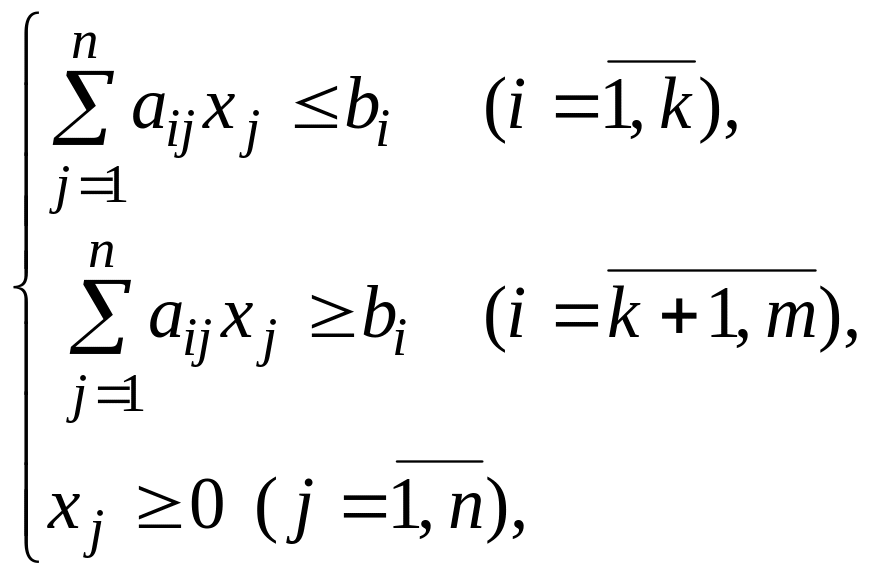(4.2)
де
при умовах, що кількість базисних змінних
менше кількості обмежень.
Розв’язання задачі лінійного програмування методом штучного базису включає наступні етапи:
Приведення ЗЛП (1) – (2) до канонічного виду.
Знайти максимум функції
(4.3)
при умовах
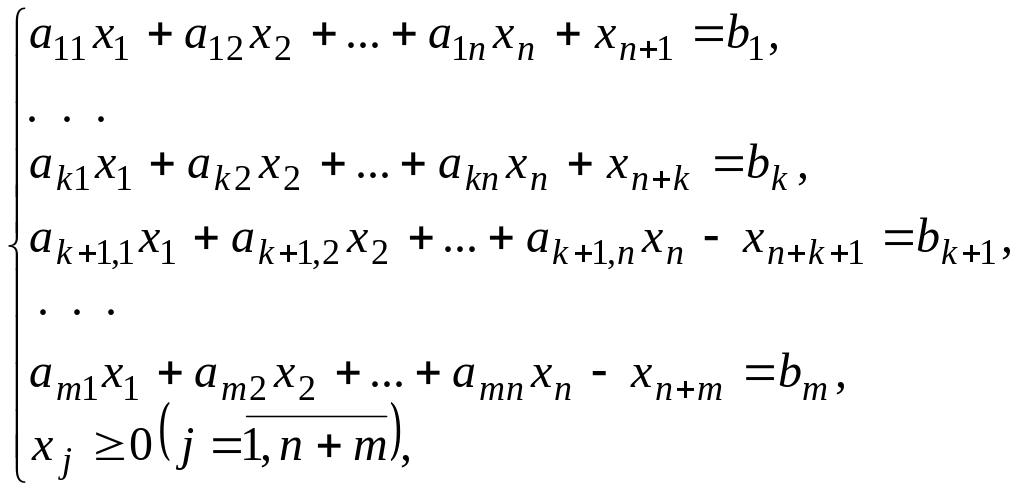(4.4)
де
Змінні
є базисними.
Складання розширеної задачі.
Обмеження
не містять базисні змінні, тому до них
додають змінні
,
та перетворюють цільову функцію. Таким
чином, розширена задача має вигляд:
знайти максимум функції
(4.5)
при умовах
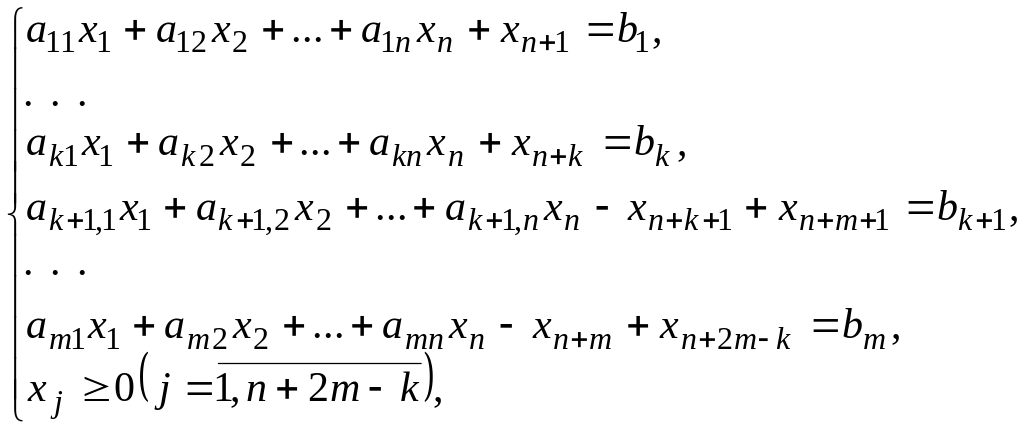(4.6)
де
-
деяке досить велике позитивне число.
Змінні
називаються штучними.
Базисними
є змінні
.
Заповнення першої симплекс-таблиці (таблиця 4.1) для розширеної задачі (5) – (6).
Перша симплекс-таблиця заповнюється за алгоритмом звичайного симплекс-методу.
Визначаються
і
.
У
рядок
поміщають складові, що не містять
,
а в рядок
поміщають коефіцієнти при M.
Опорний план задачі має вигляд
.
4) Перерахування симплекс-таблиць за наступним алгоритмом.
а) Перевіряють наявність штучних змінних у базисі. Якщо не всі штучні змінні виключені з базису, то переходять до п.2. Якщо всі штучні змінні виключені з базису, то переходять до п.4.
б)
Визначають наявність негативних
.
Якщо існують
,
то переходять до п.3. Якщо всі
,
то переходять до п.7.
в) Перераховують таблицю за звичайним алгоритмом симплекс-методу і переходять до нового опорного плану. Переходять до п.1.
г)
Визначають наявність негативних
.
Якщо існує
,
то переходять до п.5. Якщо всі
,
то переходять до п.6.
д)
Якщо існує хоча б одне
то виконують перерахування таблиці і
переходять до п.4. Якщо всі
то переходять до п.7.
є) Оптимальний план задачі (4.1) - (4.2) знайдено.
ж) Задача (1) - (2) не має розв'язків.
Таблиця 4.1 – Перша симплекс-таблиця
|
|
базис
|
|
|
… |
|
|
… |
|
|
… |
|
|
… |
|
|
|
... |
|
|
... |
|
|
... |
|
|
... |
|
|||||
|
|
|
|
|
… |
|
|
… |
|
|
… |
|
|
… |
|
|
. . . |
. . . |
. . . |
. . . |
. . . |
. . . |
. . . |
. . . |
. . . |
. . . |
. . . |
. . . |
. . . |
. . . |
. . . |
. . . |
. . . |
|
|
|
|
|
… |
|
|
… |
|
|
… |
|
|
… |
|
|
|
|
|
|
|
… |
|
|
… |
|
|
… |
|
|
… |
|
|
. . . |
. . . |
. . . |
. . . |
. . . |
. . . |
. . . |
. . . |
. . . |
. . . |
. . . |
. . . |
. . . |
. . . |
. . . |
. . . |
. . . |
|
|
|
|
|
… |
|
|
... |
|
|
… |
|
|
… |
|
|
|
|
|
… |
|
|
… |
|
|
… |
|
|
… |
|
|
||
|
|
|
… |
|
|
… |
|
|
… |
|
|
… |
|
|
||
