1.2.3 Контрольні питання

1 Що називається математичною моделлю задачі лінійного програмування?

2 Постановка загальної, основної і канонічної задачі ЛП.

3 Дати визначення цільової функції ЗЛП.

4 Що називається обмеженнями ЗЛП?

2 Практичне заняття № 2

Тема:	Графічний розв’язок ЗЛП
Мета:	Навчитись визначати графічним методом розв’язок ЗЛП. Навчитись будувати багатокутник розв’язків, вектор-градієнт і лінію рівня для ЗЛП. Навчитись знаходити в багатокутнику розв’язків точки мінімуму і максимуму.
Час:	2 год.

2.1 Теоретичні відомості

Задача лінійного програмування складається у визначенні максимального (мінімального) значення функції

(2.1)

при умовах

(2.2)

Геометричне тлумачення цієї задачі міститься у визначенні такої точки багатокутника розв’язків, що обумовлюється системою (2.2), у якій цільова функція приймає максимальне (мінімальне) значення. У випадку ЗЛП можна розв’язати на площині за допомогою графічного методу.

Пошук розв’язку задачі лінійного програмування (2.1) – (2.2) на основі її геометричної інтерпретації включає наступні етапи:

1. Побудова прямих, рівняння яких отримують у результаті заміни в обмеженнях (2) знаків нерівностей на знак рівності.

2. Пошук напівплощин, що задаються кожним обмеженням задачі.

3. Пошук багатокутника розв’язків (області допущених значень).

4. Побудова вектора .

5. Побудова лінії рівня перпендикулярно до вектора-градієнта, (лінію рівня можна провести через точки , підбирається таким чином, щоб лінія рівня проходила через багатокутник розв’язків).

6. Якщо необхідно знайти максимальне значення цільової функції, лінія рівня пересувається в напрямку вектора 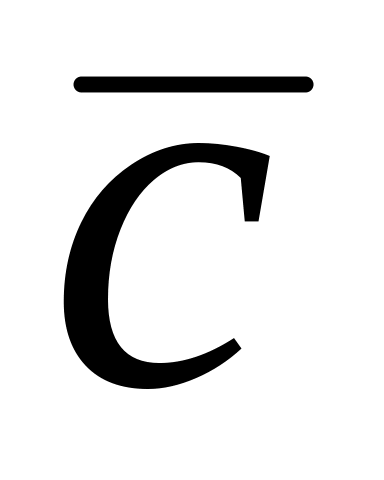до останньої загальної точки з багатокутником розв’язків.

Якщо необхідно знайти мінімальне значення цільової функції, лінія рівня пересувається в напрямку, протилежному напрямкові вектора до останньої загальної точки з багатокутником розв’язків.

2.2 Практична частина

2.2.1 Контрольний приклад

Задача

Знайти мінімальне і максимальне значення функції при умовах

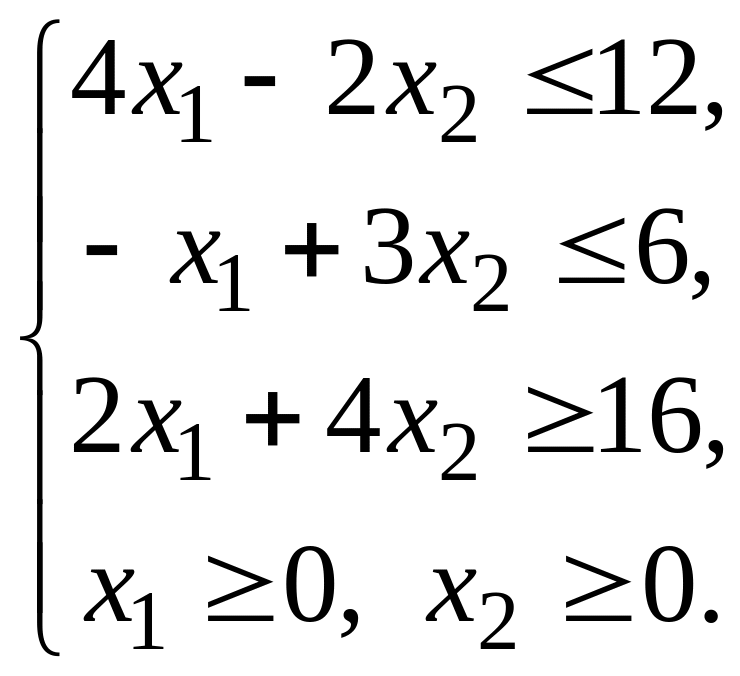
Розв’язання

__________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________

Висновок.

2.2.2 Самостійна робота

Використовуючи графічний метод розв’язання ЗЛП, знайти мінімальне (максимальне) значення цільової функції.

________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________В исновок

2.2.3 Контрольні питання

1 В чому полягає задача лінійного програмування?

2 В чому міститься геометрична інтерпретація ЗЛП?

3 Які основні етапи графічного методу пошуку розв’язку ЗЛП?

4 Як визначити розв’язок задачі лінійного програмування?

5 Які можливі варіанти ОДР?