Міністерство аграрної політики україни таврійський державний агротехнологічний університет
Факультет «Інженерії та комп’ютерних технологій»
Кафедра Прикладної геометрії і інформаційних технологій
проектування ім. В.М. Найдиша
Математичні методи дослідження операцій
РОБОЧИЙ ЗОШИТ
(частина І)
для виконання практичних занять студентами факультету ІКТ
спеціальності 6.050101 «Інформаційні технології проектування»
ОКР «Бакалавр»
Варіант |
|
Студент: |
|
Група: |
|
Викладач: |
|
Мелітополь
2010
Розробили: д.т.н., проф. Малкіна В.М., ас. Зінов’єва О.Г.
Рецензент: д.т.н., проф. Єремєєв В.С.
Розглянуто і схвалено на засіданні кафедри
«_____» ___________________20___р. Протокол № _____
Рекомендовано до друку методичною комісією факультету ІКТ
«_____» __________________ 20___р.. Протокол № _____
ЗМІСТ
МІНІСТЕРСТВО АГРАРНОЇ ПОЛІТИКИ УКРАЇНИ 1
1 ПРАКТИЧНЕ ЗАНЯТТЯ № 1 5
4 ПРАКТИЧНЕ ЗАНЯТТЯ №4 24
5 Практичне заняття № 5 34
Двоїстий симплекс-метод 34
Висновок 37
Висновок 39
7 Практичне заняття № 7 47
Транспортна задача 47
Варіанти для самостійної роботи №1: 56
79
79
79
79
ВСТУП
Робочий зошит призначений для виконання практичних занять з дисципліни «Математичні методи дослідження операцій» студентами факультету Інженерії і комп’ютерних технологій денної форми навчання спеціальності 6.050101.
Метою даного робочого зошиту є закріплення студентами вивченого теоретичного матеріалу і придбання практичних навичок для розв’язання задач лінійного програмування.
Методичні вказівки складені з врахуванням того, що студенти попередньо засвоїли теоретичний матеріал, наведений в літературі.
Для кожного практичного заняття наведено стислий опис теоретичних відомостей, варіанти для самостійного розв’язання.
Виконавши вказівки по заповненню робочого зошиту і заповнивши його, студенти здобувають навички по розв’язанню задач лінійного програмування, давати інтерпретацію отриманим розв’язкам.
1 Практичне заняття № 1
Тема: |
Постановка задачі лінійного програмування (ЗЛП) і побудова математичних моделей |
Мета: |
|
Час: |
2 год. |
1.1 Теоретичні відомості
Загальною задачею ЛП називається задача, що складається у визначенні максимального (мінімального) значення функції
,
(1.1)
при умовах
(1.2) (1.3)
де
– задані постійні величини.
Функція (1.1) називається цільовою функцією задачі (1.1) – (1.3), а умови(1.2) – (1.3) – обмеженнями даної задачі.
Стандартною задачею ЛП називається задача, що складається у визначенні максимального значення функції (1) при виконанні умов
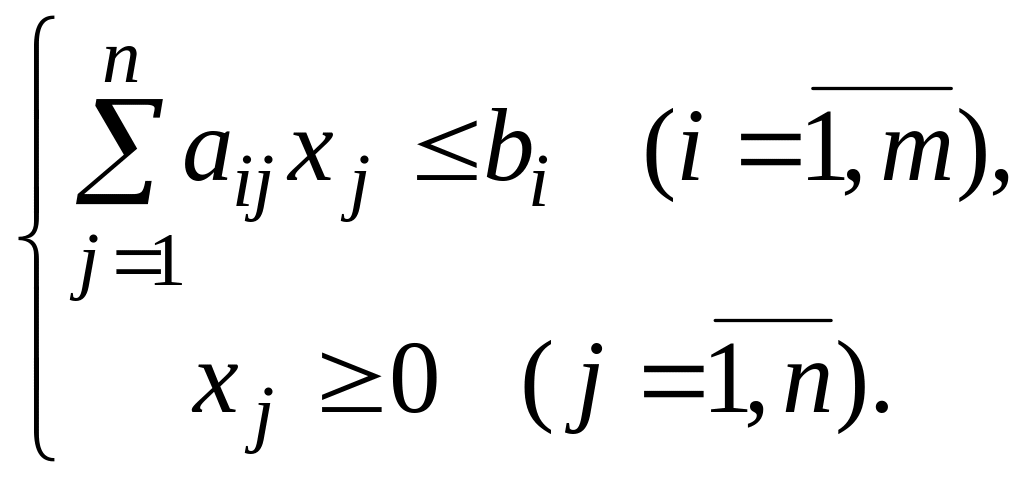
Канонічною задачею ЛП називається задача, що складається у визначенні максимального значення функції (1) при виконанні умов
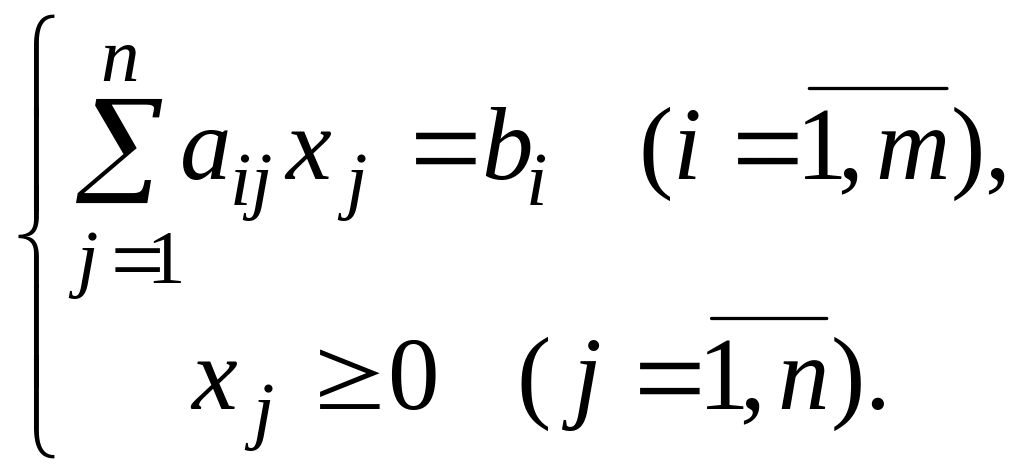
Математична постановка екстремальних задач складається у визначенні найбільшого або найменшого значення цільової функції (1.1) при заданій системі обмежень (1.2) – (1.3).
Для
того, щоб записати ЗЛП у канонічному
виді, потрібно перейти від обмежень-нерівностей
до обмежень-рівностей. Цей перехід
здійснюється введенням додаткових
ненегативних змінних, кількість яких
дорівнює кількості обмежень задачі.
При цьому до лівих частин кожного з
нерівностей виду «
» відповідна додаткова змінна додається,
а з лівих частин кожного з нерівностей
виду «
» віднімається. У першому випадку
додаткова змінна – невикористана
частина ресурсу, а в другому – міра
перевищення потреби.
Щоб перейти від пошуку мінімального значення задачі до пошуку максимального, необхідно знаки коефіцієнтів у цільовій функції замінити на протилежні.