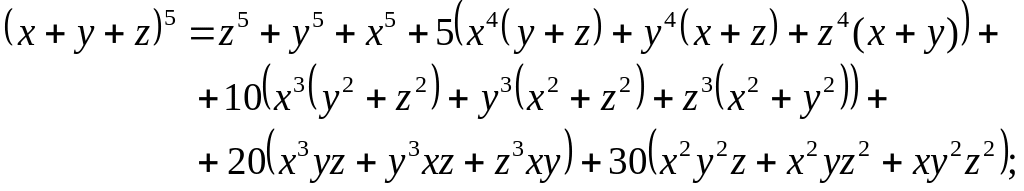Короткі теоретичні відомості до теми

“Біном Ньютона. Поліноміальні коефіцієнти. Рекурентні рівняння”

Біномом Ньютона називається вираз

(9)

або

,

(10)

Зазначимо, що іноді співвідношення (9) подається у вигляді:

(11)

Нагадаємо деякі з властивостей біноміальних коефіцієнтів :

1. .

2. .

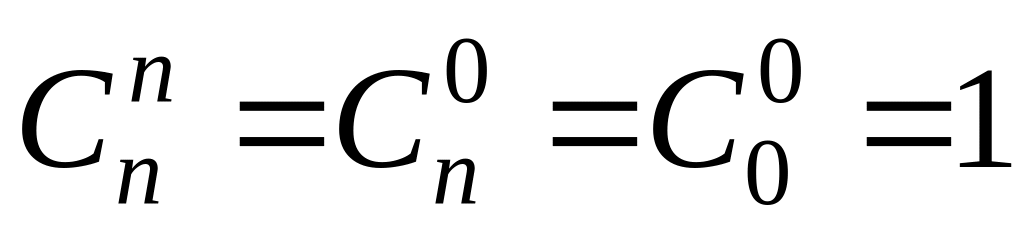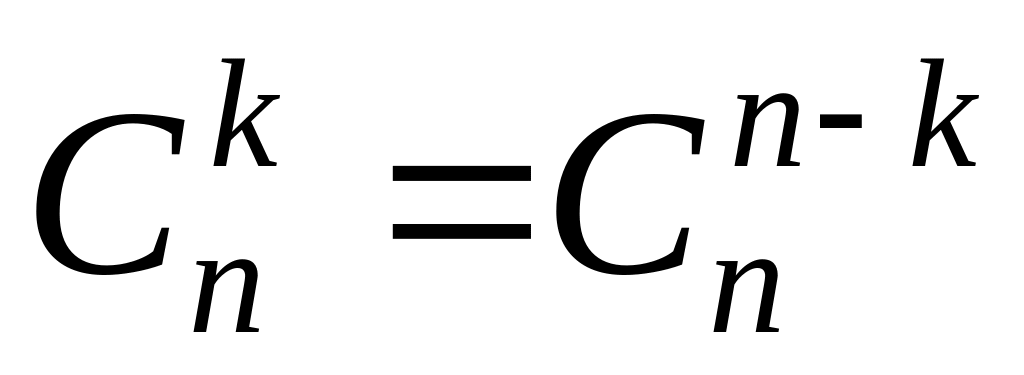3. Властивість Паскаля. .

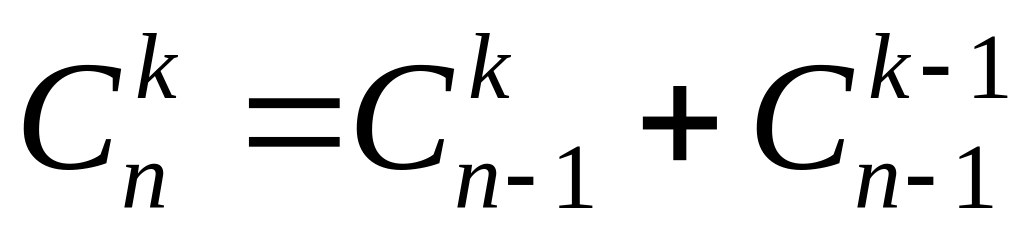Проілюструємо використанням біному Н’ютона та поліноміальної формули (6) для розв'язування задач.

Задача 1.

Довести тотожність

1. ;

2. ;

3. .

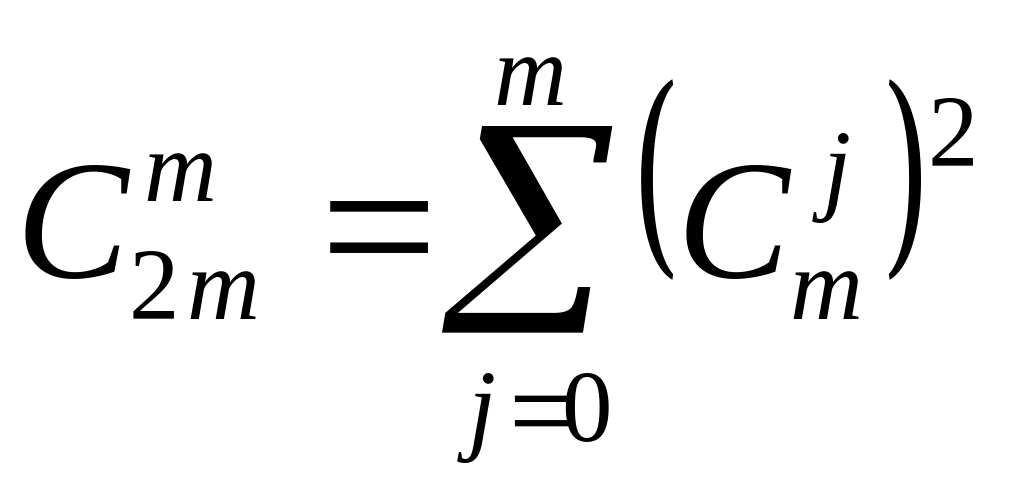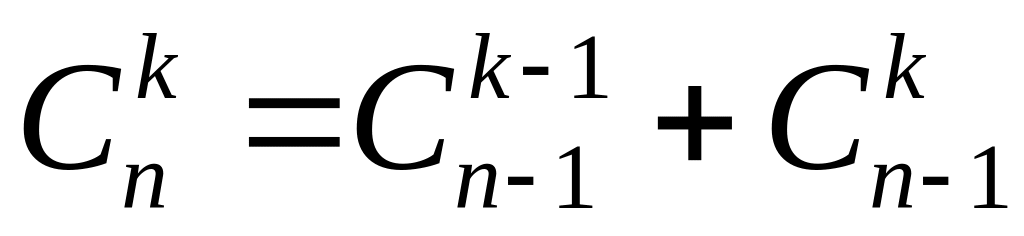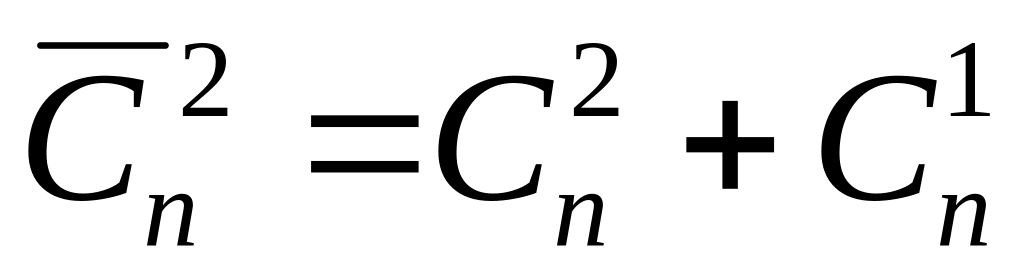Розв'язування. Для доведення тотожностей будемо використовувати біном Ньютона (9), властивості біноміальних коефіцієнтів, формули числа комбінацій з повтореннями (4) та без повторень (3) і їх властивості

А) 1-ий спосіб. Для доведення тотожності використаємо формулу біному Ньютона у вигляді (11): та властивості многочленів. Ліву частину цього співвідношення за властивістю степенів подамо у вигляді добутку двох однакових співмножників, кожен з яких розвинемо за формулою (10):

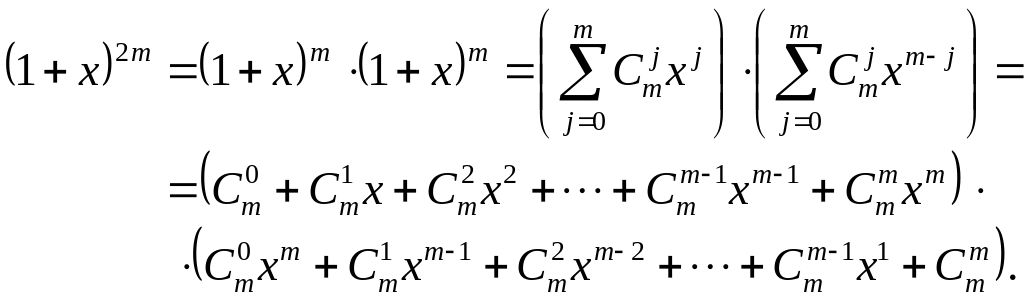
Розкриємо дужки та зберемо подібні члени відносно степенів змінної .

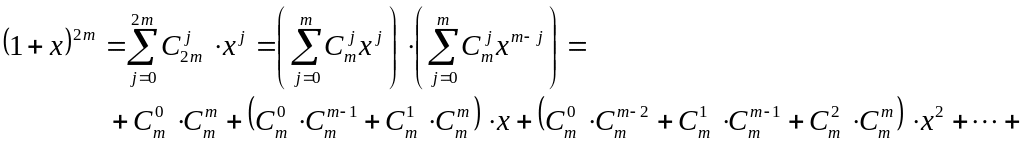
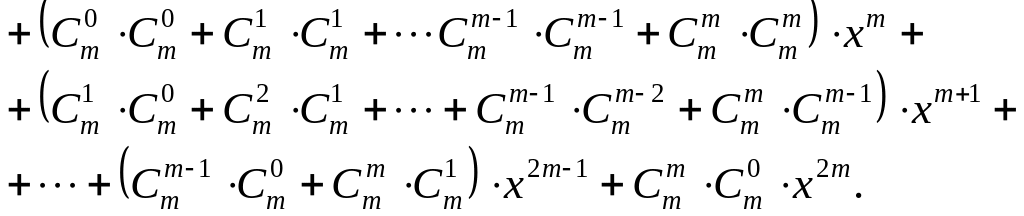
За властивістю рівності двох многочленів прирівняємо коефіцієнти при у лівій та правій частинах отриманого співвідношення:

та отримаємо підтвердження, що розглядуване співвідношення є тотожністю.

.

2-ий спосіб. Нагадаємо відому властивість біноміальних коефіцієнтів

.

Якщо в цю формулу покласти та використати властивість ,

то отримаємо рівність, яку необхідно було довести.

Б) Розглянемо кожну складову співвідношення за формулою сполук без повторень (3)

,

Запишемо праву частину розглядуваної рівності згідно цих формул:

.

Зведемо дроби у правій частині до спільного знаменника, враховуючи властивість числа перестановок (факторіала): , та отримаємо:

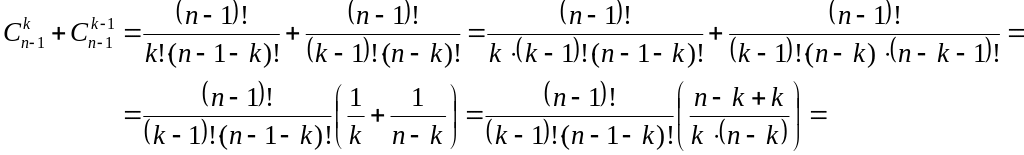
Отже, після виконання перетворень над правою частиною розглядуваного співвідношення, було отримано його ліву частину. Тотожність доведено.

В) Запишемо ліву частину заданої рівності за формулою сполук із повтореннями (4):

.

Запишемо праву частину рівності за формулою сполук без повторень (3) та винесемо за дужки спільні множники з чисельників та знаменників обидвох доданків, отримаємо аналогічне співвідношення:

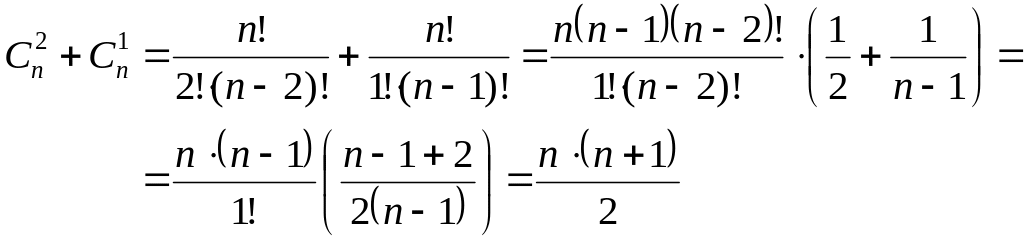
Оскільки ліва та права частини заданої рівності були зведені до однакового виразу, можемо зробити висновок про їх еквівалентність, тобто зазначити, що тотожність доведено

Відповідь: за властивостями бінома Ньютона та числа сполук доведено виконання тотожностей.

Задача 2.

Знайти значення суми:

1. ;

2. ;

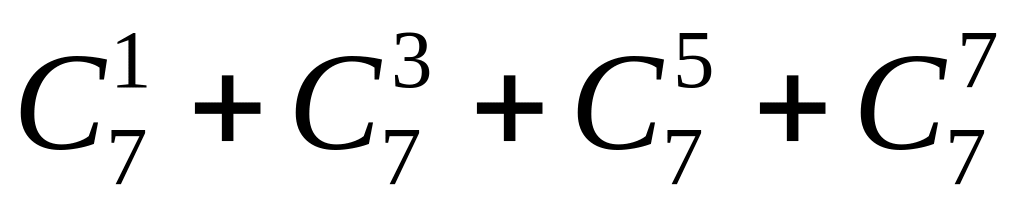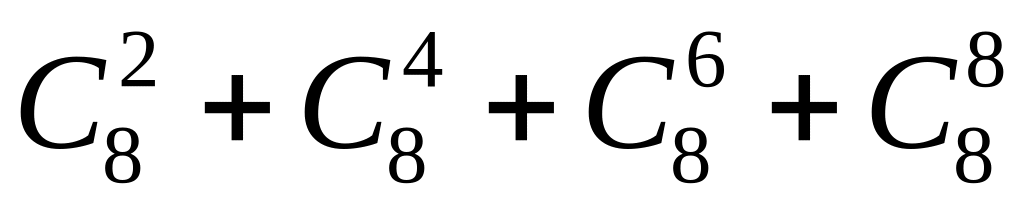Розв'язування.

А) 1-ий спосіб. Обчислимо значення суми , безпосередньо використовуючи формулу сполук без повторень (3):

.

2-ий спосіб. Обчислимо значення розглядуваної суми , використовуючи властивості сум біноміальних коефіцієнтів:

, , .

Згідно властивості суми непарних членів бінома Ньютона: — отримаємо значення .

Б) 1-ий спосіб.

.

2-ий спосіб . Використовуючи властивість біноміальних коефіцієнтів, розглянуту у пункті А, – значення суми парних біноміальних коефіцієнтів , – знайдемо шукане значення:

Відповідь: значення заданих сум є такими: А) ; Б) .

Задача  3.

Обчислити коефіцієнти многочлена:

А) ;

Б) .

Розв'язування. Розв'язання розглядуваних завдань ґрунтуватиметься на формулі (9).

А) Здійснимо заміну параметра а на у формулі бінома Ньютона, тоді

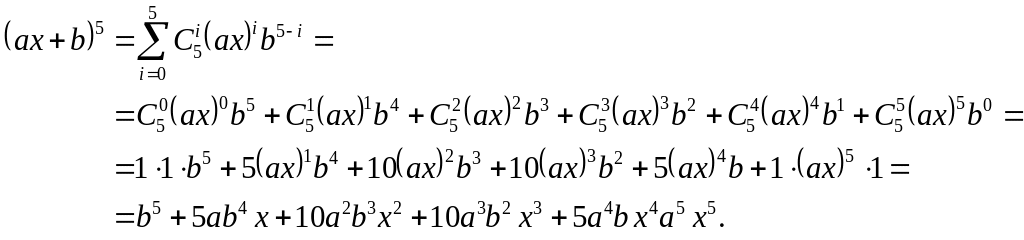
Таким чином, коефіцієнти многочлена будуть наступними:

Б) 1-ий спосіб. Застосовуючи формулу бінома Ньютона виду (9), знайдемо коефіцієнти многочлена 5-го степеня від трьох змінних , ввівши такі позначення: , .

Тоді отримаємо:

Кожен вираз у дужках розкриємо, використовуючи формулу (9) для кожного значення степеня , та отримаємо

;

;

;

.

Підставимо отримані вирази у співвідношення для :

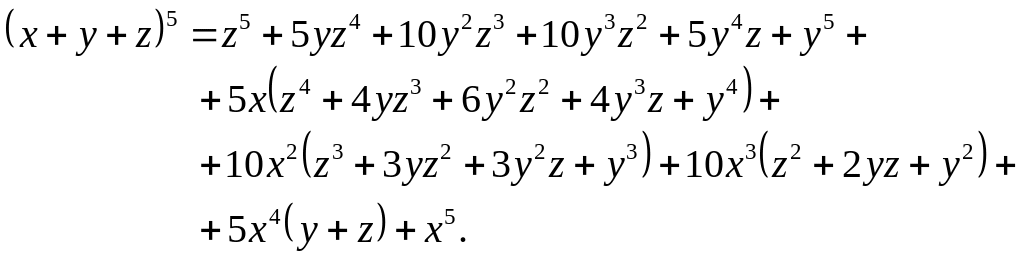
Тепер зведемо подібні члени з однаковими коефіцієнтами, розкривши дужки, та отримаємо

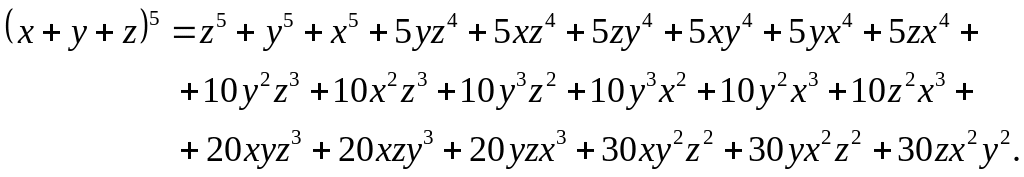
Отже,

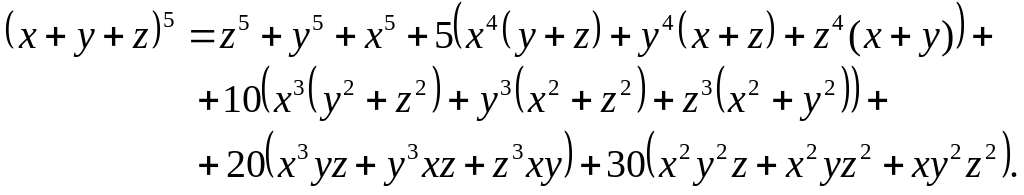
2-ий спосіб. Використаємо комбінаторні об'єкти для канонічного представлення многочлена k степеня від n змінних: число перестановок з повтореннями та число комбінацій з повтореннями.

Загальна кількість членів, які буде містити отриманий многочлен після розкриття дужок та зведення подібних членів, буде дорівнювати

.

Розглядуваний многочлен залежить від 3-х змінних, тоді в нашому випадку та — степінь многочлена. Тому загальна кількість членів (доданків), які буде містити результуючий многочлен становитиме . Якщо підрахувати число доданків, які ми отримали в результуючому виразі для за першим способом, то отримаємо те саме значення 21.

Коефіцієнти такого многочлена можна отримати за допомогою поліно­міальної формули (6), згідно якої у заданому прикладі а степінь змінної , степінь змінної , степінь змінної у кожному з доданків формули.

Тоді за співвідношенням (6) коефіцієнт, що стоїть при , буде дорівнювати . Аналогічними будуть коефіцієнти при та .

Обчислимо коефіцієнт, що стоїть біля члену . За вищевказаною формулою він буде дорівнювати . Аналогічно знаходяться коефіцієнти для , , , та .

Визначимо коефіцієнт, що стоїть біля виразу , за формулою (6): . Таке ж значення коефіцієнта, що стоїть при , , , та .

Коефіцієнт, що стоїть при , дорівнює відповідно , як і аналогічні коефіцієнти при та .

Коефіцієнт при члені визначимо як . Таке ж значення коефіцієнтів, що стоять при та .

Тоді многочлен можемо записати у вигляді:

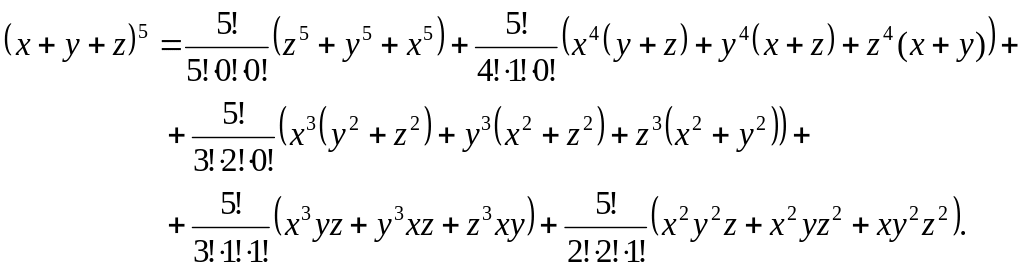
Таким чином, коефіцієнти, обчислені за поліноміальною формулою, повністю співпадають із коефіцієнтами, визначеними за допомогою першого способу.

Відповідь: задані многочлени матимуть таке розвинення:

Задача 4.

У заданому виразі розкрили дужки та звели подібні члени. Скільки членів буде містити многочлен та яким буде коефіцієнт, що стоятиме при доданку у цьому многочлені?

Розв'язування. Загальна кількість членів, які входитимуть у многочлен го степеня від змінних після розкриття дужок та зведення подібних членів буде дорівнювати числу сполук із повтореннями, що визначається формулою (4)

Коефіцієнти такого многочленна можна отримати за допомогою полі­номіальної формули (6), де степінь при і-ій змінній у відповідному члені многочлена.

У многочлені число змінних 3, а його степінь 9: , . Загальна кількість членів, які буде містити заданий многочлен після розкриття дужок та зведення подібних членів, буде становити

.

Коефіцієнт при члені дорівнюватиме .

Відповідь: кількість доданків дорінює 55, а значення коефіцієнта при відповідному членові — 1260.

Задача 5.

Скільки цілочисельних розв'язків мають наступні рівняння?

1. ;

2. .

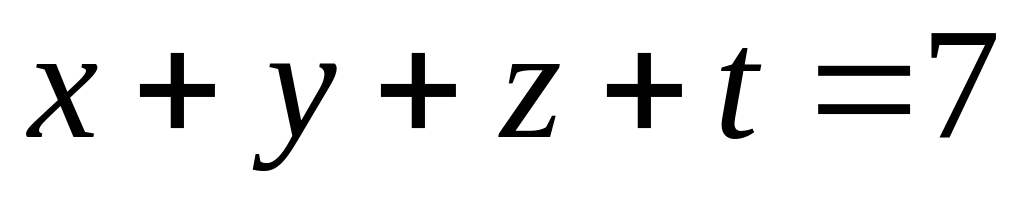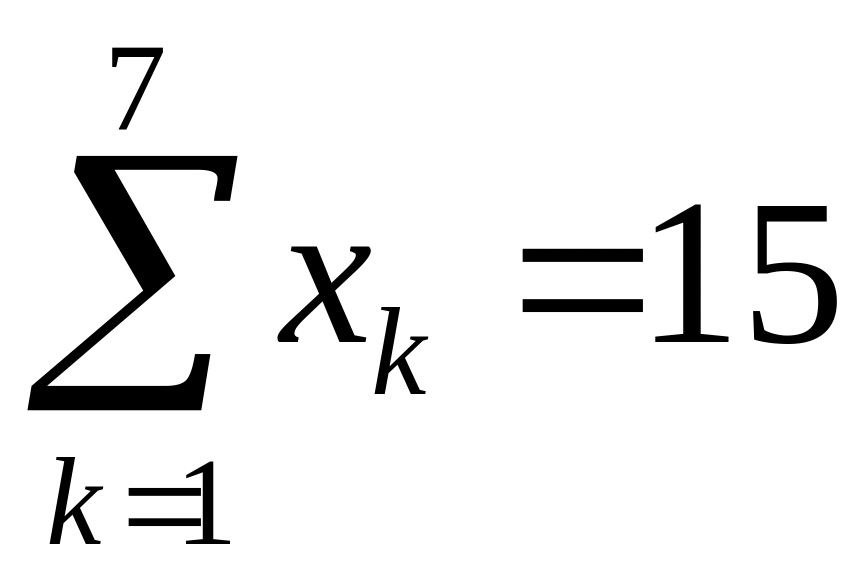Розв'язування. Загальна кількість цілочисельних невід'ємних розв'язків рівняння

, де ,

визначається за формулою числа сполук з повтореннями (4).

А) Задане рівняння залежить від чотирьох змінних ( ), кожна з яких може набувати цілочисельного невід'ємного значення від 0 до . Отже, загальне число таких розв’язків розглядуваного рівняння буде дорівнювати

.

Б) Лінійне рівняння , що залежить від семи змінних , має скінченну множину цілочисельних невід'ємних розв'язків, значення кожної з цих змінних не перевищує числа . Потужність цієї множини дорівнює загальній кількості цілочисельних розв'язків розглядуваного рівняння та буде визначатися за числом сполук із повтореннями:

.

Відповідь: кількість невід'ємних цілочисельних розв'язків відповідного рівняння становитиме А)120; Б) 54264.

Задача 6.

Знайти середній член розкладу виразу

.

Розв'язування У формулі бінома Ньютона покладемо , , , тоді заданий розклад матиме вигляд .

Для встановлення лічби доданків у розглядуваному співвідношенні використаємо відому формулу (4) числа комбінацій з повтореннями , що вкаже на 13 доданків. Отже, середній член розкладу матиме номер 7, і це буде член при (0..6) з коефіцієнтом . А сам член розкладу дорівнює

.

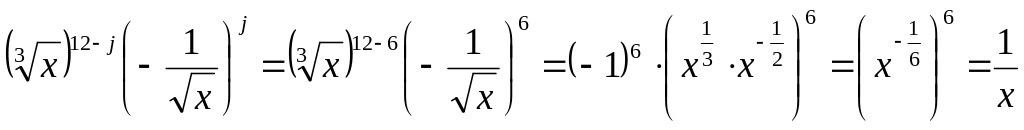Відповідь: середній член розкладу буде дорівнювати 924 .

Задача  7.

Знайти член розкладу бінома , який містить , якщо сума всіх його біноміальних коефіцієнтів дорівнює 128.

Розв'язування.

Згідно властивості суми всіх біноміальних коефіцієнтів , яку можна довести, поклавши у формулу бінома Ньютона значення , ця сума дорівнює . Тому, згідно з умовою завдання маємо, що , тобто , звідки . Отже, розглядуваний вираз є співвідношенням виду .

Для знаходження члена, який мітитиме , уведемо у формулі (9) такі позначення , для , й отримаємо вираз:

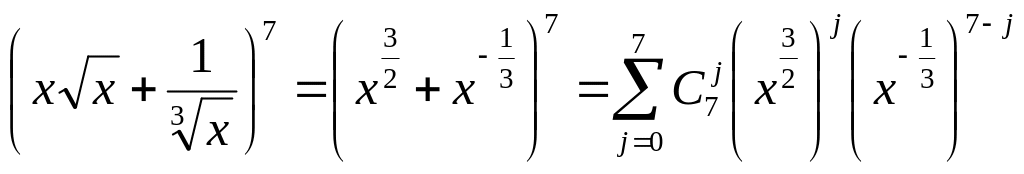
Запишемо загальний j-ий член такого розкладу: . Згідно умови він повинен містити . Тому виконаємо дії зі степенями, пам’ятаючи, що при множенні степенів з однаковими основами їх показники додаються — , а при піднесенні степеня до степеня їх показники перемножуються — . Звідки отримуємо , , значить . Розв’язуючи останнє рівняння

, ,

отримаємо значення .

Таким чином, член розкладу виразу , який містить , буде мати коефіцієнт, що дорівнює .

Зауважимо, що в силу симетрії біноміальних коефіцієнтів, такий же скаляр буде і при , але степеневий вираз буде інакшим: .

Відповідь: коефіцієнт розкладу , який містить дорівнює 35.

Задача 8.

Знайти загальний розв'язок заданих рекурентних рівнянь:

1. ;

2. .

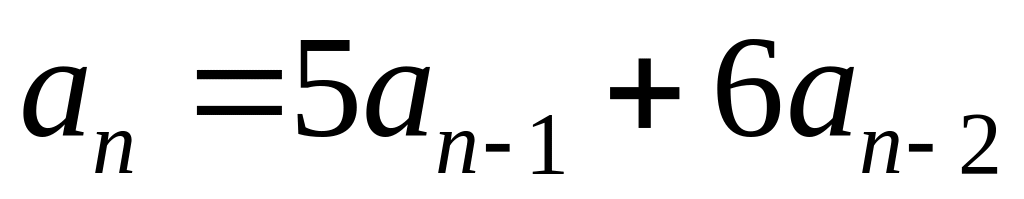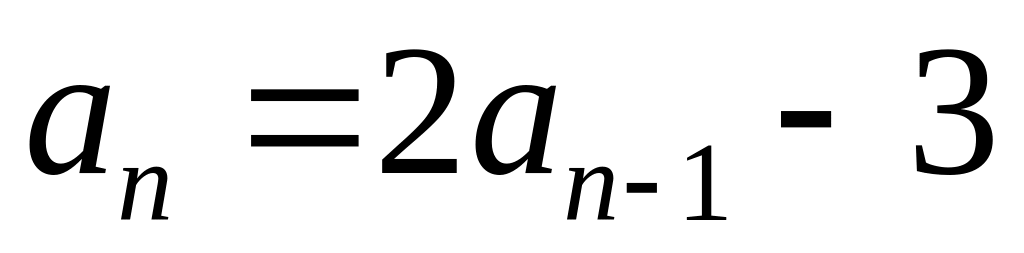Розв'язування.

Для знаходження загального розв'язку лінійного однорідного рекурентного рівняння використаємо метод характеристичного рівняння. Це характеристичне рівняння отримуємо з припущення, що розв'язком такого рівняння є вираз . Підставляємо цей вираз у рівняння, скорочуємо на спільний вираз, яким буде степінь числа , отримаємо многочлен відповідного степеня, який і буде характеристичним рівнянням.

А) Отже, покладемо у лінійне однорідне рекурентне рівняння співвідношення та отримаємо вираз . Скоротимо кожен з його членів на і тоді характеристичним рівнянням розглядуваного рекурентного буде рівняння вигляду , тобто, . Корені цього квадратного рівняння отримаємо за теоремою Вієта і будемо мати , . Оскільки корені дійсні різні, то загальний розв'язок лінійного однорідного рекурентного рівняння буде мати вигляд

,

де — невизначені константи, які залежать від початкових умов задачі.

Б) Рівняння є неоднорідним лінійним рівнянням першого порядку, оскільки кожен член рекурентного співвідношення залежить лише від одного попереднього члена, а також є вплив неоднорідності виду . За теоремою про структуру лінійного неоднорідного рівняння його розв'язок складається зі суми загального розв'язку відповідного однорідного рівняння та деякого частинного розв'язку неоднорідного рівняння, індукованого неоднорідністю :

.

Знайдемо загальний розв'язок однорідного рівняння . Його характеристичне рівняння матиме вигляд . Тоді загальний розв'язок відповідного однорідного рівняння першого порядку буде таким

.

Для знаходження частинного розв'язку розглядуваного рівняння з неоднорідністю використаємо метод підбору невизначених коефіцієнтів, враховуючи, що . Отже, , оскільки неоднорідність є константою. Значення цієї константи встановимо, підставляючи у неоднорідне рівняння, зауважуючи також, що має місце рівність .

Так як , то , тому .

Таким чином, .

Перевіримо, підставляючи загальний розв'язок неоднорідного рівняння у задане :

.

Ця рівність є тотожністю, бо .

Коефіцієнт залежить від початкових умов.

Відповідь: загальний розв'язок кожного рівняння відповідно буде таким:

1. ;

2. .

Задача 9.

Розв'язати рекурентні рівняння для заданих початкових умов.

1. , , ;

2. , .

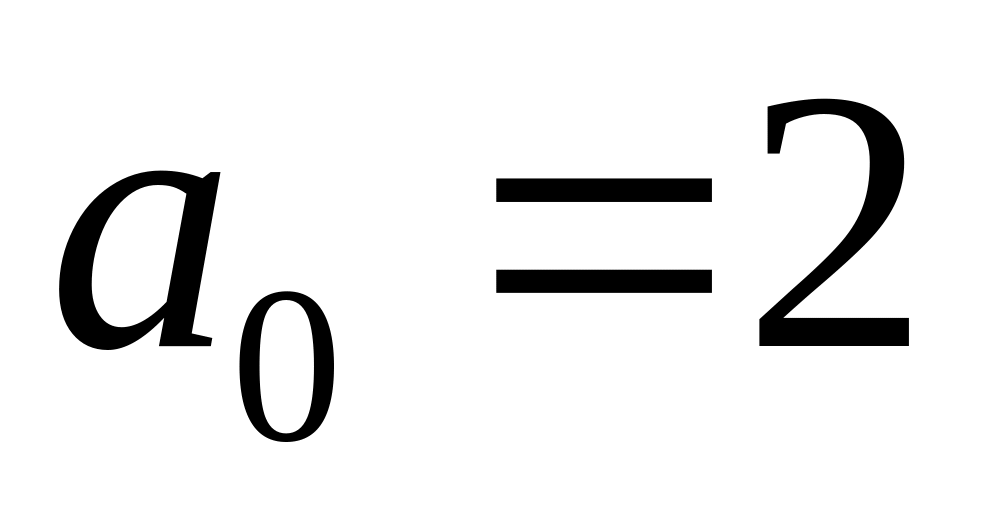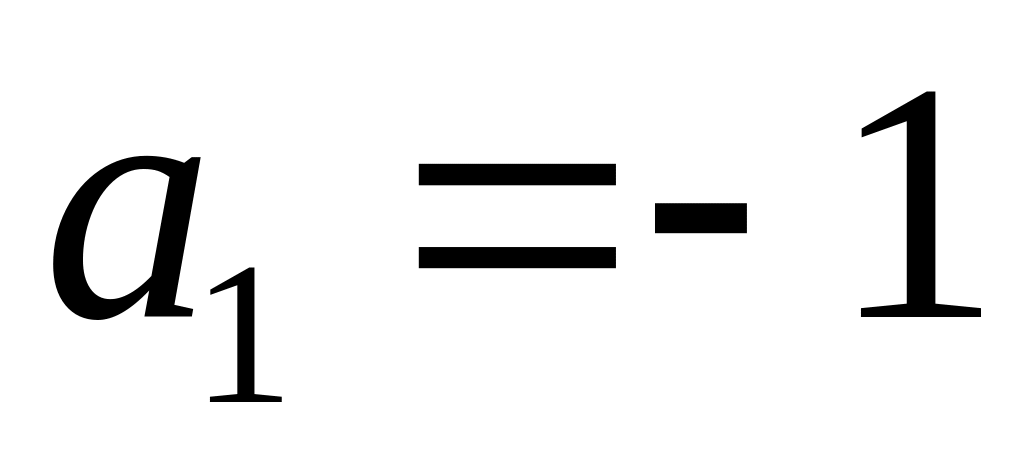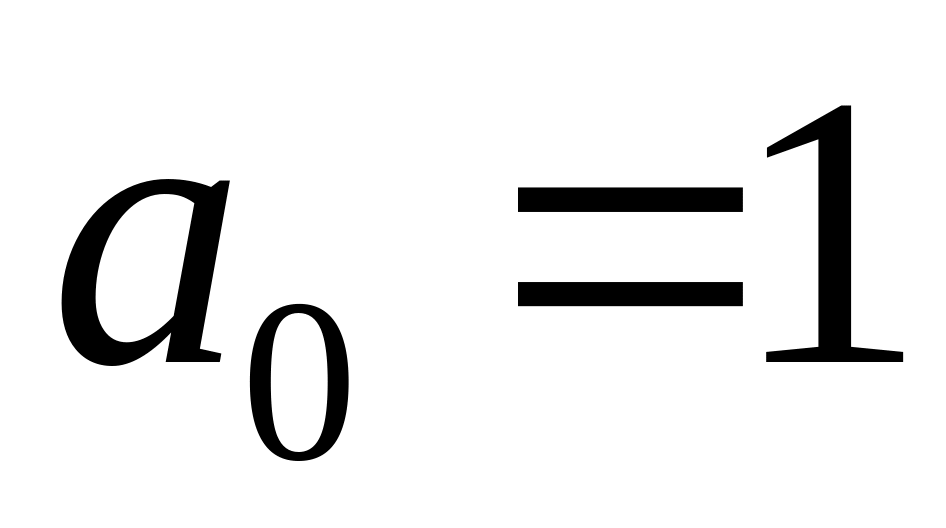Розв'язування.

Для знаходження розв'язку рекурентного рівняння зі заданими початковими умовами спершу слід знайти загальний розв'язок відповідного рекурентного рівняння, а тоді підставити початкові умови та встановити значення невизначених коефіцієнтів.

А) Загальний розв'язок рівняння , визначений у завданні А) задачі 8, має вигляд . Для знаходження невизначених коефіцієнтів використаємо відповідні початкові умови, покладаючи значення , :

Додамо обидва рівняння системи та отримаємо значення :

, отже . Далі з першого рівняння визначимо : . Отже, розв'язок рівняння , що задовольняє початкові умови , , має вигляд: .

Б) Загальний розв'язок неоднорідного рівняння має вигляд містить невизначений параметр . Для його встановлення використаємо задану початкову умову , поклавши вказане значення у вираз загального розв'язку: . Отже, . Тоді шуканий розв'язок матиме вигляд:

Відповідь: розв'язки рекурентних рівнянь, що задовольняють вказані початкові умови, є наступними: А) ; Б) .

Завдання для самостійної позаавдиторної роботи студентів

Завдання 1. Довести тотожності.

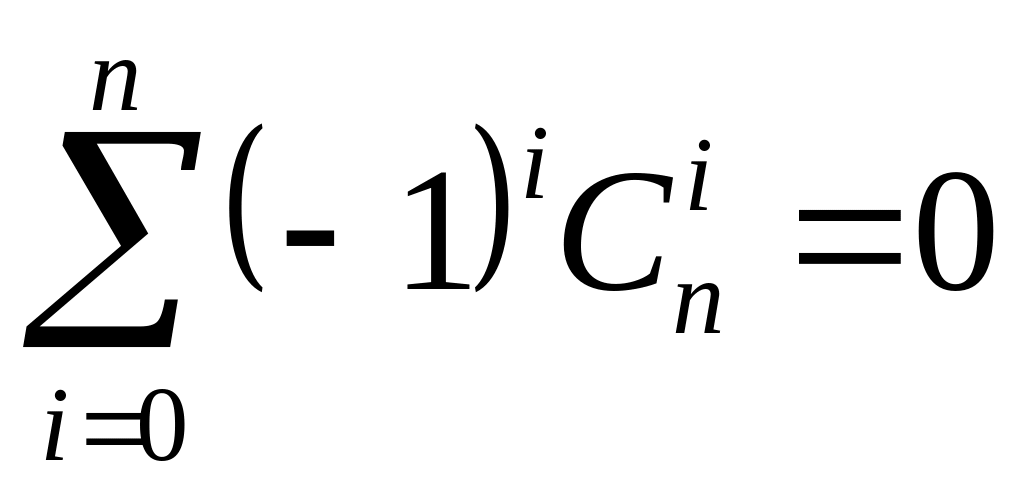1. змінити;

2. ;

3. ;

4. ;

5. ;

6. .

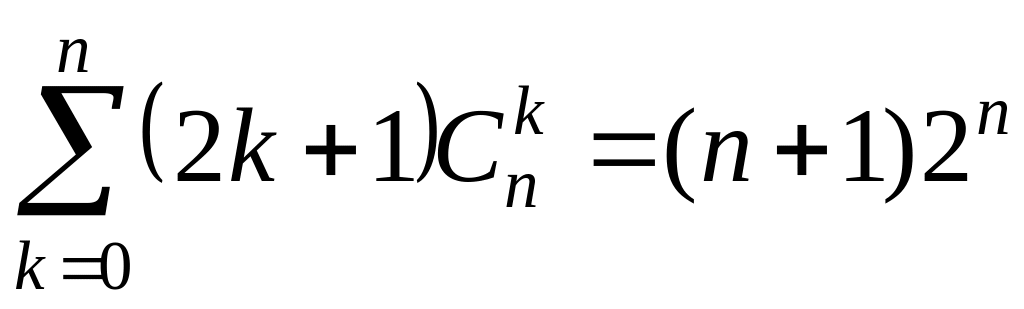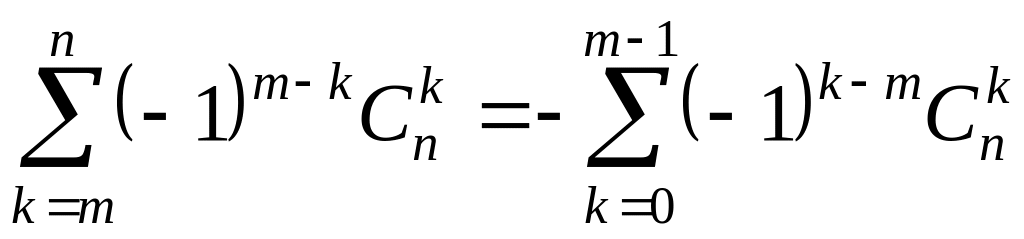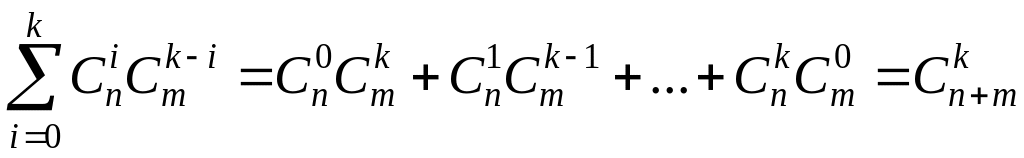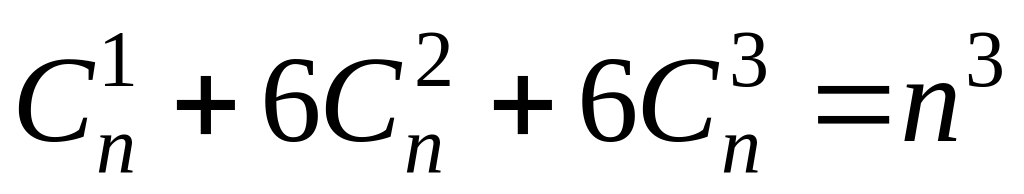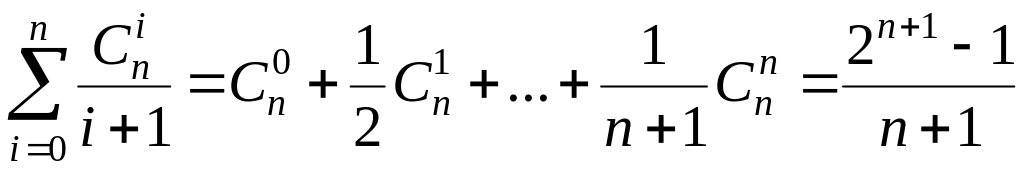Завдання 2. Чому дорівнює вказана сума?

1. ;

2. ;

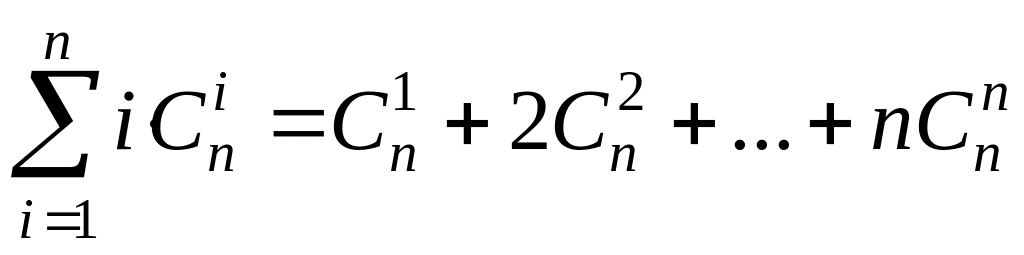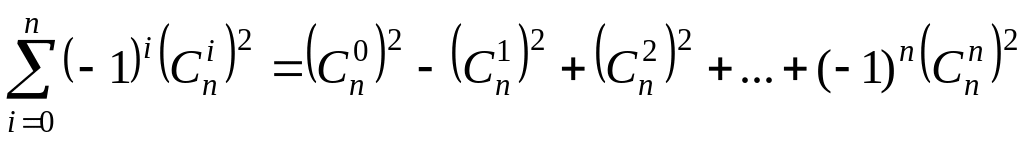3. для парних значень : ;

4. ;

5. .

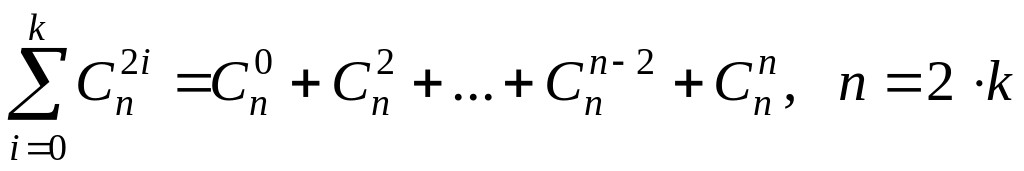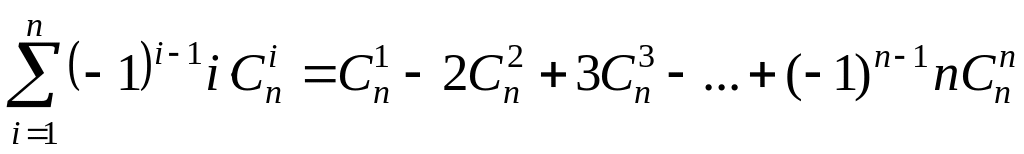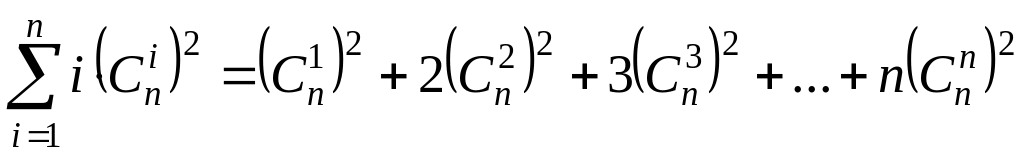Завдання 3. Обчислити коефіцієнти многочлена:

1. ;

2. ;

3. ;

4. .

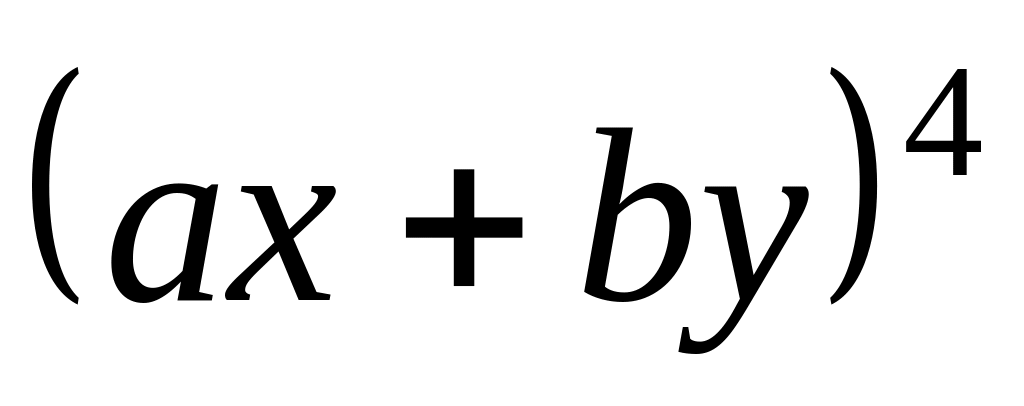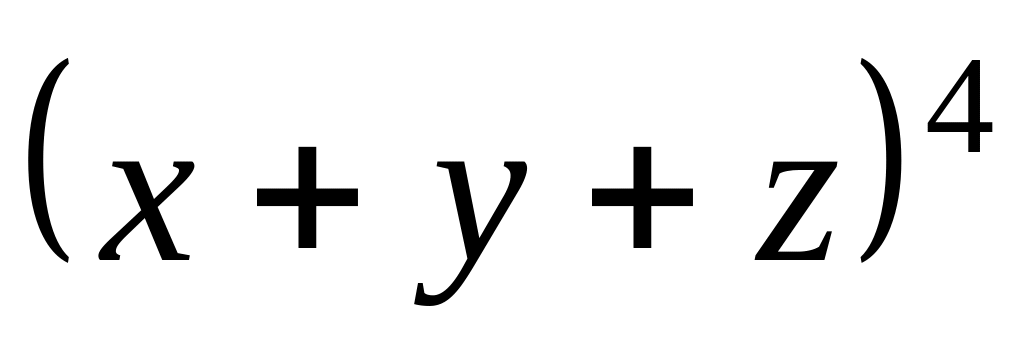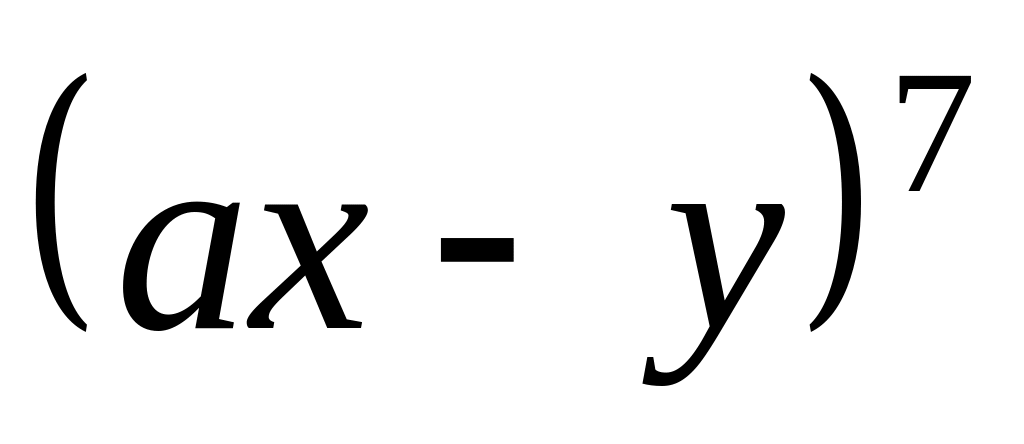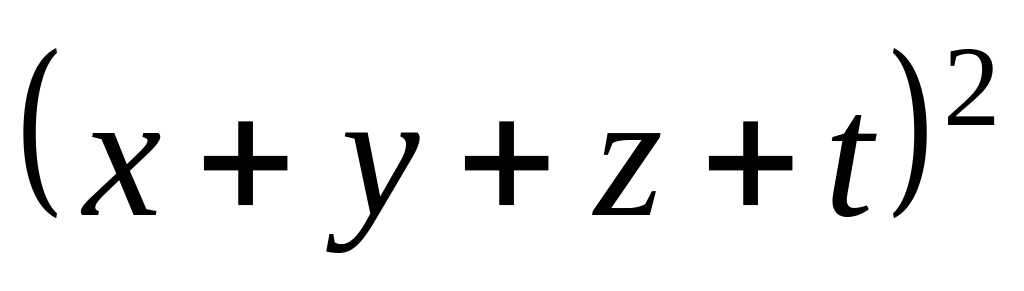Завдання 4. Скільки доданків буде містити отриманий многочлен після розкриття дужок та зведення подібних членів у виразах?

1. ;

2. ;

3. ;

4. .

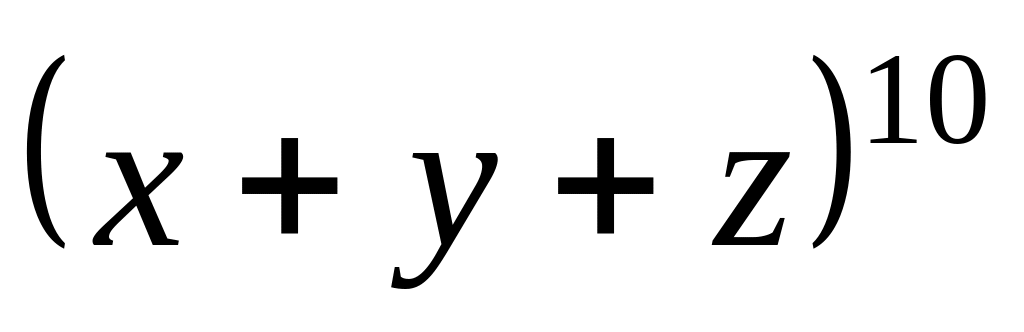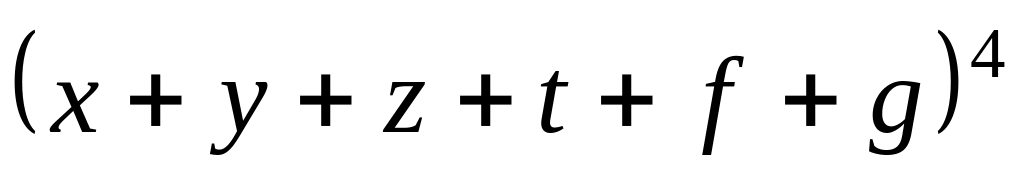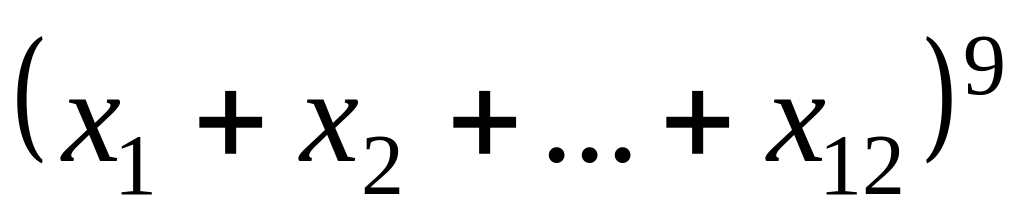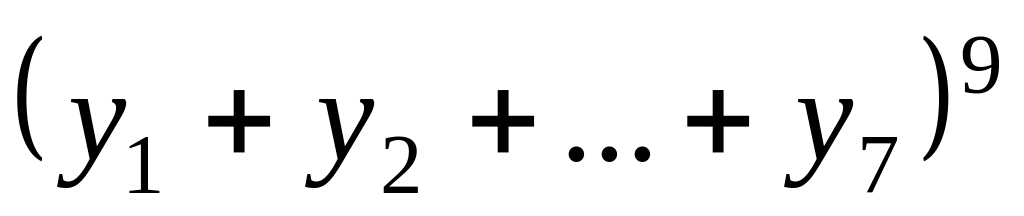Завдання 5. У заданому виразі розкрили дужки та звели подібні члени. Скільки різних доданків буде містити отриманий многочлен та який коефі­цієнт буде стояти при заданому доданку в отриманому виразі?

1. , ;

2. , ;

3. , ;

4. , .

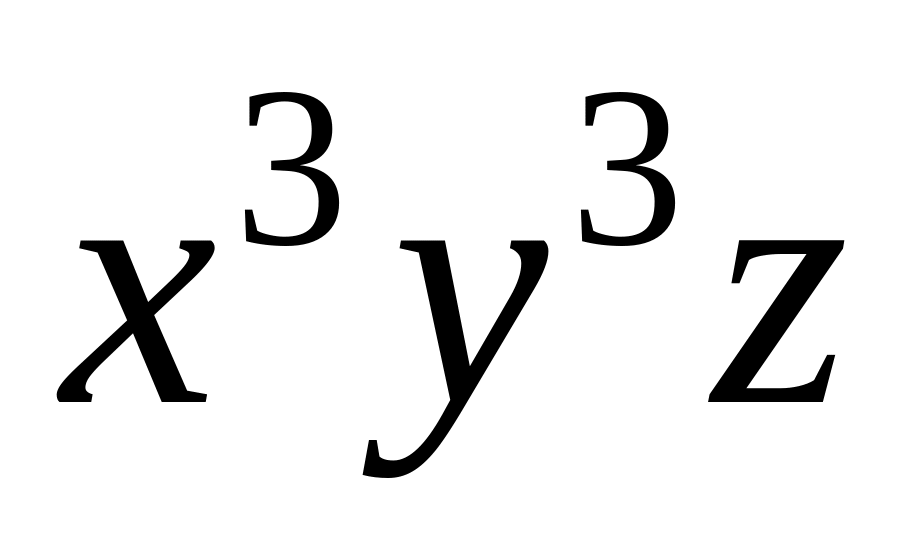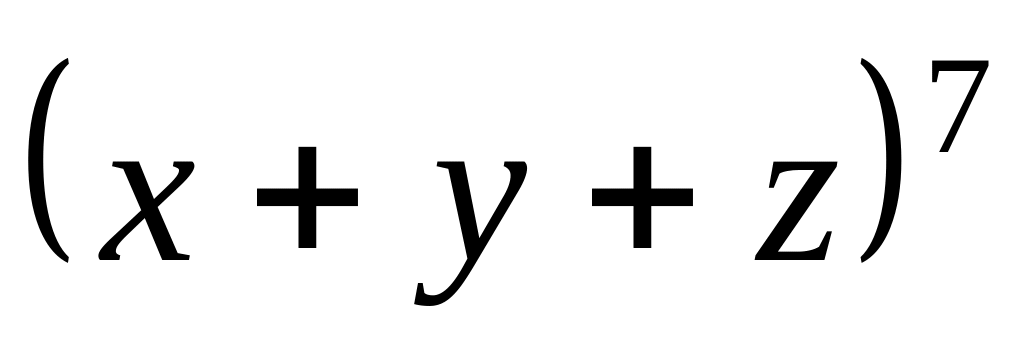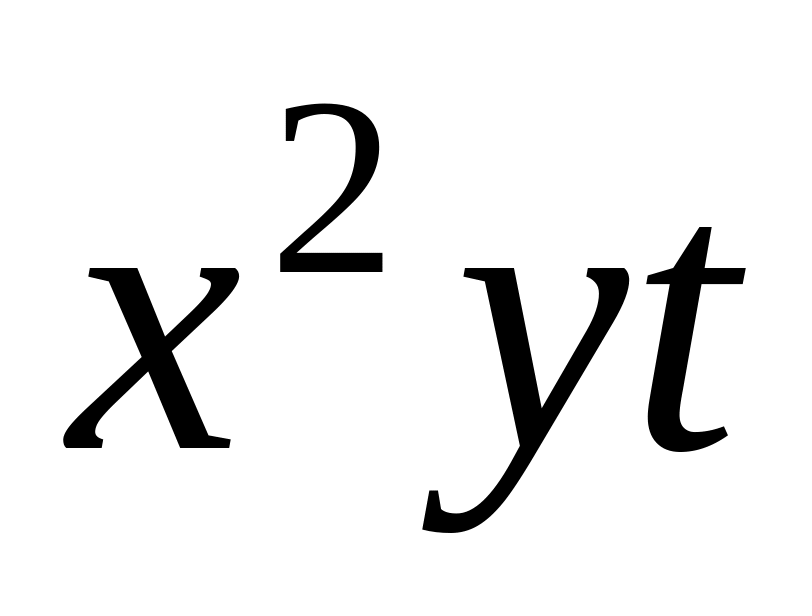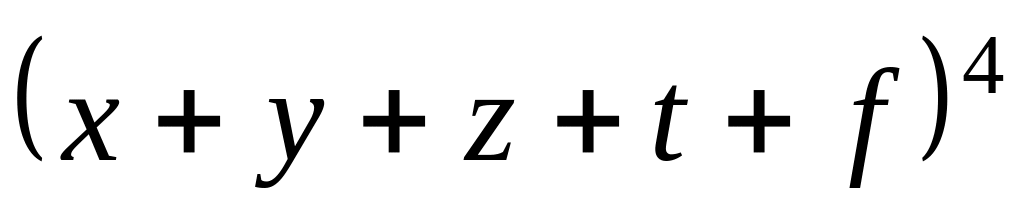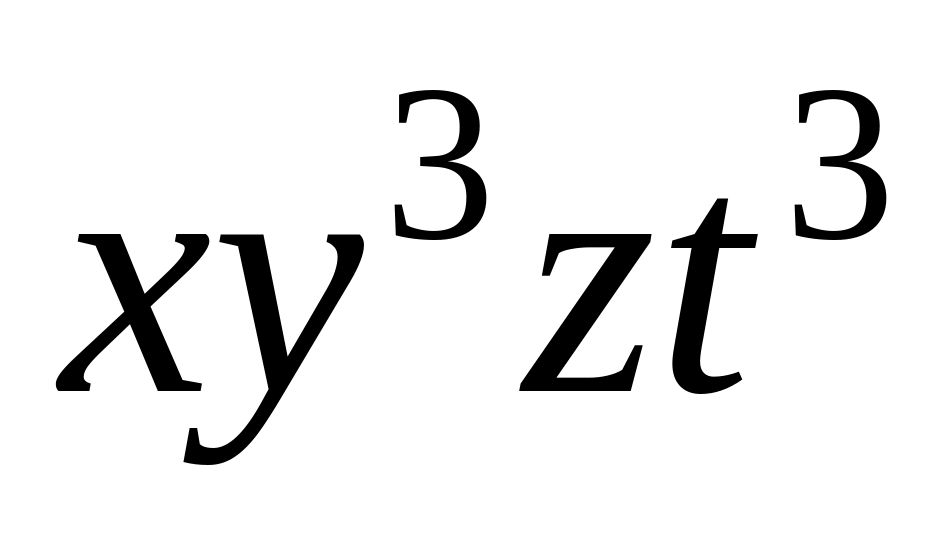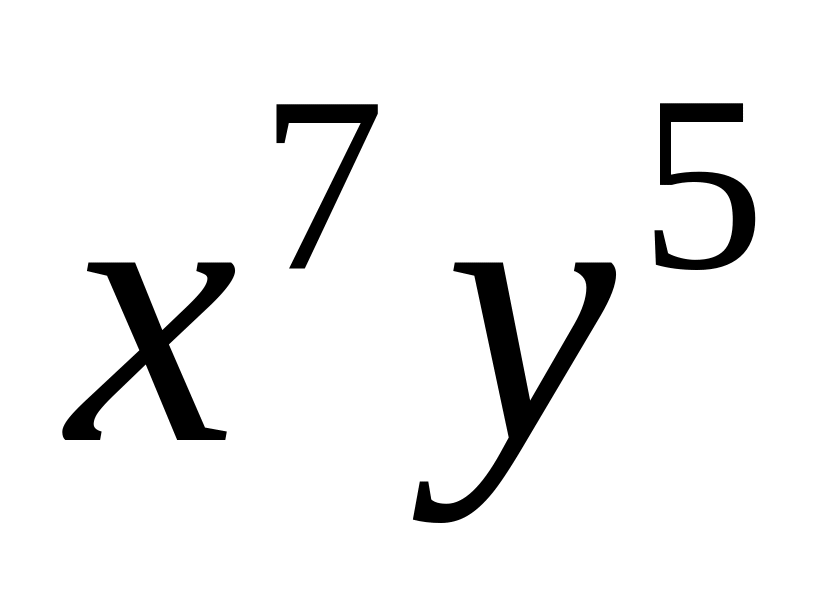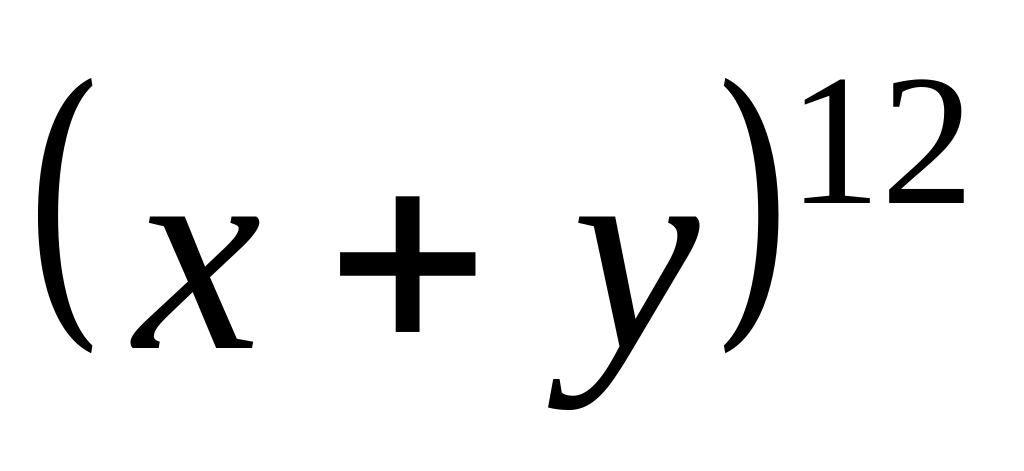Завдання 6. Скільки цілочисельних невід'ємних розв'язків мають наступні рівняння?

1. ;

2. ;

3. ;

4. .

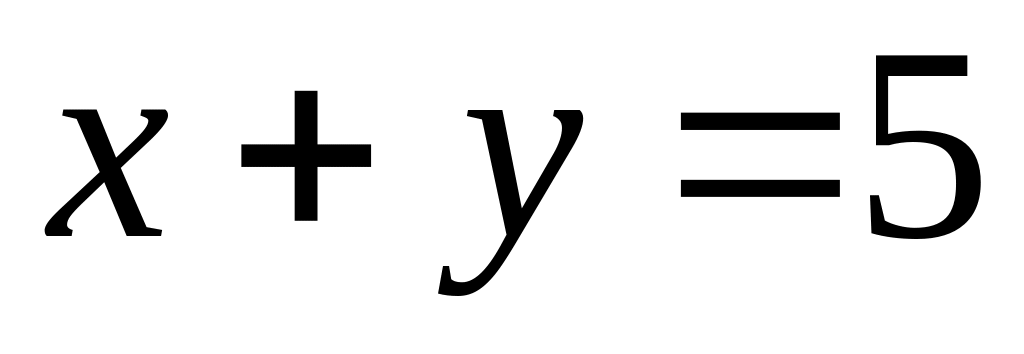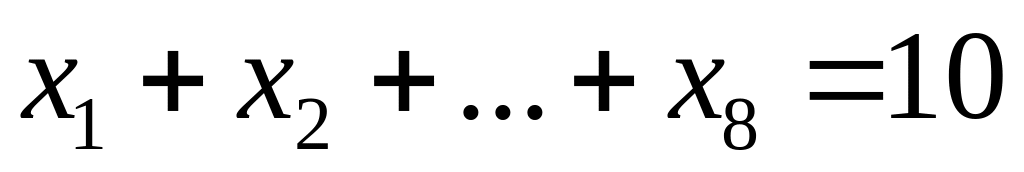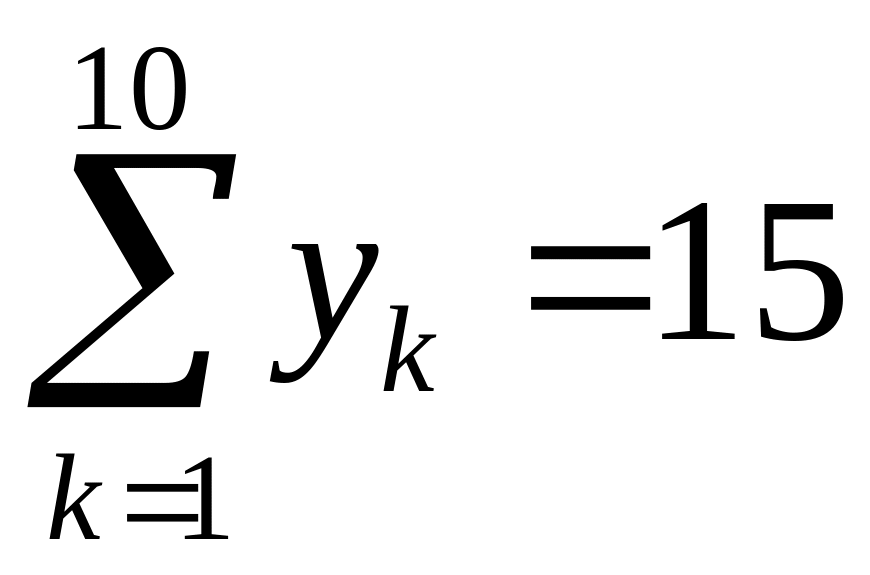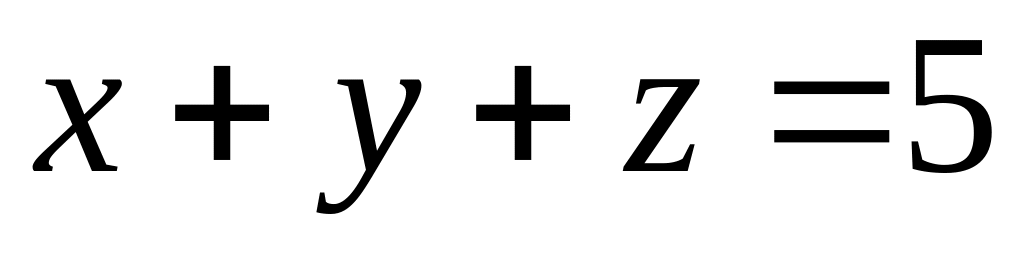Завдання 7. Знайти показник степеня бінома , якщо біноміальний коефіцієнт четвертого члена розкладу дорівнює 120.

Завдання 8. Знайти значення показника у розкладі бінома , якщо біноміальні коефіцієнти п’ятого і дев’ятого членів рівні між собою.

Завдання 9. У розкладі степеня бінома знайти доданок, що містить:

	;		;
	;		.

Завдання 10. У розкладі знайти вільний член, тобто доданок, який не містить .

Завдання 11. Знайти загальний розв'язок заданих рекурентних рівнянь:

1. ;

2. ;

3. ;

4. ;

5. .

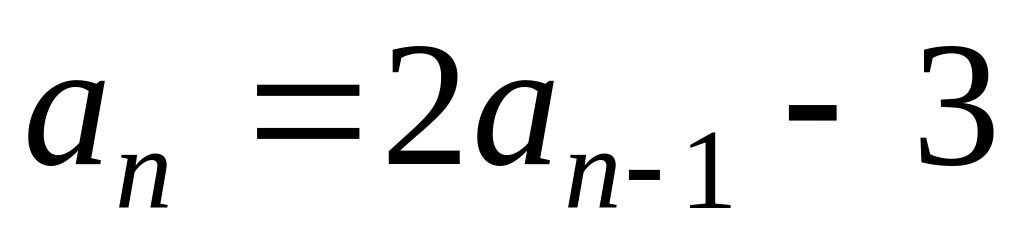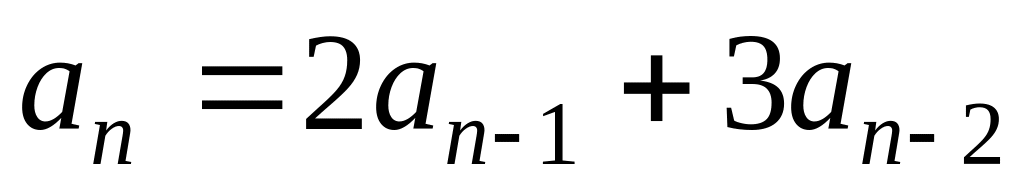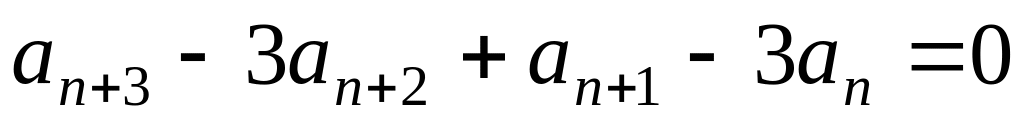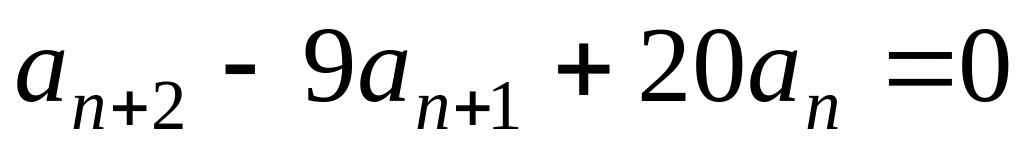Завдання 12. Розв'язати рекурентні рівняння.

1. , ;

2. , , ;

3. , , , ;

4. , , ;

5. , , , .

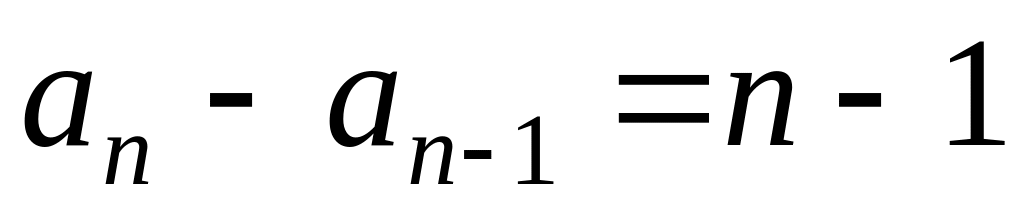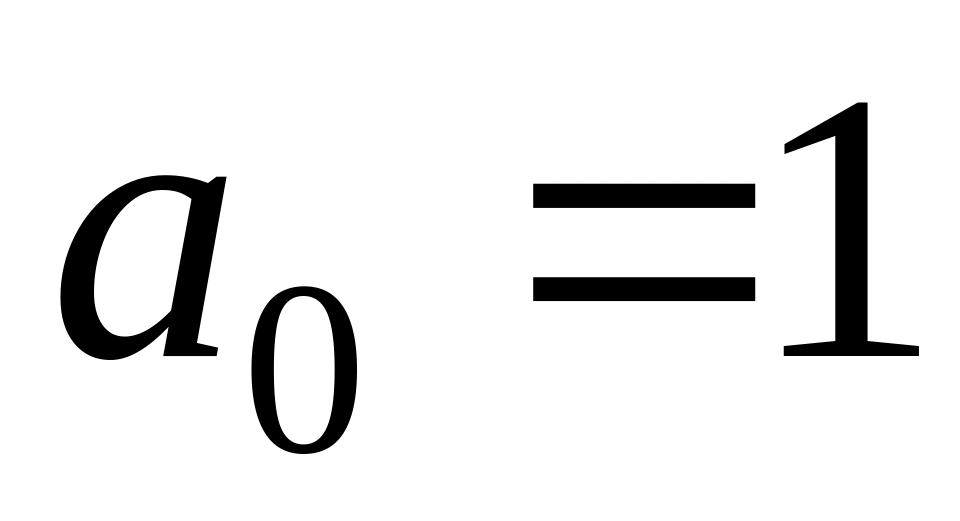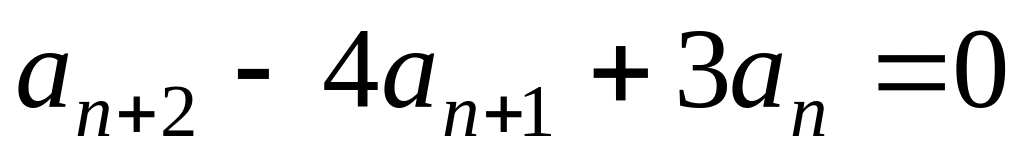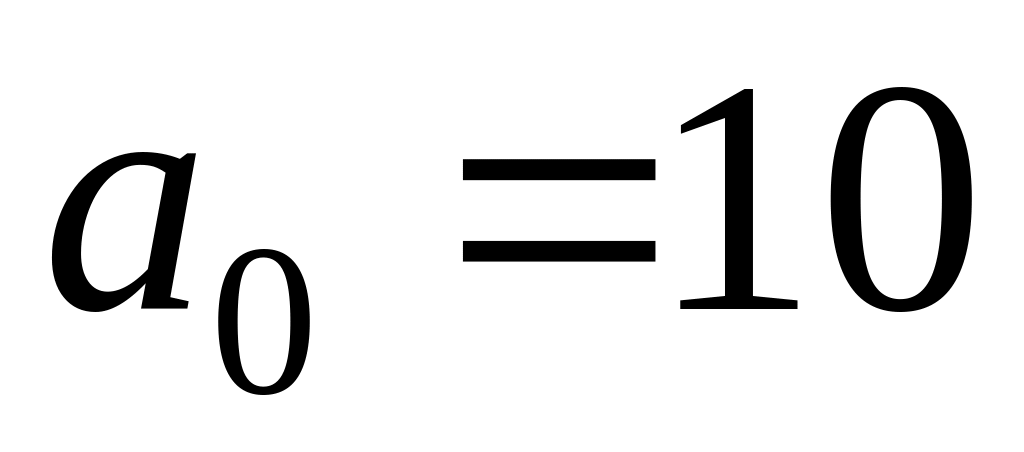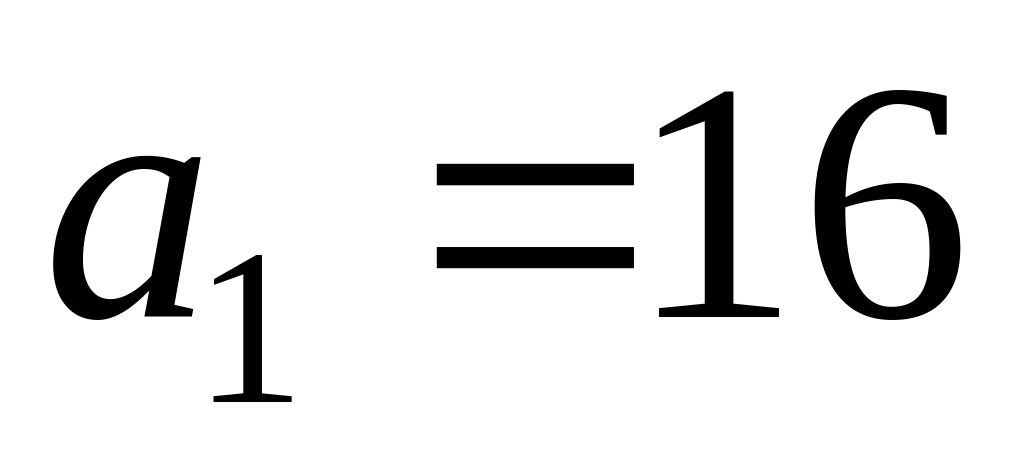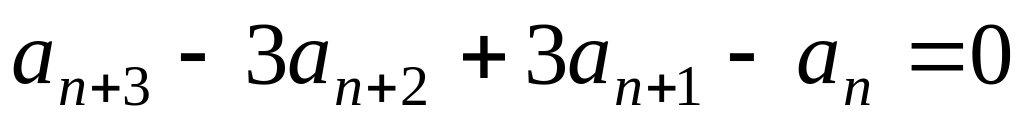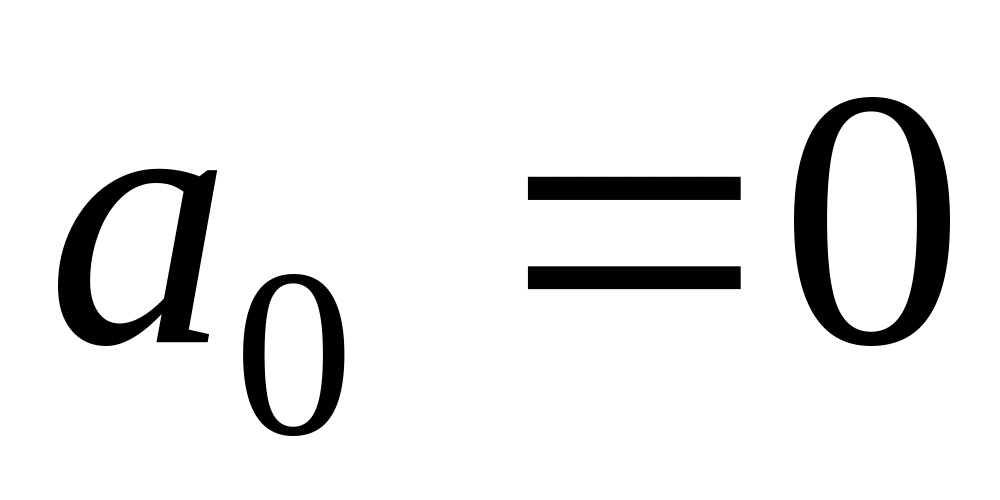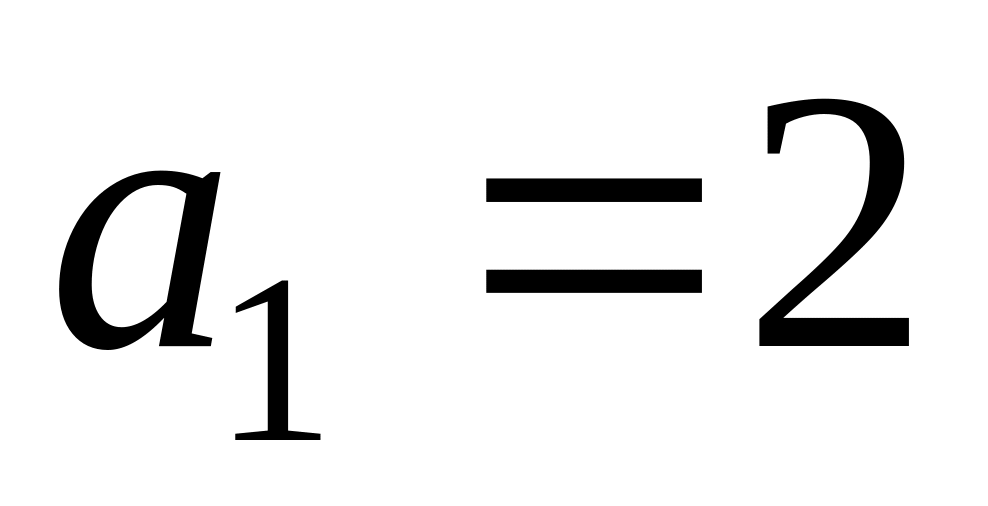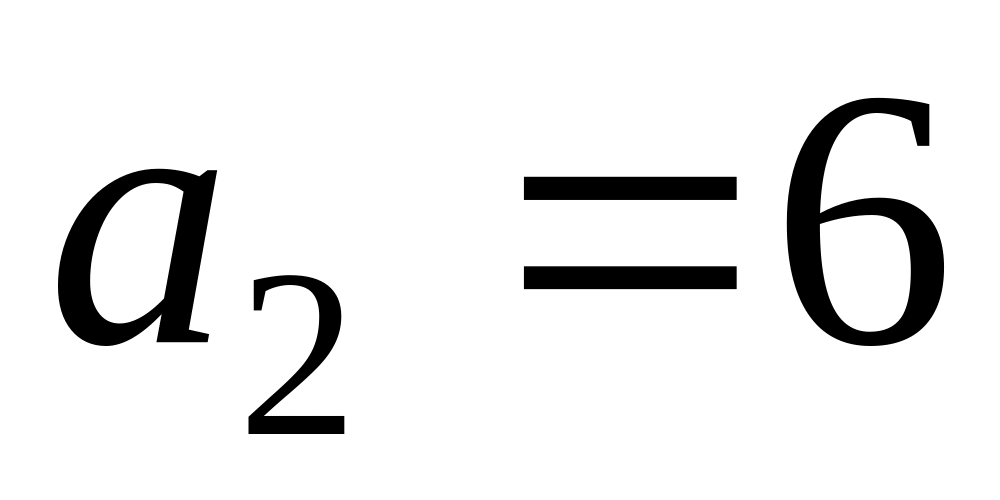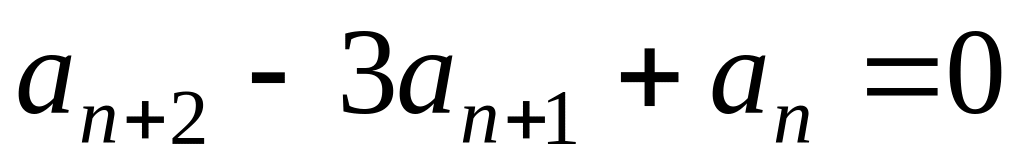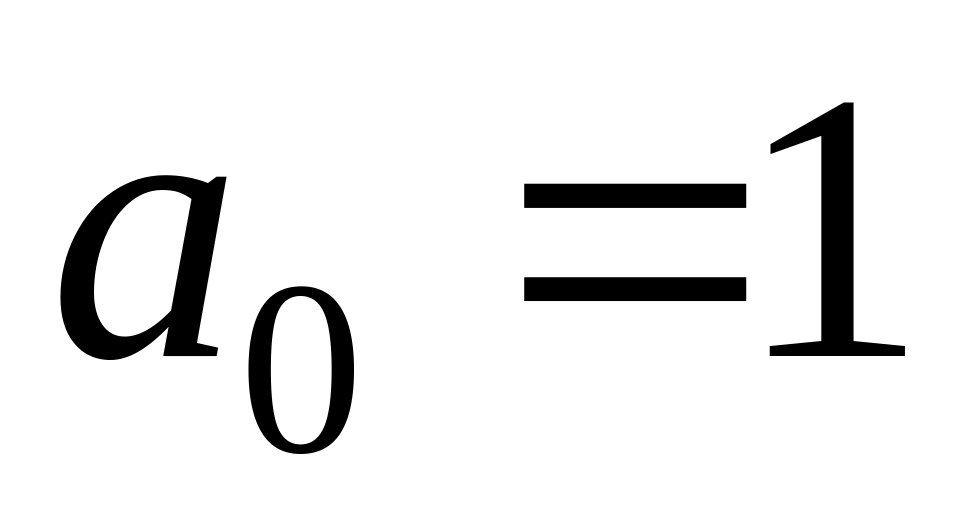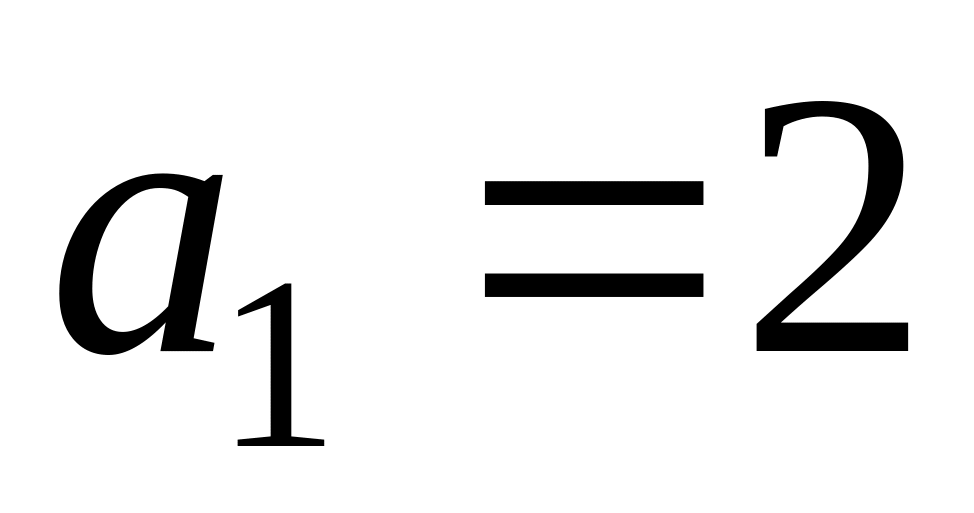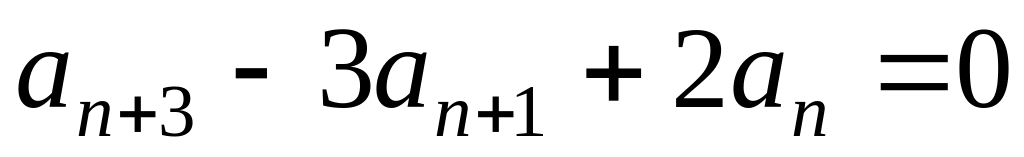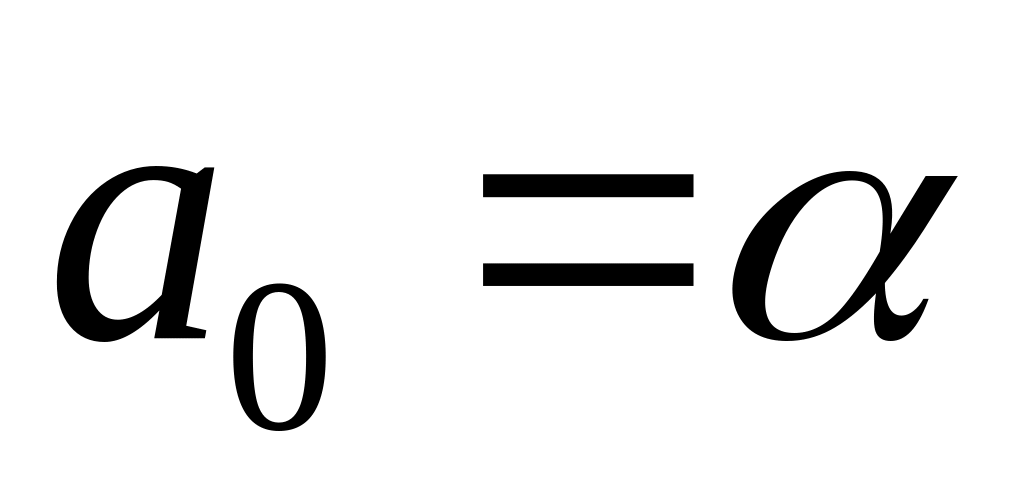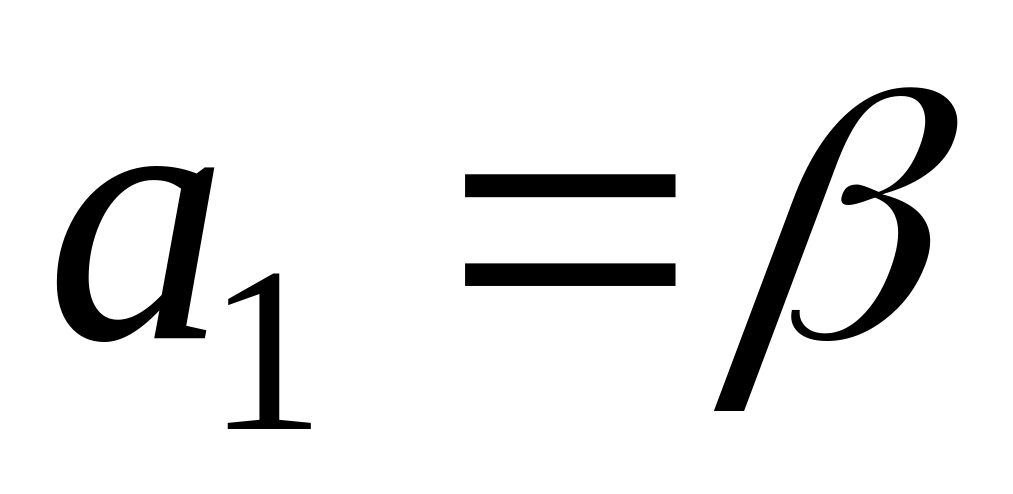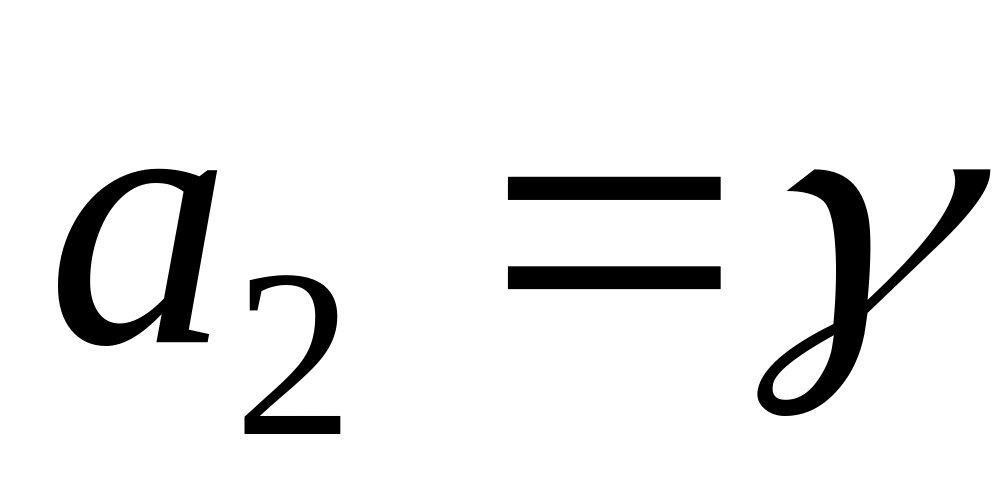Список літератури

1. В.А.Горбатов. Основы дискретной математики.— М.:Высшая школа, 1986. — 310 с.

2. Г.П.Гаврилов, А.А.Сапоженков. Сборник задач по дискретной математике. — М.:Наука, 1977. — 218 с.

3. Яблонский С.В. Введение в дискретную математику. – 2-е изд., перераб. и доп. — М.:Наука, 1986. — 384 с.

НАВЧАЛЬНЕ ВИДАННЯ

КОМБІНАТОРИКА