Методические указания к решению задачи 1

Решение этой задачи требует знания закона Ома для всей цепи и ее участков, первого закона Кирхгофа и методики определения эквивалентного сопротивления цепи при смешанном соединении резисторов.

ЗАДАЧА 1: для схемы, приведенной на рисунке 16а, определить эквивалентное сопротивление цепи R_АВ, токи в каждом резисторе и напряжение U_АВ, приложенное к цепи. Заданы сопротивления резисторов и ток I₄ в резисторе R₄. Как изменятся токи в резисторах при: а) замыкании рубильника Р1, б) расплавлении вставки предохранителя Пр4? В обоих случаях напряжение U_АВ остается неизменным.

Рисунок 16

Пример решения задачи 1

Задача относится к теме «Электрические цепи постоянного тока».

После усвоения условия задачи проводим поэтапное решение, предварительно обозначив стрелкой направление тока в каждом резисторе. Индекс тока должен соответствовать номеру резистора, по которому он проходит.

1. Определяем общее сопротивление разветвления R₂, R₃. Рассматриваемые резисторы соединены параллельно, поэтому сопротивление эквивалентного резистора R_2,3 определяется по формуле:

Теперь схема цепи принимает вид, показанный на рисунке 16б.

2. Резисторы R_2,3 и R₅ соединены последовательно, их общее сопротивление:

Соответствующая схема приведена на рисунке 16в.

3. Резисторы R_2,3,5 и R₄ соединены параллельно, их общее сопротивление R_2,3,4,5:

Теперь схема цепи принимает вид, показанный на рисунке 16г.

4. Находим эквивалентное сопротивление всей цепи:

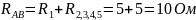(рисунок 16д)

5. Зная силу тока I₄, находим напряжение на резисторе R₄:

Это же напряжение приложено к резисторам R_2,3+R₅ (рисунок 16б). Поэтому ток в резисторе R₄

6. Находим падение напряжения на резисторе R₅:

Поэтому напряжение на резисторах R_2,3

7. Определяем токи в резисторах R₂ и R₃:

;

Применяя первый закон Кирхгофа, находим ток в резисторе R₁:

8. Вычисляем падение напряжения на резисторе R₁:

9. Находим напряжение U_АВ, приложенное ко всей цепи:

или

10. При включении рубильника Р1 сопротивление R₁ замыкается накоротко и схем цепи имеет вид, показанный на рисунке 16е. Эквивалентное сопротивление цепи в этом случае

.

Поскольку напряжение U_АВ остается равным 100 В, можно найти токи в резисторах R₄ и R₅ :

Определим падение напряжения на резисторе R₅

Поэтому напряжение на резисторах R₂ и R₃:

Теперь можно найти токи в резисторах R₂ и R₃:

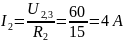
=6 A

Проверим правильность вычисления токов, используя первый закон Кирхгофа:

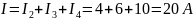
Однако

Таким образом, задача решена верно.

11. При расплавлении предохранителя Пр4 резистор R₄ выключается и схема принимает вид, показанный на рисунке 16ж.

Вычисляем эквивалентное сопротивление схемы:

Поскольку напряжение U_АВ остается неизменным, находим токи I₁ и I₅:

Напряжение на резисторах R₂, R₃

Находим токи I₂, I₃

Сумма этих токов равна току I₁:

Методические указания к решению задачи 2

Эта задача относится к неразветвленным цепям переменного тока.

Перед ее решением изучите матерал темы 1.4, ознакомьтесь с методикой построения векторных диаграмм и рассмотрите решение типового примера.

Задача 2. Активное сопротивление катушки R_к=6 Ом, инуктивное X_L=10 Ом. Последовательно с катушкой включено активное сопротивление R=2 Ом и конденсатор сопротивлением X_C=4 Oм (рисунок 17,а). К цепи прилодено напряжние =50 В (действующее значение). Определить: 1)полное сопротивление цепи; 2)ток; 3)коэффициент мощности; 4)активную, реактивную и полную мощности; 5)напряжения на каждом сопротивлении. Начертите в масштабе векторную диаграмму цепи.

РЕШЕНИЕ 1. Определяем полное сопротивление цепи:

=10 Ом.

2. Определяем ток:

3. Определяем коэффициент мощности цепи:

По таблицам Брадиса находим φ=36⁰50’. Угол сдвига фаз φ находим по синусу во избежание потери знака угла (косинус является четной функцией).

Рисунок 17

4. Определяем активную мощность цепи:

или

Вт

Здесь

5. Определяем реактивную мощность цепи:

или

вар

6. Определяем полную мощность цепи.

В

или

7. Определяем падения напряжения на сопротивлениях цепи:

B; 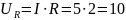B; B; .

Построение векторной диаграммы начинаем с выбора масштаба для тока и напряжения. Задаемся масштабом по току: в 1 см – 1,0А и масштабом по напряжению: в 1 см – 10 В. Построение векторной диаграммы начинаем с вектора тока, который откладываем по горизонтали в масштабе .

Вдоль вектора тока откладываем векторы падений напряжения на активных сопротивлениях U_Rк и U_R:

; .

Из конца вектора U_R откладываем в сторону опережения вектора тока на 90 вектор падения напряжения U_L на индуктивном сопротивлении длиной . Из конца вектора U_L откладываем в сторону отставания от вектора тока на 90 вектор падения напряжения на конденсаторе U_С длиной . Геометрическая сумма векторов U_Rк, U_R, U_L и U_С равна полному напряжению U, приложенному к цепи.