3. Построение овала

Построение овала по двум осям (рисунок 3) осуществляется в следующей последовательности:

– проводим осевые линии, на которых симметрично от точки O пересечения (рисунок 3а) откладываем отрезки AB и CD, равные большой и малой осям овала;

– откладываем на малой оси расстояние OE=OA и соединяем точки A и C;

– откладываем на отрезке AC отрезок CF=CE;

– делим отрезок AF пополам;

– проводим через точку K прямую перпендикулярную AF до пересечения с большой и малой осями овала в точках O₁ и O₂;

– строим зеркальное отображение точек O₁ и O₂ (точки O₃ и O₄) и прямой О₂К;

– проводим из точки О₄ прямые линии через точки О₁ и О₃ (рисунок 3а);

– проводим из точек O₂ и O₄ радиусом R= O₂C, а из точек O₁ и O₃ радиусом R₁=O₁A дуги до их пересечения с прямыми, проведенными через центры дуг (рисунок 3б).

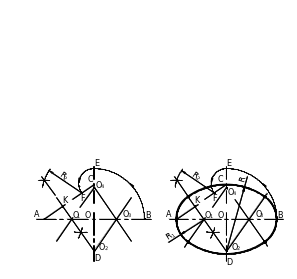
а) б)

Рисунок 3

4. Построение эллипса

Построение эллипса по двум осям выполняется в следующей последовательности (рисунок 4):

– проводим осевые линии, на которых симметрично от точки O пересечения откладываем отрезки AB и CD, равные большой и малой осям эллипса;

– строим две окружности радиусами равными половине осей эллипса с центром в точке пересечения осей;

– делим окружность на двенадцать частей;

– проводим через полученные точки лучи-диаметры (рисунок 4а);

– проводим из точек пересечения лучей с соответствующими окружностями прямые линии параллельно осям эллипса до их взаимного пересечения;

– соединяем полученные точки плавной кривой линией при помощи лекал (рисунок 4б). При построении лекальной кривой линии необходимо выбирать и располагать лекало так, чтобы соединялось как минимум четыре-пять точек.

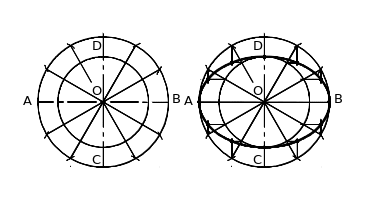
а) б)

Рисунок 4

5. Построение параболы

Последовательность вычерчивания параболы такова (рисунок 5):

– проводим горизонтальную прямую линию, на которой отмечаем вершину O и откладываем длину оси OK=a мм (рисунок 5а);

– проводим через точку K перпендикуляр, на котором симметрично вверх и вниз откладываем длину хорды параболы DC=b мм;

– строим прямоугольник ABCD, в котором одна сторона равна оси, а другая – хорде параболы;

– делим на несколько равных частей сторону BC и настолько же равных частей отрезок KC;

– проводим из вершины параболы O лучи через точки 1, 2…С, а через точки 1₁, 2₁…С проводим прямые параллельные оси (рисунок 5а);

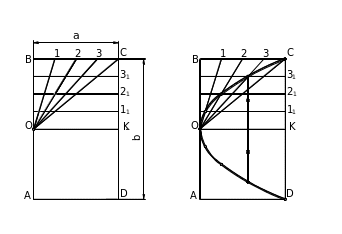
а) б)

Рисунок 5

– определяем точки, принадлежащие параболе. Например, при пересечении луча О2 с параллельной прямой 2₁ получаем точку, принадлежащую параболе;

– полученные точки соединяют плавной кривой линией с помощью лекала. Вторая ветвь параболы строится аналогично (рисунок 5б).

6. Построение гиперболы

Построение выполняется следующим образом (рисунок 6):

– проводим горизонтальную прямую линию, на которой откладываем расстояние с между вершинами – точки A и B;

– откладываем от точки А расстояние равное длине хорды a (точка О), от которой вверх и вниз симметрично откладываем длину хорды b (отрезки ОC и ОD);

– строим прямоугольник KNDC. Сторону прямоугольника KC делим на пять равных частей, а сторону ОC на такое же число равных частей;

– соединяем вершину A с точками 1, 2, …, C, а вершину B с точками 1₁, 2₁,…, C (рисунок 6а).

– определяем точки пересечения луча А1 с лучом В1₁, луча А2 с лучом В2₁ и т. д.

– соединяем полученные точки пересечения плавной кривой линией под лекало.

Остальные ветви гиперболы строим как зеркальное отображение построенной ветви (рисунок 6б).

а) б)

Рисунок 6