Лабораторная работа № 8.

Производная.

Опр.1. Производной функции по аргументу называется предел отношения приращения функции в точке к приращению аргумента при условии, что это последнее стремиться к нулю. Производная функции обозначается .

Таким образом, по определению

Операция отыскания производной данной функции называется дифференцированием этой функции.

Геометрически число представляет собой угловой коэффициент касательной к графику функции в точке .

Пример 1. Исходя из определения производной, непосредственно найти производную функции у=х².

Решение:

Придадим х приращение х и найдем приращение функции:

у=у(х+х)-у(х)=(х+х)²-х²=х²+2хх+(х)²-х²=2хх+(х)²

Основные правила нахождения производной.

Если с - постоянная величина и функции u=u(x), v=v(x), w=w(x)

имеют производные, то

1. (с)^/=0

2. (cu)^/=cu^/

3. (u+v-w)^/=u^/+v^/+w^/

4. (uv)^/=u^/v+uv^/

5)

6)

7) если функции и имеют производные, то y_x^/ =y_u^/ u_x^/ .

Пример 2.Вычислить производную функции: y=(2x² –5x+1)e^x

Решение:

y^/ =(2x² –5x+1)^/ e^x +(2x² –5x+1)(e^x )^/ =(по правилу 4)=[(2x² )^/ –(5x)^/ +1^/]e^x +(2x² –5x+1)e^x =

=(по правилу 3)=(4x-5)e^x +(2x² –5x+1)e^x .

Если х- независимая переменная, то

Основные формулы.

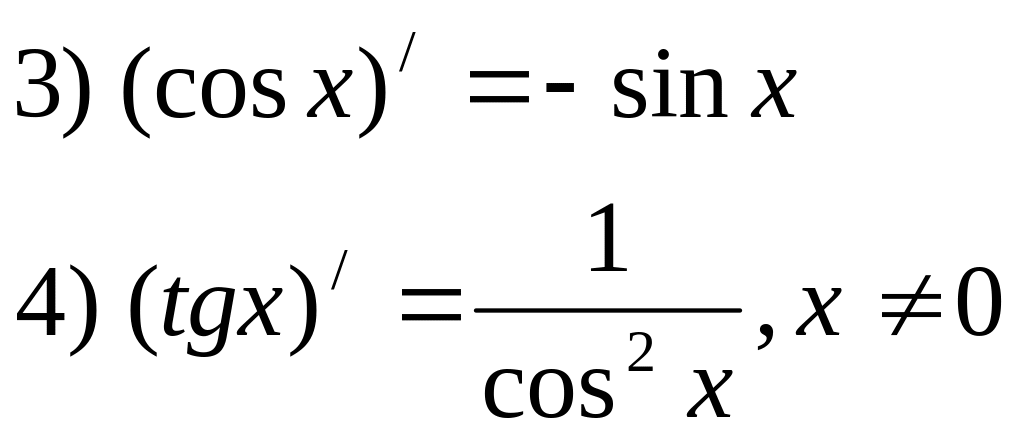
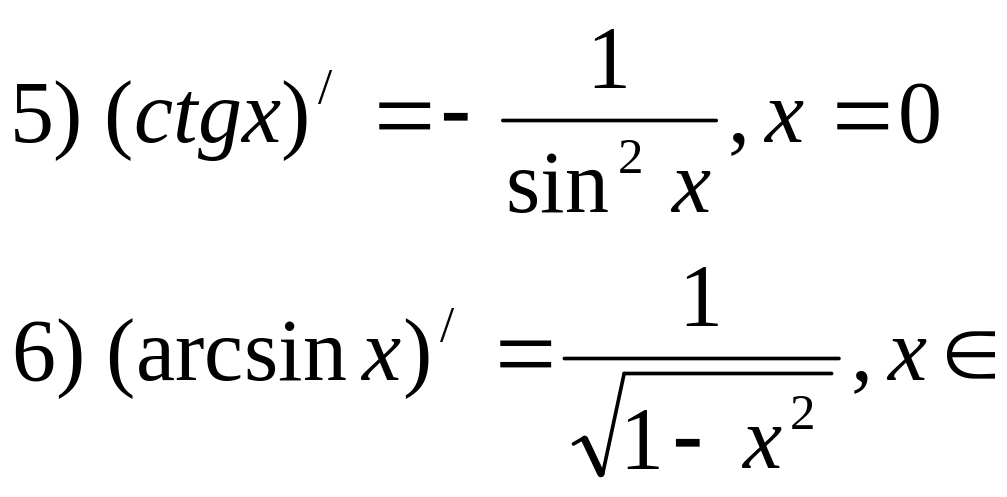
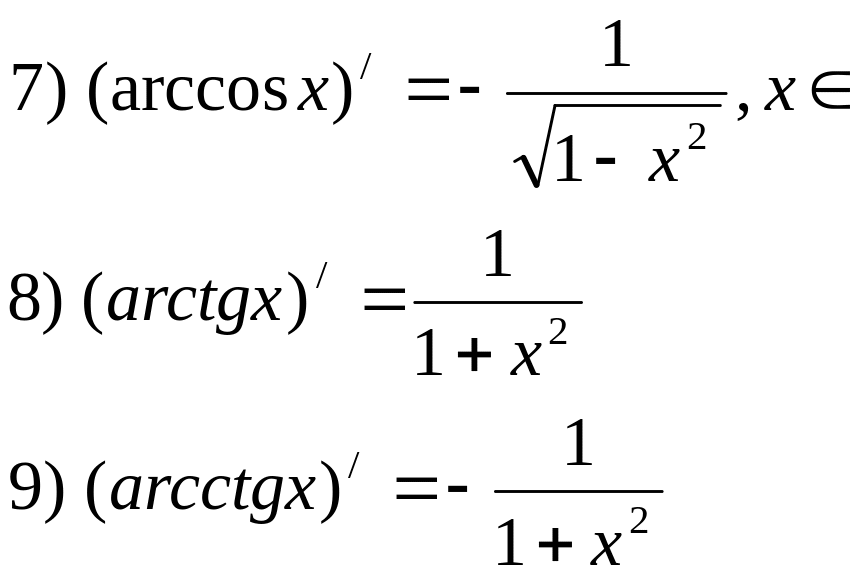
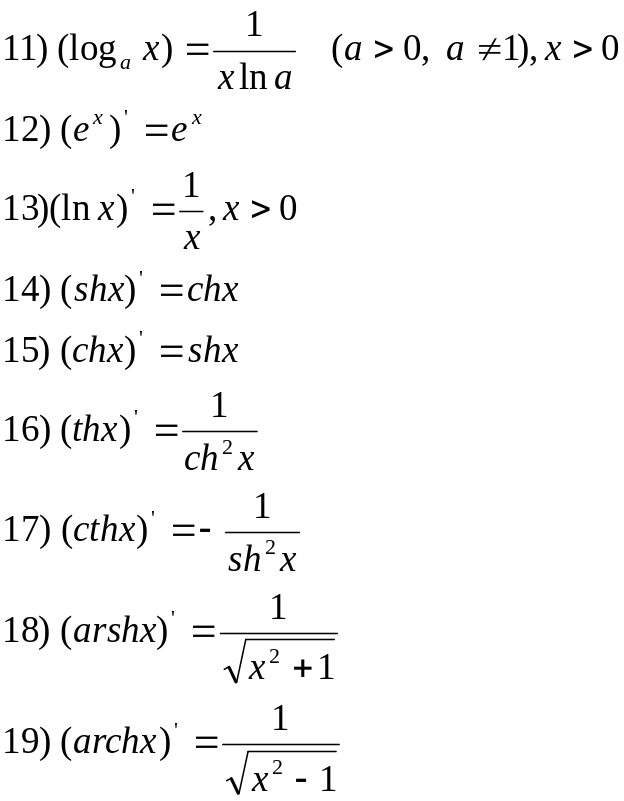
Пример 3. Вычислить производную функции:

Решение:

Воспользуемся сначала правилом 5), а затем правилами 3) и 4) и формулами 2) и 3).

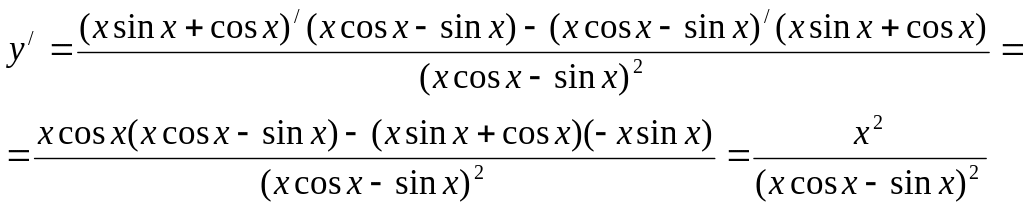
ВАРИАНТЫ.

1. Исходя из определения производной, непосредственно найти производные функций:

2. Пользуясь основными правилами нахождения производных и таблицей производных, вычислить производные функций:

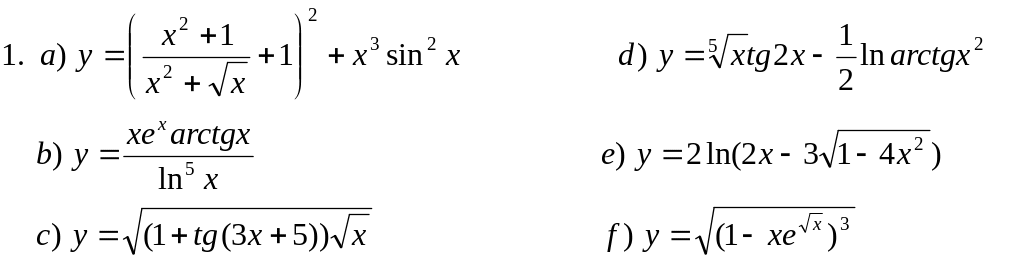
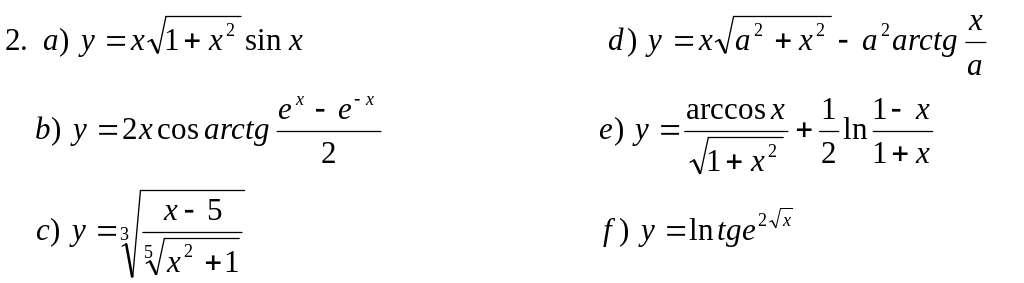
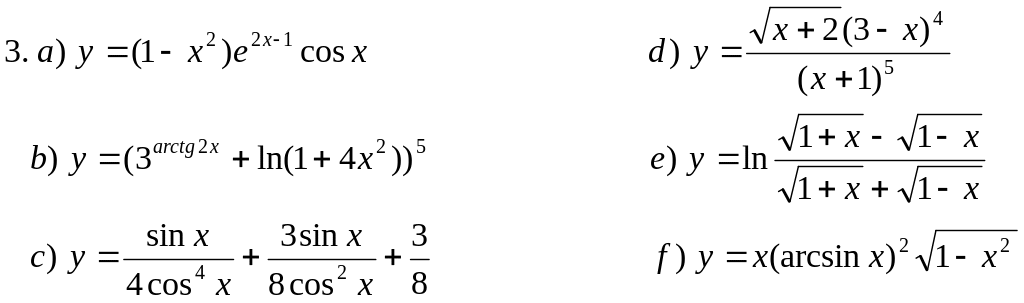
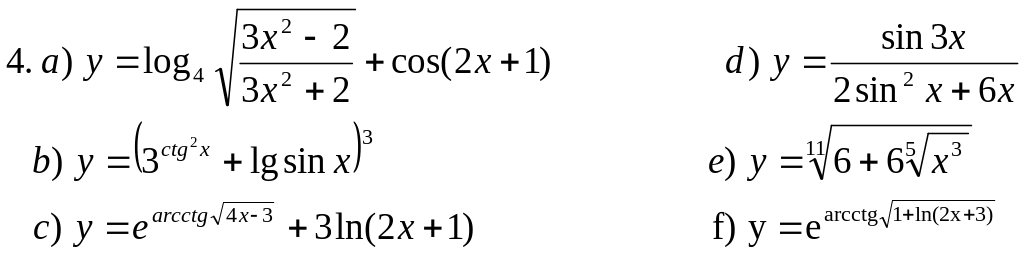
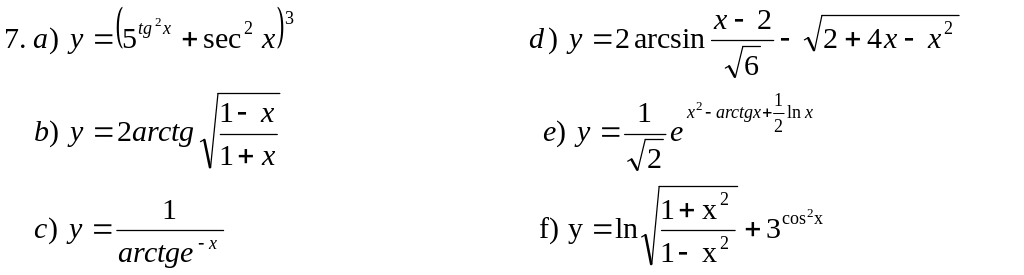
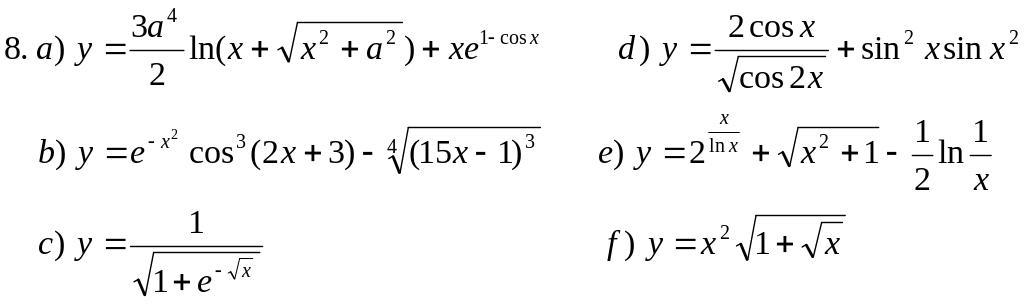
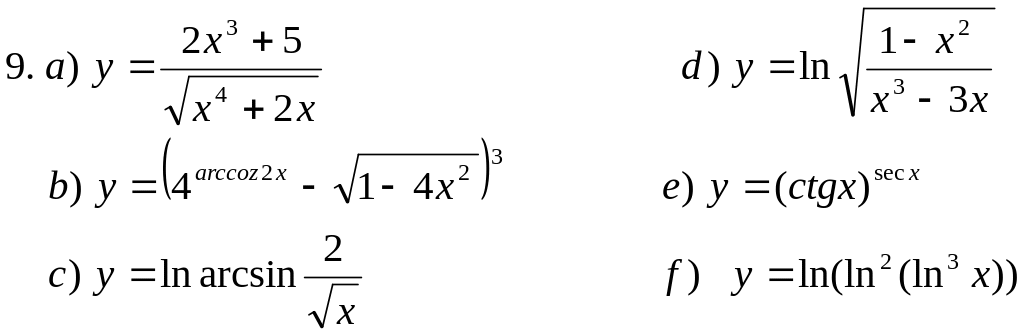
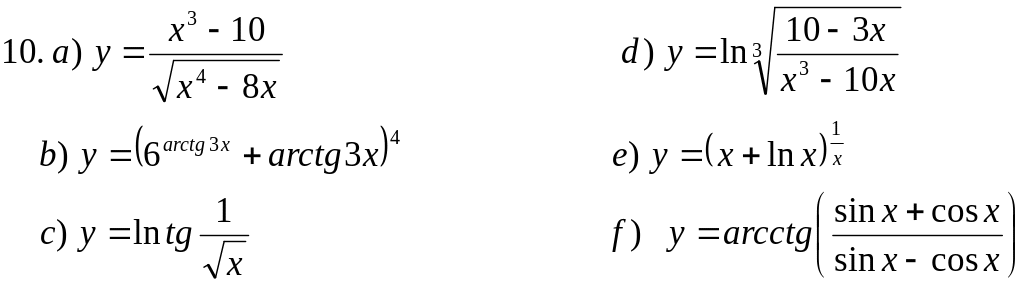
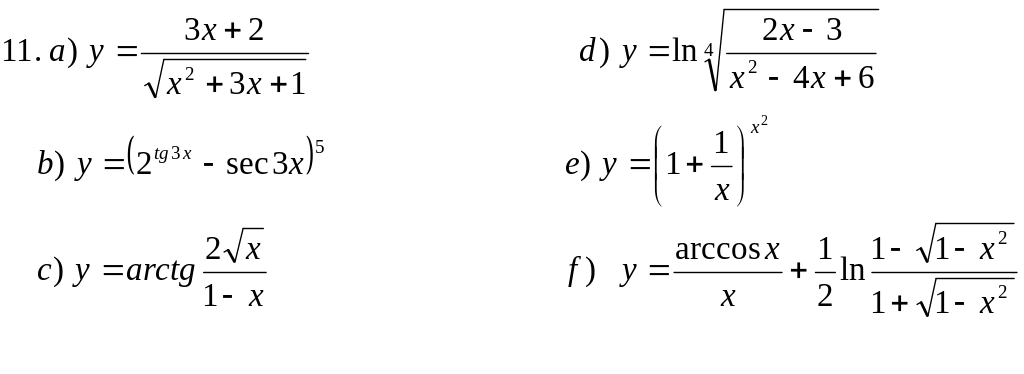
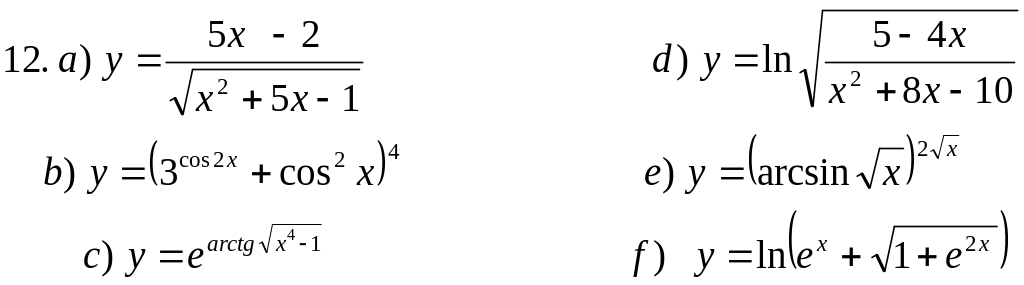
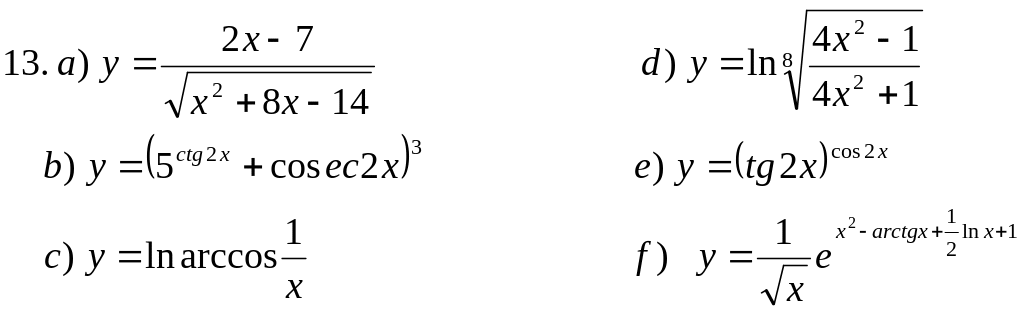
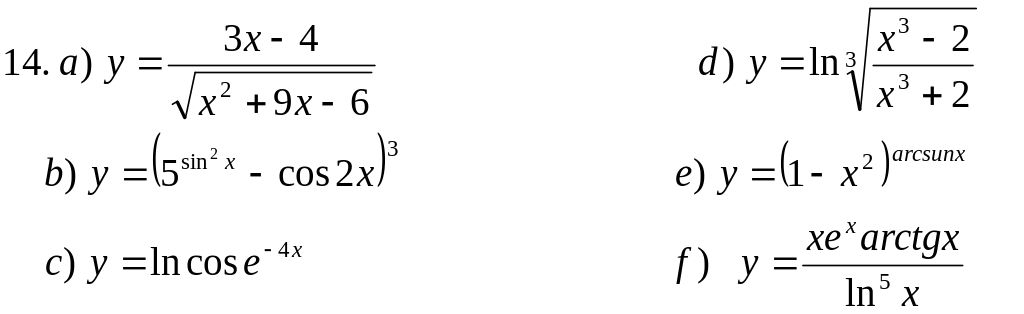
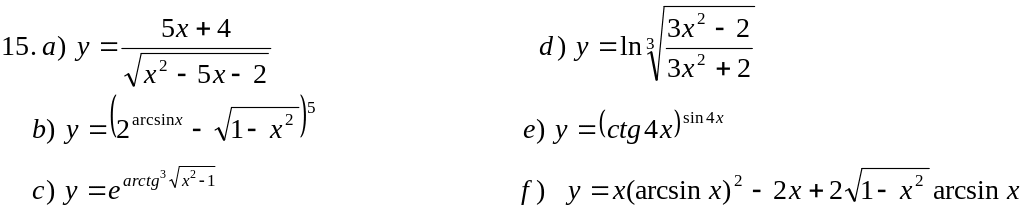
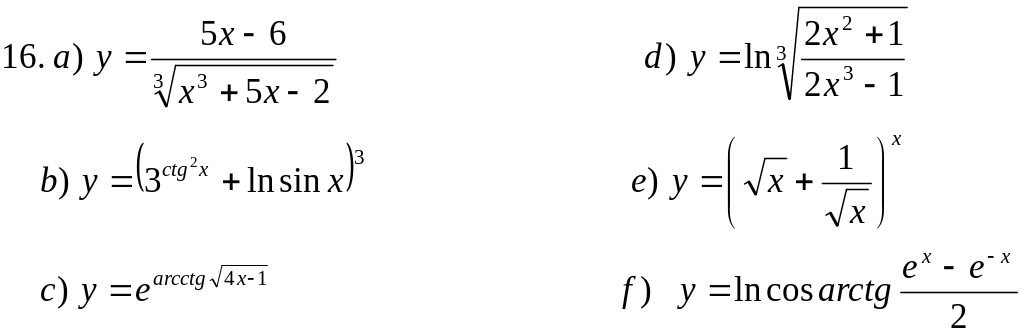
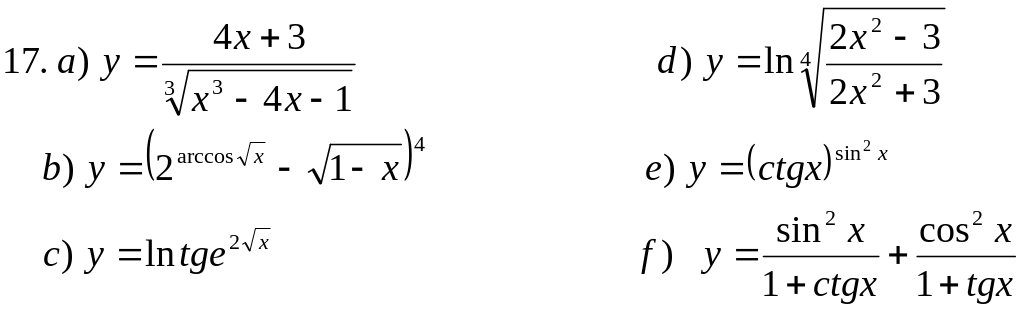
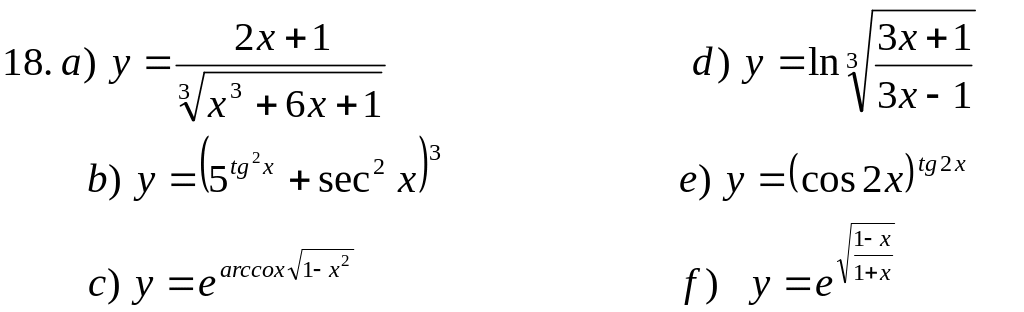
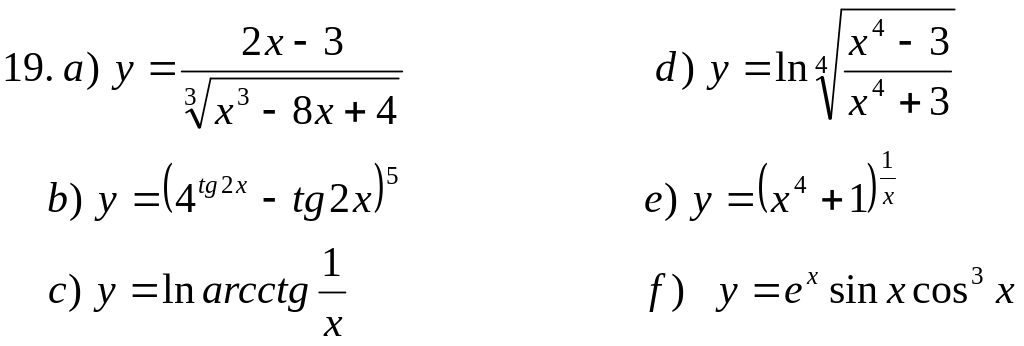
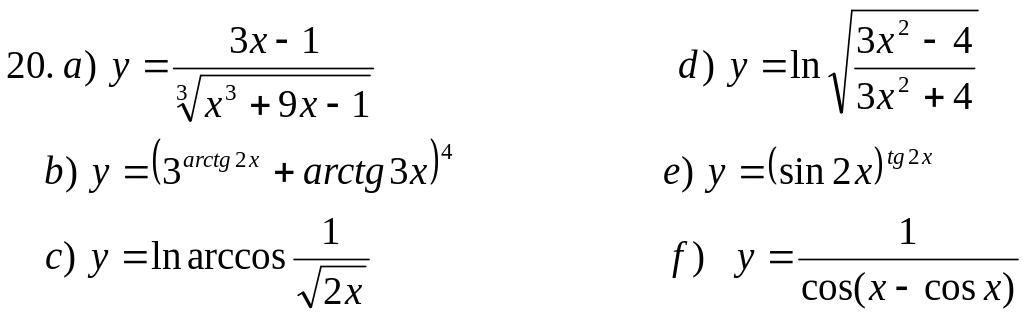
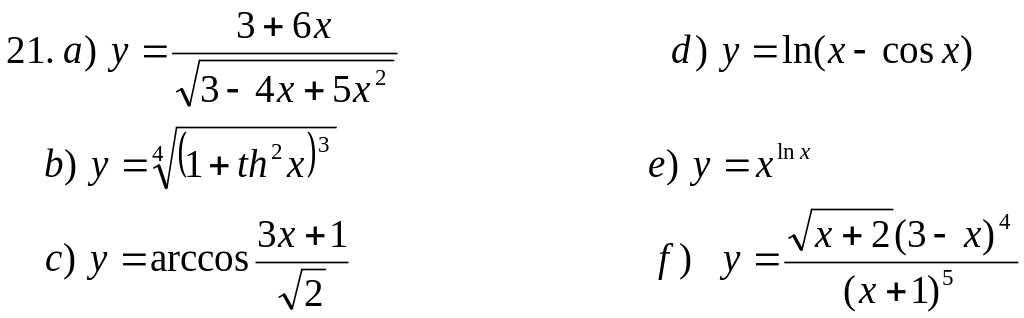
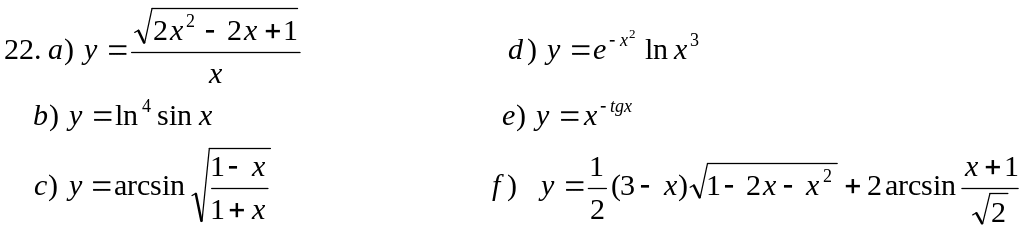
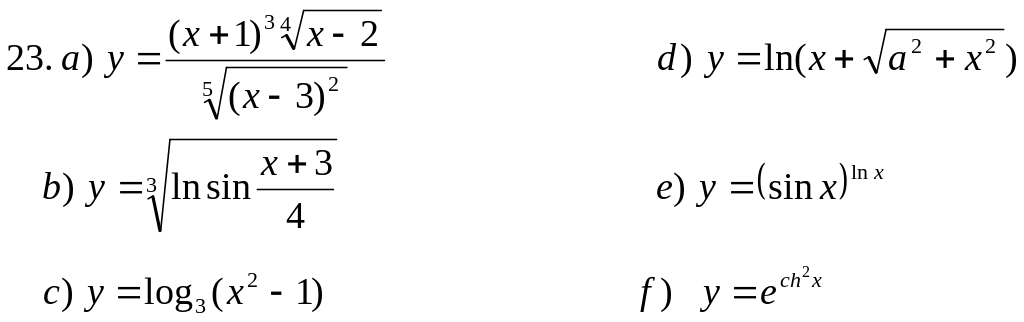
Лабораторная работа № 9. Дифференциал и дифференцируемость функции.

Опр.1. Функция y=f(x): v(x₀)R называется дифференцируемой в точке х₀ , если ее приращение в этой точке y=f(x₀+x)-f(x₀).

x=x-x₀, представимо в виде:

y=A x+(x)x, (1)

где А- некоторая const, не зависящая от x , а (х)0 при х0.

Опр.2. Главная линейная часть приращения функции относительно х называется дифференциалом функции f в точке х₀ и обозначается df(x₀) или, короче, dy=Ax. Таким образом,

y=dy+0(x) при х0 (2).

Т.к.

Для большей симметрии записи дифференциала приращение х обозначают dх и и называют его дифференциалом независимого переменного. Таким образом, dy=Adx.

Пример 1. Доказать, что функция y=x²-x+3 диффенцируема

на R.

Решение: возьмем хR, дадим ей приращение х, тогда

у=f(x+x)-f(x)=(x+x)²-(x+x)+3-(x²-x+3)=x²+2xx+(x)²-x-x+3-x²+x-3= (2x-1)x+(x)²

где (х)²=0(х), т.к. =х0 при х0.

Т.о. у=Ах+0(х), где А=2х-1, т.е. у представимо в виде (1) в хR.

Теорема: Для того, чтобы функция y=f(x):U(x₀)R была дифференцируемой в точке х₀ она имела производную в х₀, при этом dy=f ^/(x₀)dx.

Пример 2. Доказать, что функция не дифференцируема в точке =0.

Решение: Имеем

т.е. в точке =0 не дифференцируема.

Пример 3. Пользуясь понятием дифференциала, найти приближенное значение

Решение: рассмотрим функцию ,тогда

- есть значение данной функции при х=0,15

Пусть х₀=0, х=0,15. Тогда у(0)=1.

Из (2) видно, что y=dy, a dy=f ^/x ,т.е.

yf ^/(x)x, y=f(x+x)-f(x) .

Отсюда f(x+x)f(x)+f ^/(x)x . В нашем. случае x=0,

x+x=0,15; f(0,15)f(0)+f ^/(0) 0,15.

Определим

В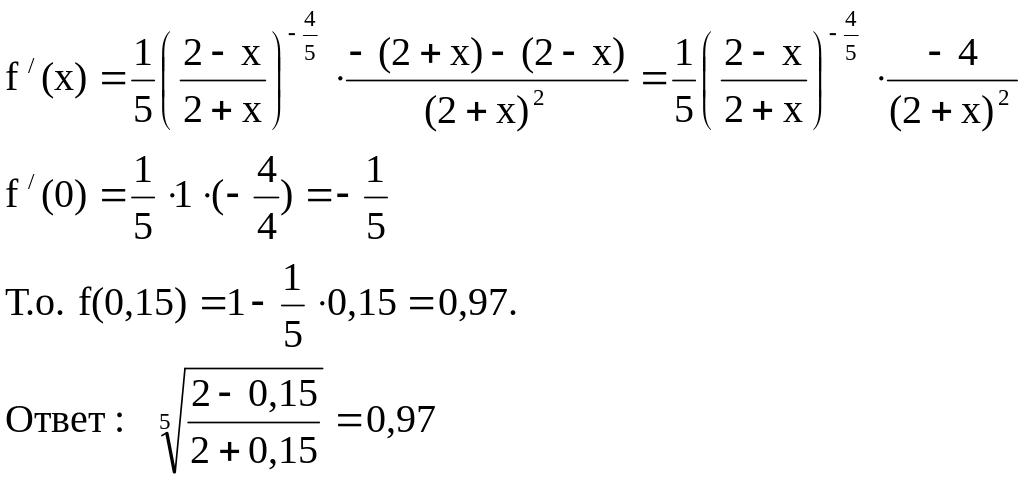 АРИАНТЫ.

1. Доказать, что функция f(x) не дифференцируема в точке х.

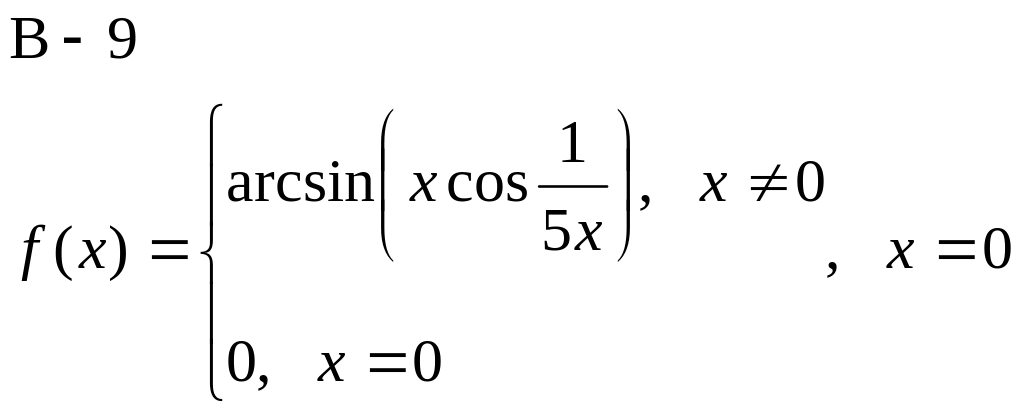
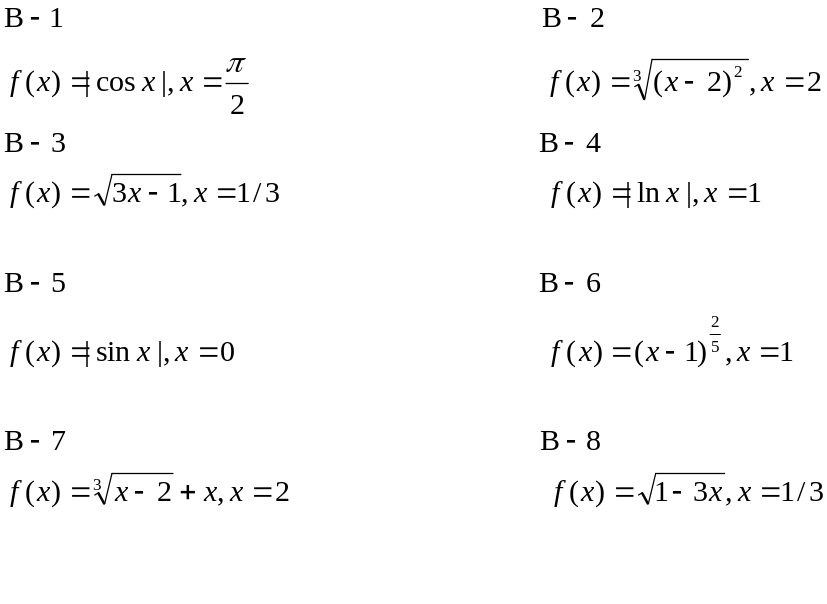
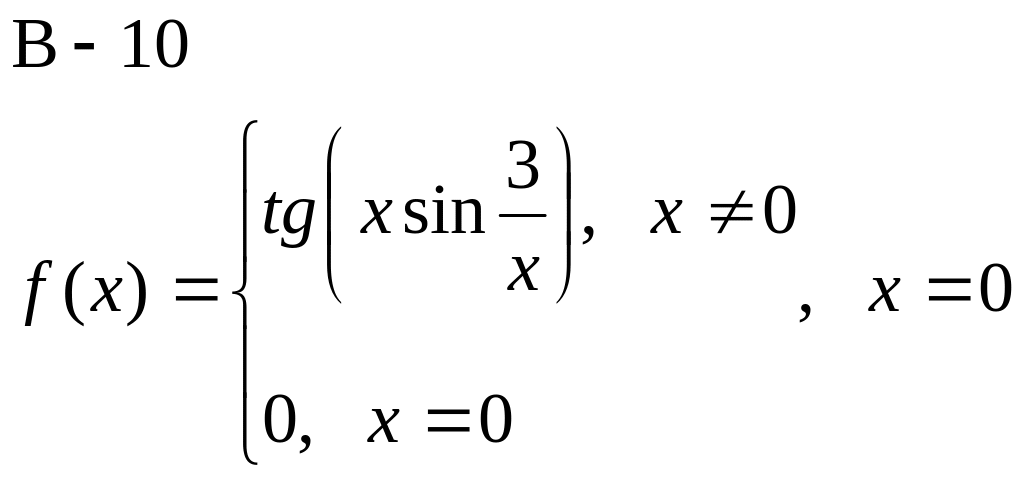
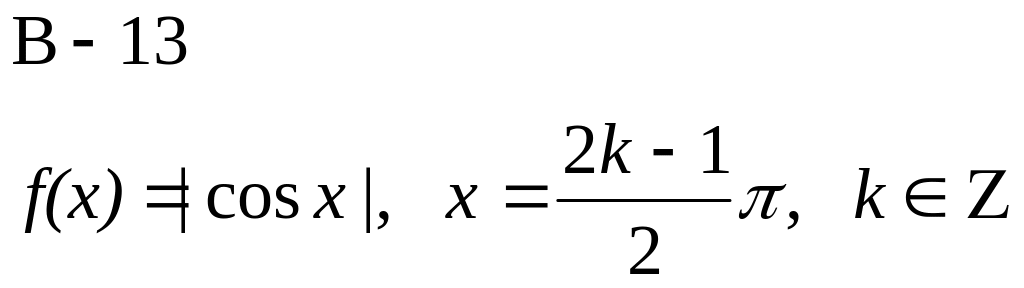
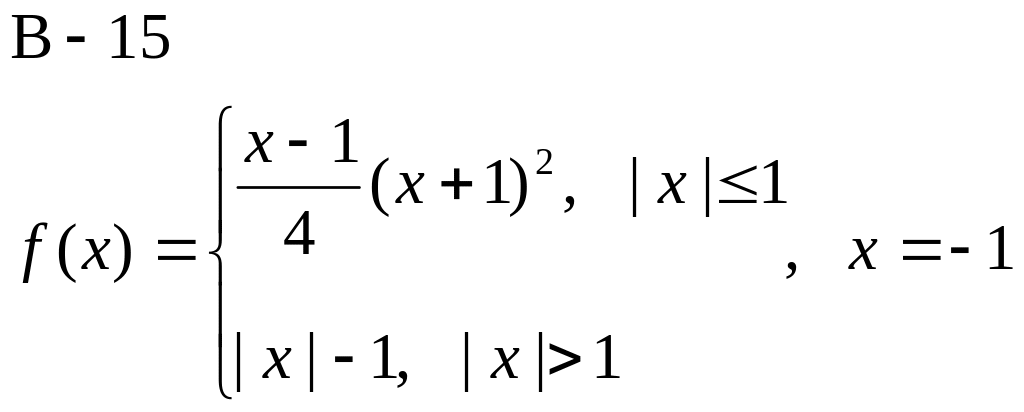
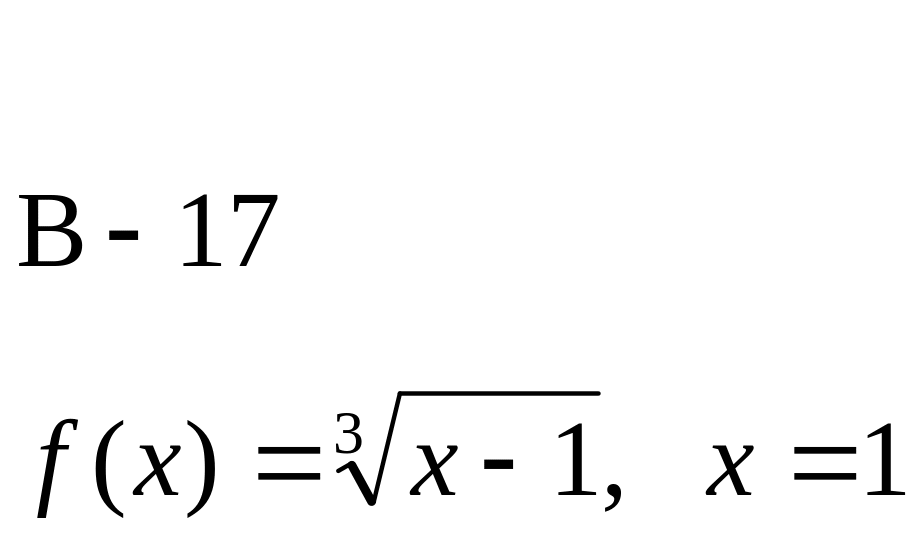
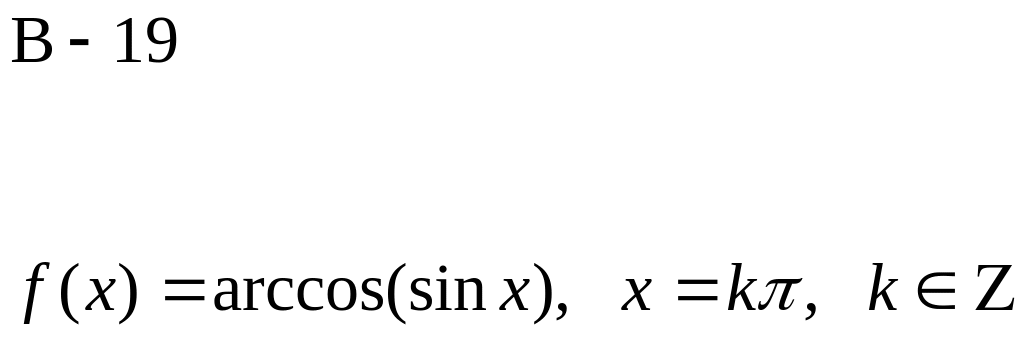
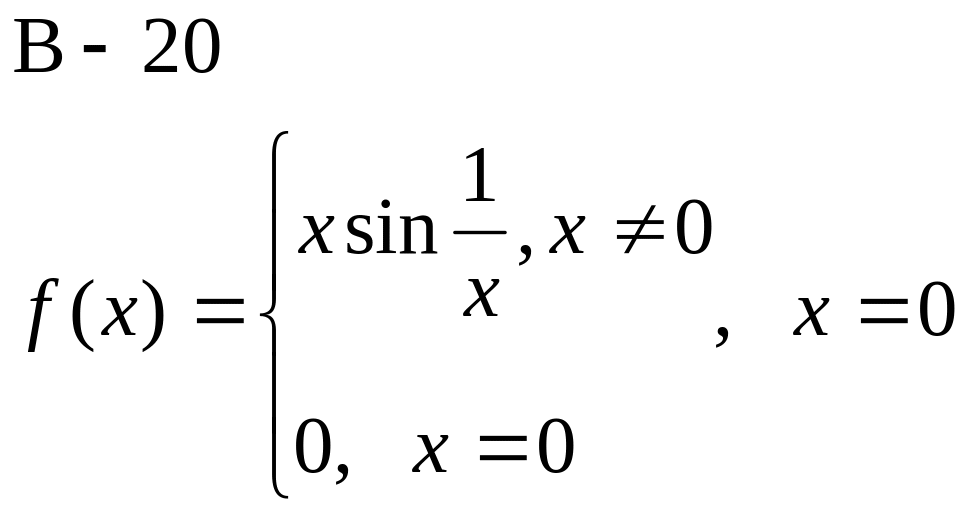
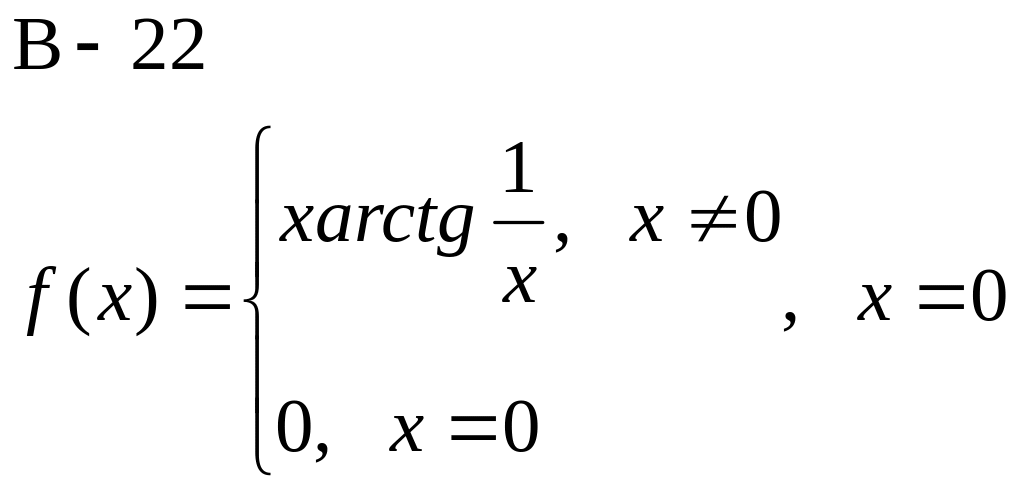
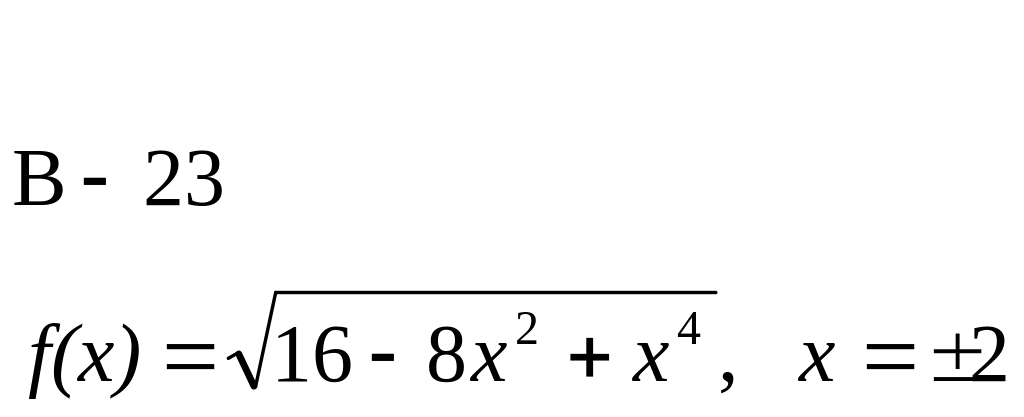
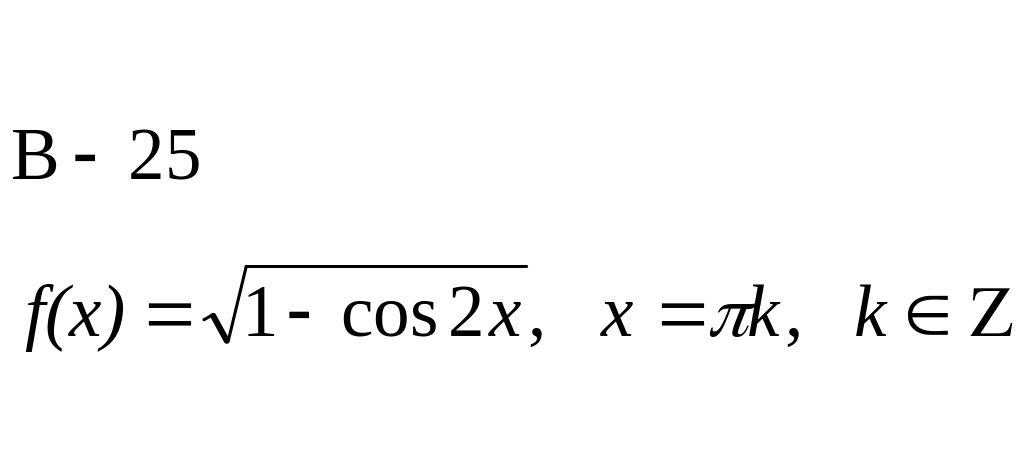
2. Найти дифференциалы функций:

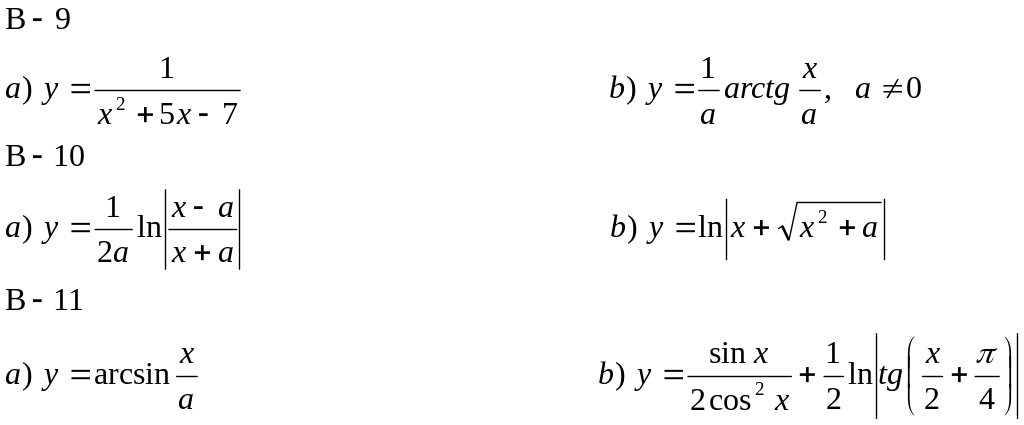
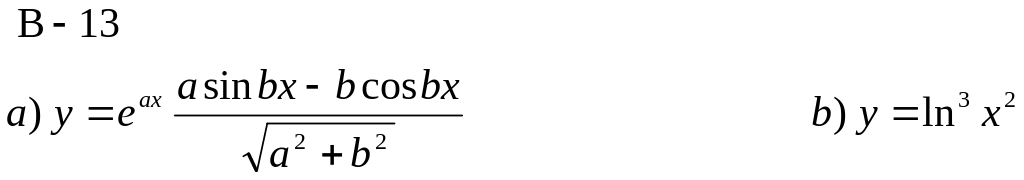
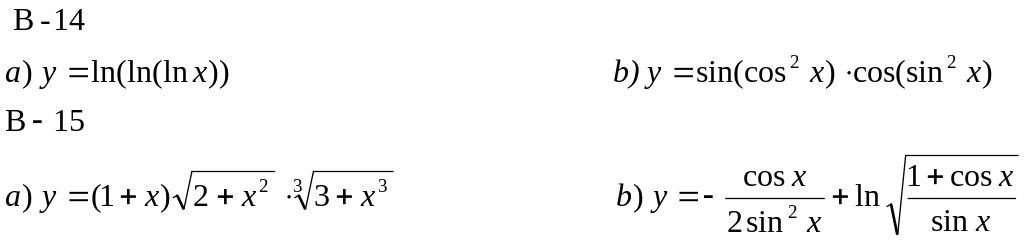
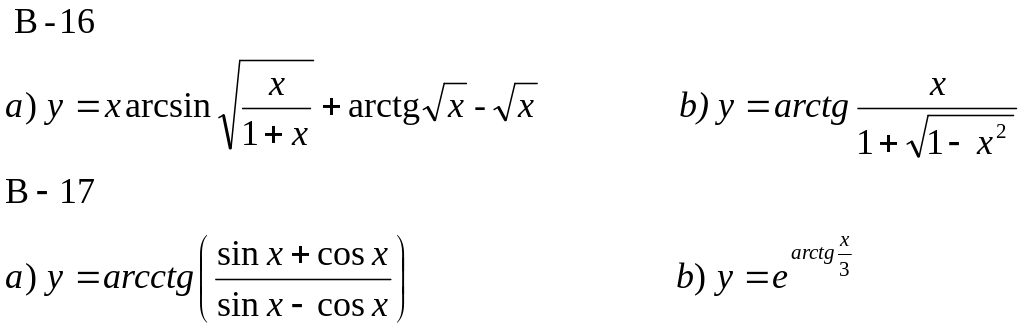
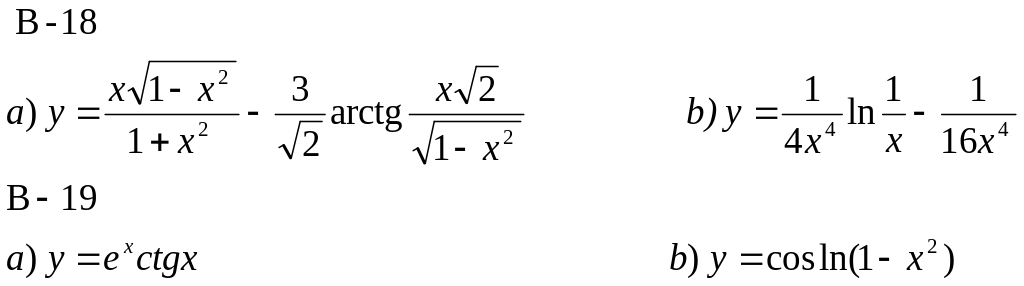
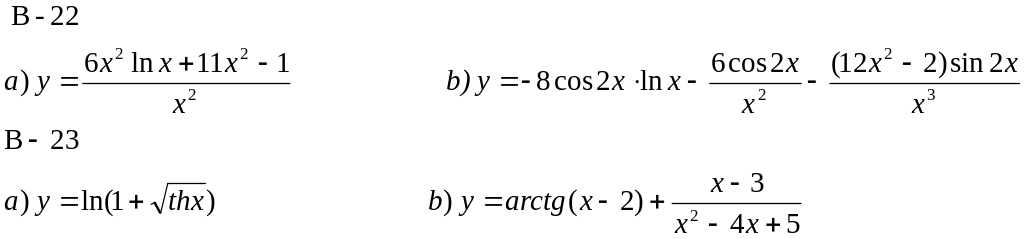
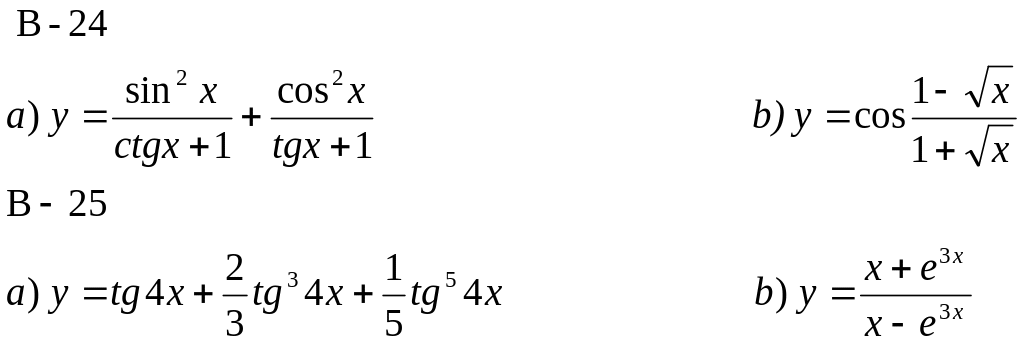
3. Найти приближенное значение функции:

В-1 B-2

y=x⁵-2x⁴+3x³-4x²+6, x=1,001 y=(x-3)²(x-2)³(x-4), x=4,001

B-3 B-4

y=ctgx, x=45⁰10^/ y=xln(x-2), x=3,001

B-5 B-6

(33)^1/5 lg 10,21

B-7 B-8

arctg 1,05 cos 31⁰

В-9 B-10

cos63⁰ tg46⁰

B-11 B-12

sin32⁰ ctg43⁰

B-13 B-14

sin27⁰ cos59⁰

B-15 B-16

tg43⁰ sin29⁰

B-17 B-18

cos62⁰ tg43⁰

B-19 B-20

sin33⁰ cos57⁰

B-21 B-22

ctg47⁰

B-23 B-24

B-25