Решение: возьмем

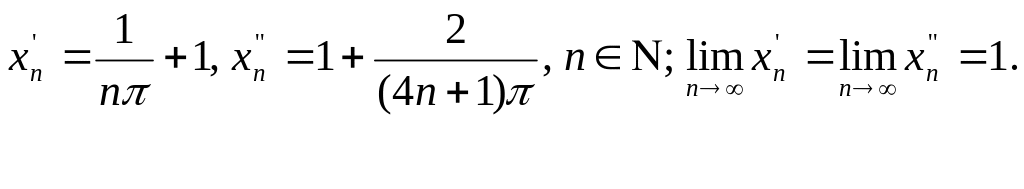
Тогда соответствующие последовательности значений функции таковы:

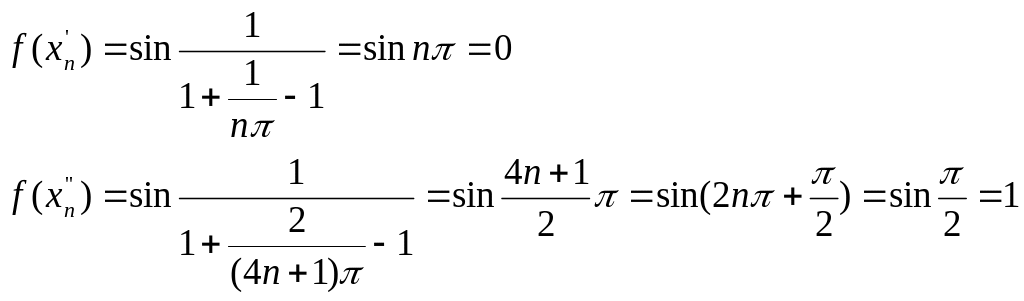
Следовательно,

, т.е. не существует

Замечание 2: Пример 2 показывает, что вывод о наличии предела функции нельзя делать, исходя из последовательности {x_n} частного вида (например, исходя из x_n^'' =1+ ), а нужно рассматривать произвольную последовательность {x_n }, имеющую заданный

предел а.

Пример 3: Пользуясь " – " определением предела, доказать, что

Р ешение: Надо доказать, что для >0 существует такое _ >0, что из неравенства 0 < |x-1| < _ следует, что |f(x)-1| < , f(x)=4x-3. Зададим

 > 0 и рассмотрим выражение: |f (x)-1|=|4x-3-1|= 4|x-1|.

Если взять _ ≤ /4, то для всех х, удовлетворяющих неравенству |x-1| < _, будем иметь |f(x)-1| = 4|x-1|<4_ ≤ 4/4=.

Следовательно,

Пример 4: f(x)=1/(x-1) доказать, что

Решение: По определению , если для  М>0 можно подобрать _М>0, что для всех ха, удовлетворяющих неравенству

0<|x-a|<, будет выполняться условие >M. В нашем случае по заданному M>0 будем подбирать _М из условия

| 1/|x-1|>M  |x-1|<1/M.

Следовательно, положив _M=1/М, получим, что для всех х, удовлетворяющих неравенству 0<|x-1|<_M, выполняется неравенство M, значит,

ВАРИАНТЫ.

1. Доказать, что предел функции не существует:

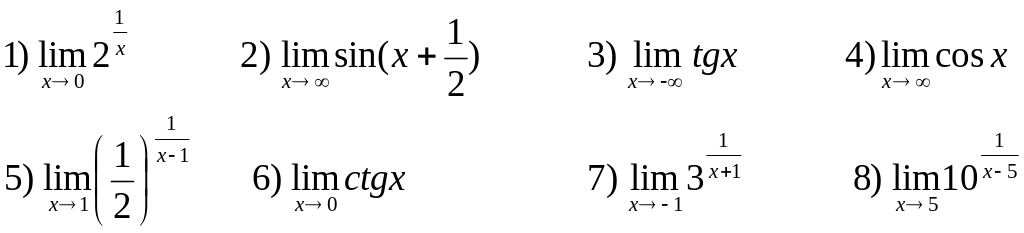
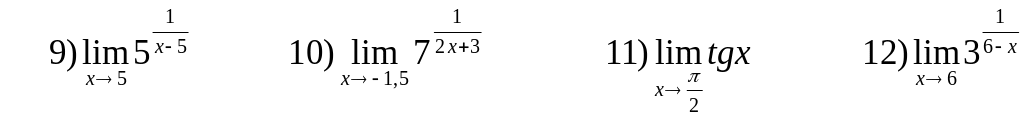
2. Доказать с помощью "-" определения существования следующих пределов и по заданным , подобрать _: ₁=0,5;₂=1;₃=1/100.

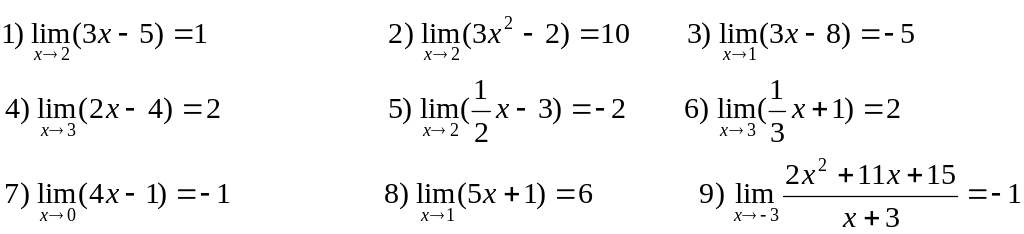
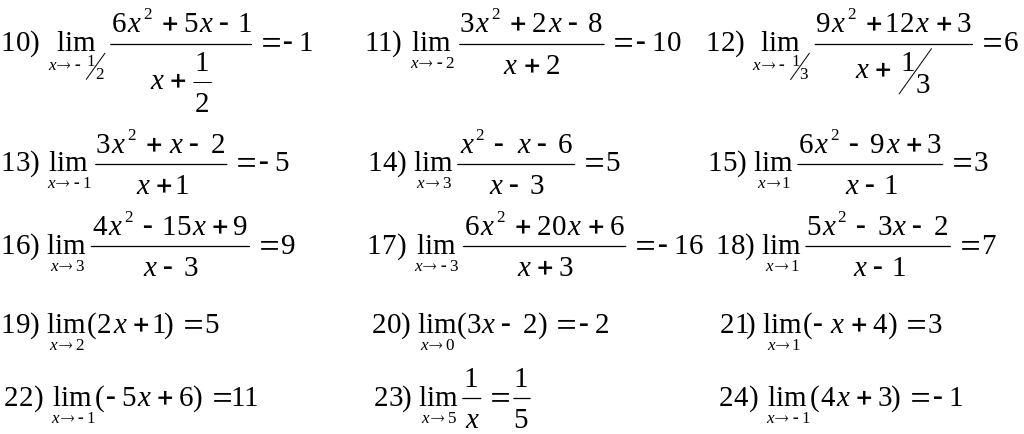
3. Доказать, что

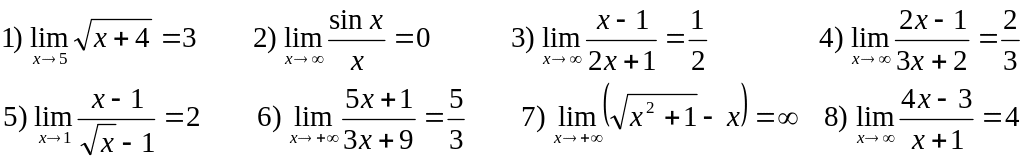
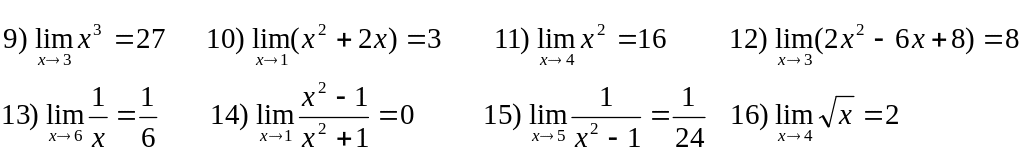
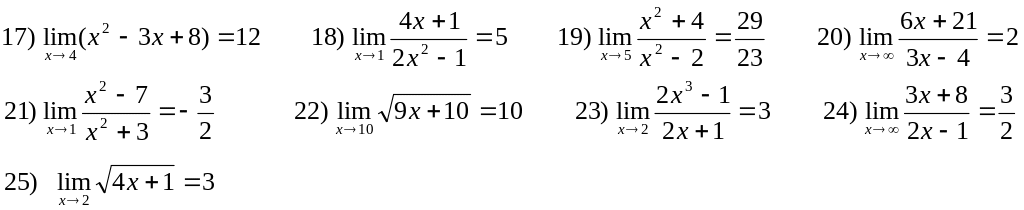
Лабораторная работа №6 Вычисление предела функции.

При вычислении предела функции необходимо знать следующие

теоремы:

Кроме того, надо пользоваться тем, что для всех основных элементарных функций в любой точке их области определения справедливо равенство:

(в силу непрерывности, Л.р. №7)

Этими простейшими пределами можно пользоваться как формулами:

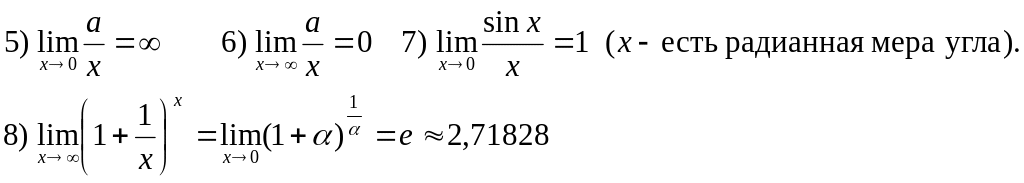
Более сложные случаи нахождения предела функции: ,[1^] рассматриваются далее в отдельности.

Пример 1.Найти предел:

Решение:

Разлагаем знаменатель на множители:

Здесь нет сокращения на нуль, что никогда недопустимо. Согласно определению предела функции аргумент х стремиться к своему предельному значению 2, никогда с ним не совпадая.

Пример 2. Найти предел:

Решение:

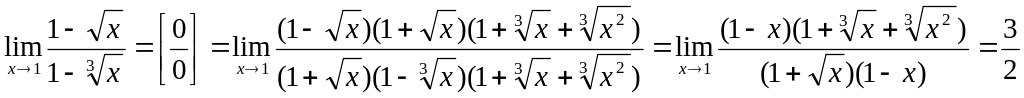Пример 3. Найти предел:

Решение:

(Применяем тригонометрическую формулу так, чтобы использовать первый замечательный предел).

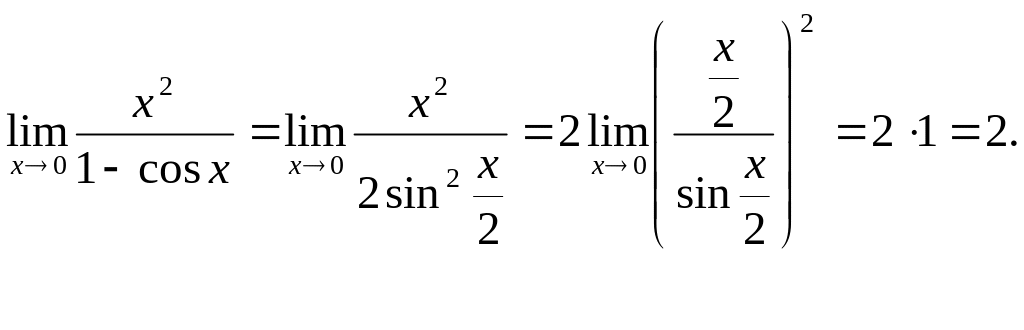
Пример 4. Найти предел:

Решение:

Деля числитель и знаменатель на наивысшую степень х (на х²), находим

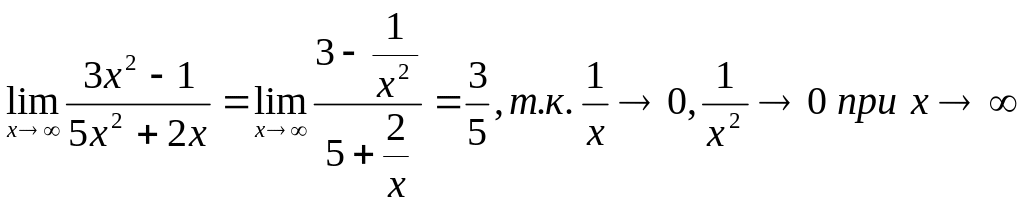
Случай, когда при ха или х функция f(x) представляет произведение бесконечно малой величины на бесконечно большую , приводится путем преобразования функции к одному из двух рассмотренных случаев, т.е. к или к .

Случай, когда при ха или х функция f(x) представляет разность двух положительных бесконечно больших величин , можно привести к случаю или путем преобразования функции к дроби.

Пример 5. Найти следующий предел:

Решение:

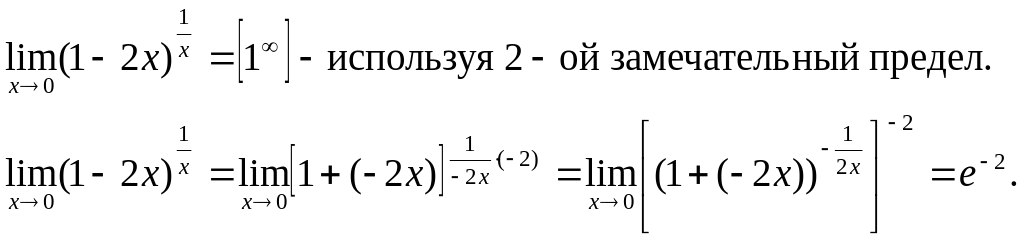
ВАРИАНТЫ.

Найти следующие пределы:

В-1

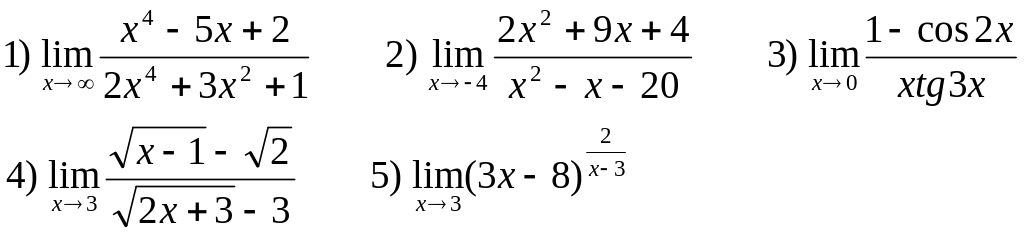
В-2

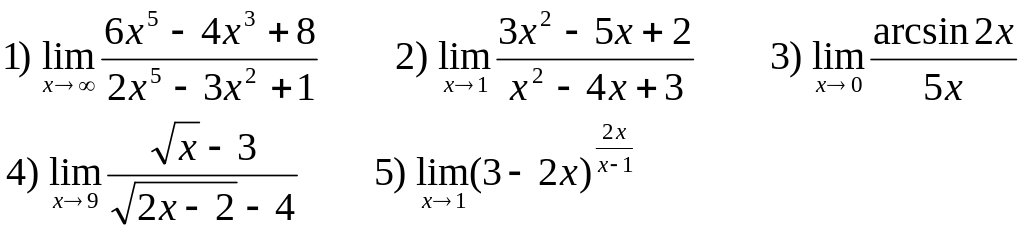
В-3

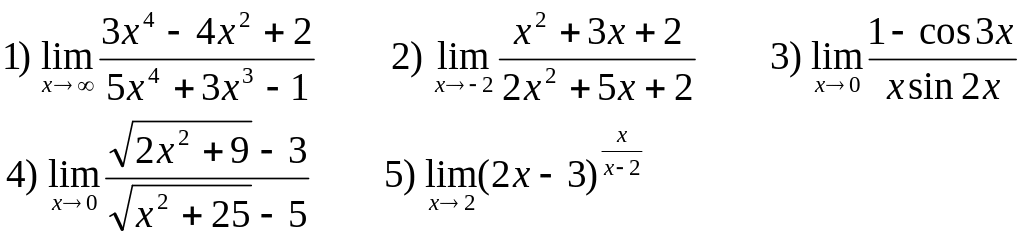
В-4

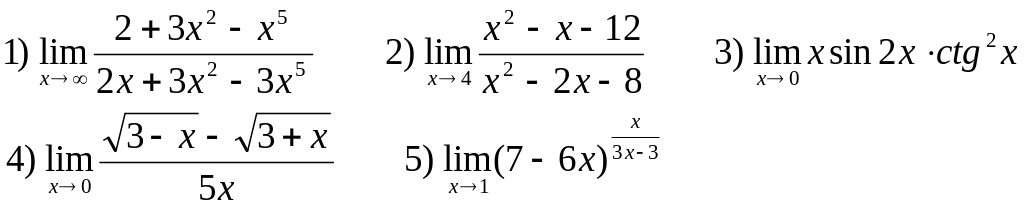
В-5

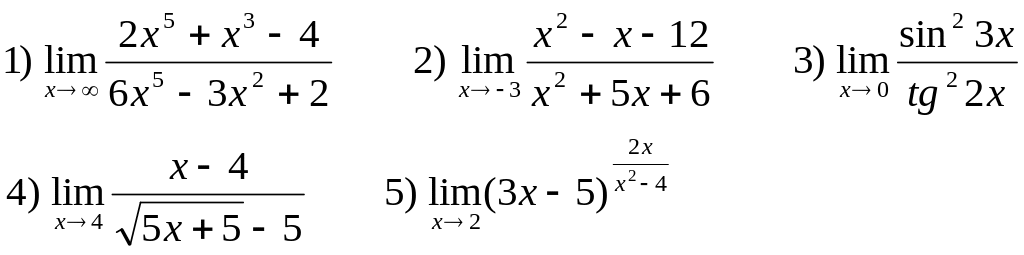
В-6

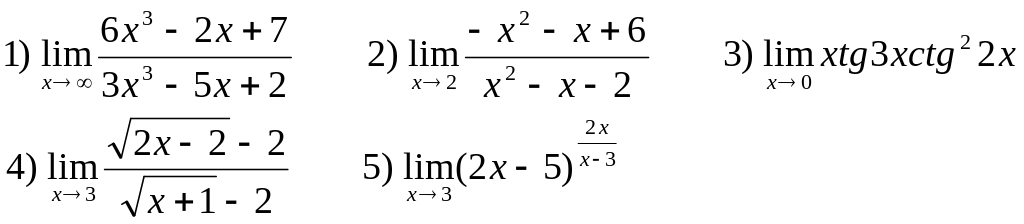
В-7

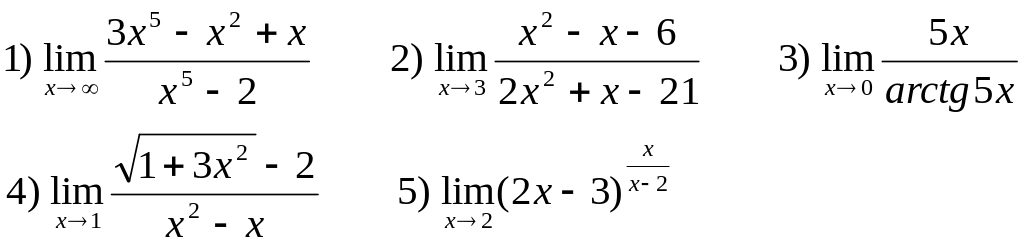
В-8

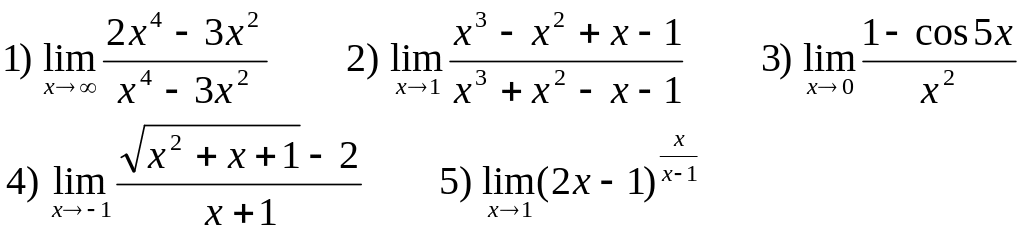
В-9

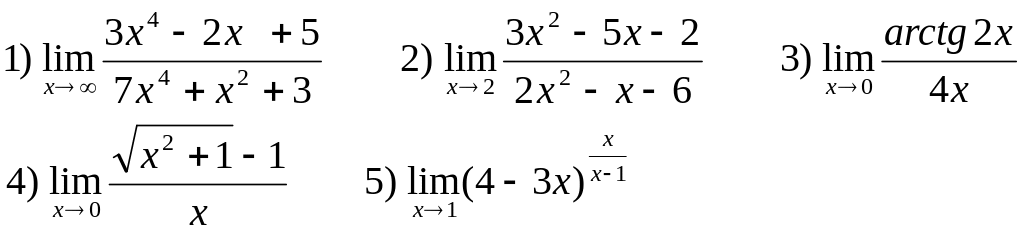
В-10

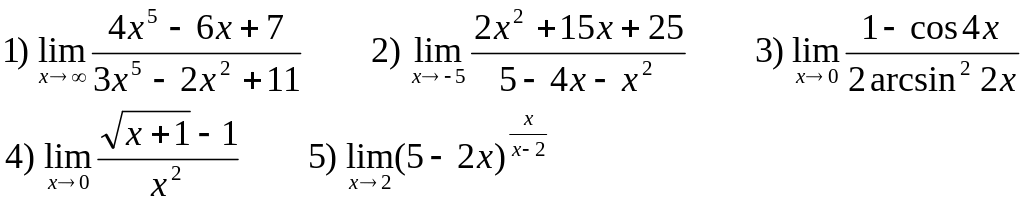
В-11

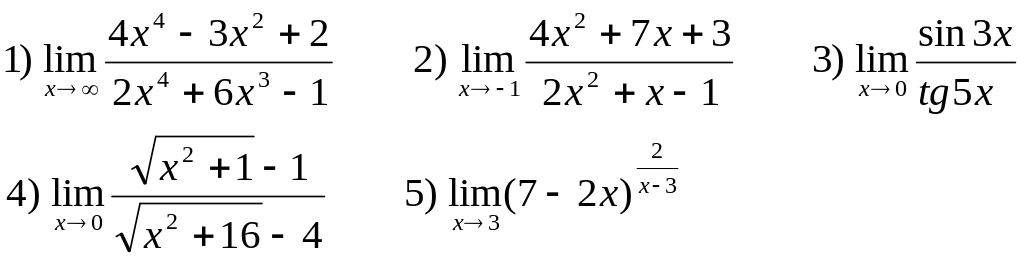
В-12

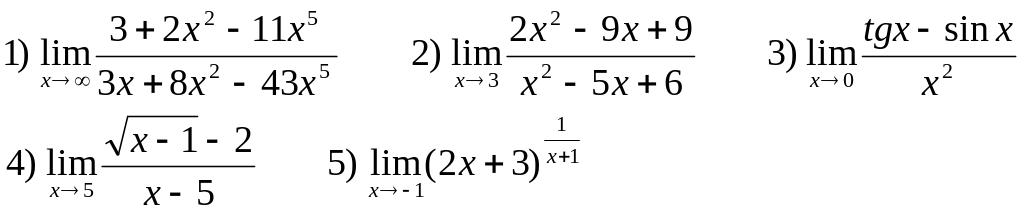
В-13

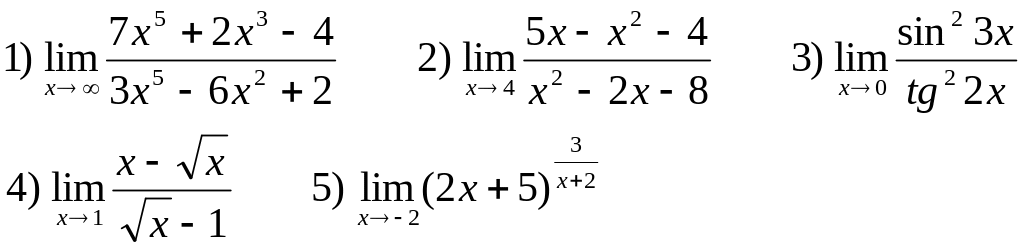
В-14

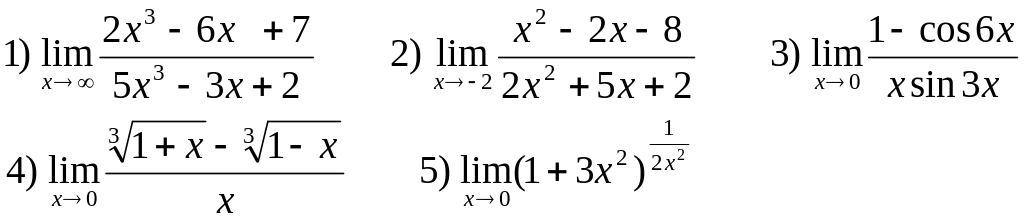
В-15

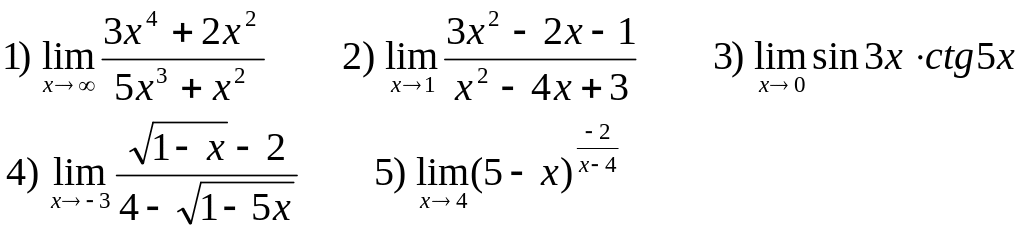
В-16

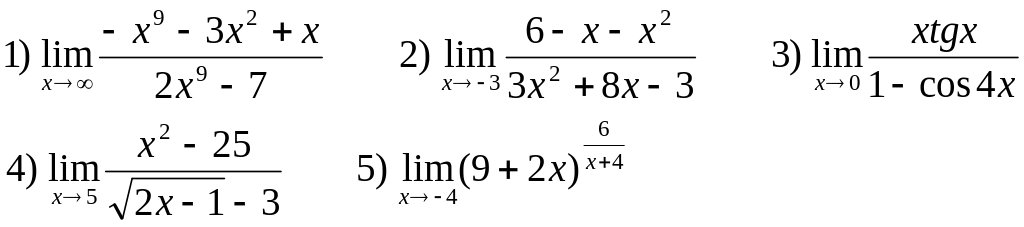
В-17

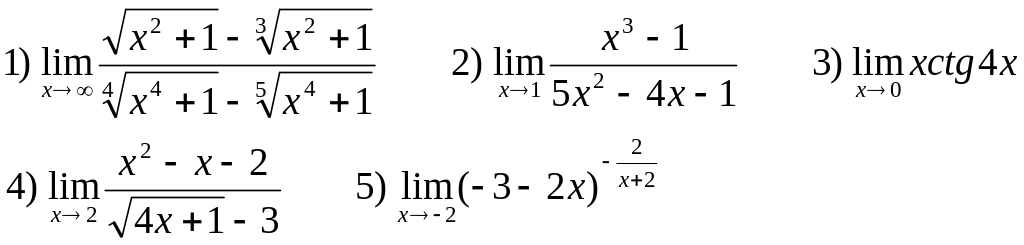
В-18

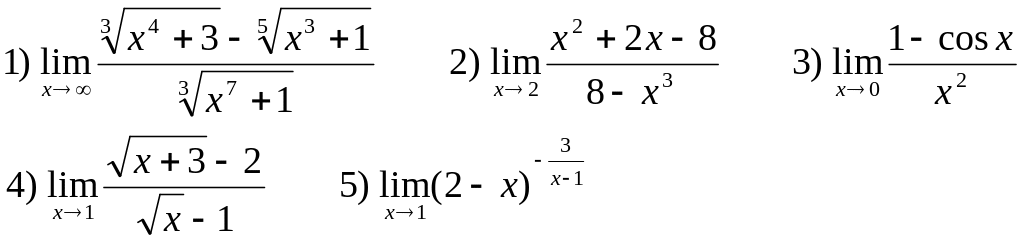
В-19

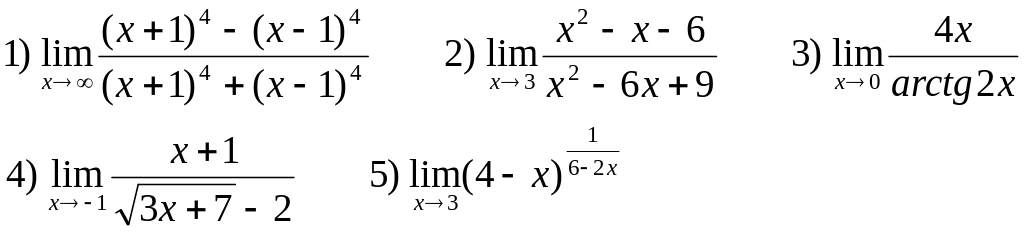
В-20

В-21

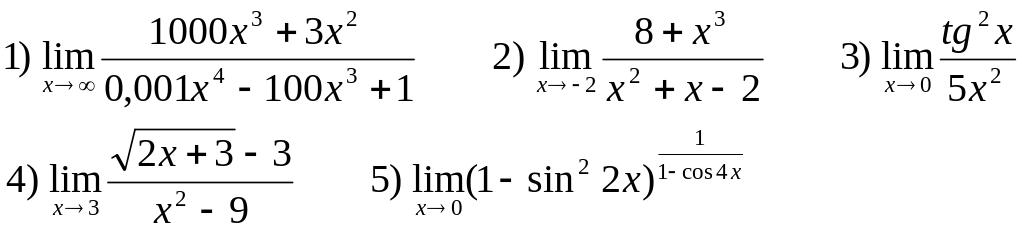
В-22

В-23

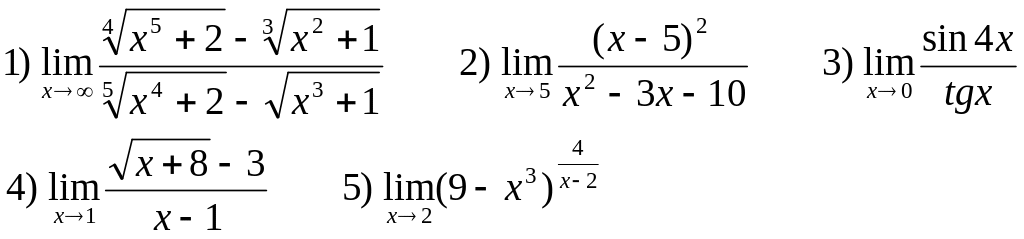
В-24

В-25