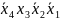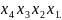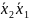- •Введение
- •1 Домашние задания «Синтез и анализ комбинационных схем»
- •1.1 Домашнее задание №1:
- •1.2 Домашнее задание №2:
- •1.3 Домашнее задание №3:
- •1.4 Варианты функций алгебры логики домашних заданий, 1-я гр.
- •1.5 Варианты функций алгебры логики домашних заданий, 2-я гр.
- •1.6 Варианты функций алгебры логики домашних заданий, 3-я гр.
- •2 Теоретические сведения, рекомендации и пояснения к выполнению домашних заданий
- •2.1 Способы задания фал
- •2.2 Правила записи фал в сднф и скнф
- •2.3 Преобразование сднф, скнф, днф и кнф фал в базисы функций и-не и или-не.
- •2.4 Риски сбоя в комбинационных схемах
- •2.5 Введение в фал стробирующего сигнала. Синхронизация сигналов
- •3 Минимизация функций алгебры логики
- •3.1 Элементарные конъюнкции и дизъюнкции.
- •3.2 Минимальные днф и кнф
- •3.3 Сокращенная и тупиковая днф (кнф)
- •3.4 Метод Квайна минимизации фал
- •3.5 Карты Карно.
- •3.6. Минимизация по методу Квайна с применением карт Карно
- •3.7 Нахождение тупиковых и минимальных днф (кнф) функции с помощью преобразования Петрика
- •3.8 Нахождение минимальных кнф фал.
- •3.9 Преобразование минимальных днф и кнф в базисы функций и-не и или-не
- •4 Экспериментальные исследования и рекомендации к практической реализации домашних заданий
- •5 Требования к отчетам о выполнении домашних заданий
- •6 Проверка выполнения домашних заданий
- •7 Контрольные вопросы
- •Заключение
- •Список литературы
- •2. Пухальский г.Н., Новосельцева т.Я. Цифровые устройства: Учеб. Пособие для втузов. – спб.: Политехника, 1996. – 885 с.:ил.
3.4 Метод Квайна минимизации фал
При минимизации по методу Квайна заданную ФАЛ f(хn,…, х1) нужно представить в СДНФ, если она не задана в этой форме.
Если ФАЛ задана в
произвольной ДНФ, то элементарные
конъюнкции с помощью операции развертывания
нужно представить в виде конституент
единицы. Операция развертывания
заключается в умножении элементарных
конъюнкций, не являющихся конституентами
единицы, на выражение типа (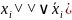 ,
где хi
– переменная, отсутствующая в записи
элементарной конъюнкции.
,
где хi
– переменная, отсутствующая в записи
элементарной конъюнкции.
Если ФАЛ задана в произвольной форме, то эту функцию всегда можно привести к табличной форме, а от нее перейти к СДНФ.
Этапы минимизации ФАЛ по методу Квайна:
1. Нахождение
сокращенной ДНФ. Для этого выполняются
операции неполного склеивания и
поглощения с целью поиска всех простых
импликант функции. Сначала попарно
сравниваются все конституенты единицы
СДНФ функции. Если какие-либо две
конституенты единицы отличаются друг
от друга только одной переменной (в
одной хi,
а в другой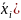 ,
то выписывают их общую часть, а против
этих конституент единицы ставят метки.
Замена двух конституент единицы вида
Aхi
и A
,
то выписывают их общую часть, а против
этих конституент единицы ставят метки.
Замена двух конституент единицы вида
Aхi
и A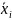 является
результатом их склеивания по аргументу
хi:
Aхi
∨
A
является
результатом их склеивания по аргументу
хi:
Aхi
∨
A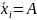 .
.
Метки означают, что отмеченные ими конституенты единицы поглощаются импликантой А. Таким образом получаются все импликанты, являющиеся конъюнкциями (n-1)-го ранга. Полученные элементарные конъюнкции (n-1)-го вновь сравнивают попарно, находят импликанты, являющиеся конъюнкциями (n-2)-го ранга, склеивающиеся конъюнкции (n-2)-го отмечают метками и т.д. Этап заканчивается, когда вновь полученные конъюнкции r-го ранга уже не склеиваются между собой. Все неотмеченные конъюнкции являются простыми импликантами. Неотмеченными могут оказаться и исходные конституенты единицы. Дизъюнкция всех простых импликант и есть сокращенная ДНФ заданной ФАЛ.
2. Нахождение существенных импликант. Задача данного этапа - определить простые импликанты, которые должны обязательно входить в минимальную ДНФ, т.е. существенные импликанты. На последующих этапах определяются простые импликанты, которые можно не включать в минимальную ДНФ.
Для поиска существенных импликант составляется таблица с числом строк, равным числу простых импликант, и числом столбцов, равным числу конституент единицы минимизируемой функции. Строки обозначают простыми импликантами, а столбцы – конституентами единицы функции. На пересечении строки с импликантой и столбца с конституентой единицы, поглощаемой этой импликантой, ставят метки.
Если в каком-либо столбце таблицы имеется только одна метка, то простая импликанта, стоящая в строке с этой меткой, является существенной импликантой. Существенная импликанта должна обязательно входить в минимальную ДНФ, так как она является единственной простой импликантой, которая поглощает данную конституенту единицы. Поэтому из таблицы исключаются строки, соответствующие существенным импликантам, и столбцы конституент единицы, поглощаемых этими существенными импликантами.
3. Исключение лишних столбцов и строк. Анализируется таблица, полученная после выполнения второго этапа. Если в ней имеются два столбца, содержащие метки в одних и тех же строках, то один из столбцов можно исключить. Это возможно потому, что одна из импликант, которая поглощает конституенты единицы оставшегося и исключенного столбцов, будет включена в минимальную ДНФ функции.
Если после исключения некоторых столбцов в таблице появятся строки, не содержащие меток, то простые импликанты, соответствующие этим строкам, исключаются из дальнейшего рассмотрения, так как они не поглощают оставшиеся конституенты единицы.
4. Выбор минимальной ДНФ. Анализируя таблицу, полученную после выполнения третьего этапа, выбирают совокупность простыхимпликант, которые перекрывают своими метками все столбцы таблицы. Возможны несколько вариантов такого выбора. Дизъюнкция простыхимпликант этой совокупности и существенных импликант, полученных при выполнении второго этапа, является тупиковой ДНФ минимизируемой функции. Число различных тупиковых форм равно числу выбранных совокупностей простых импликант, полученных при выполнении этого этапа. Из тупиковых форм выбирают минимальную ДНФ функции, т.е. тупиковую форму, имеющую минимальное число букв. Минимальных форм может быть несколько.
Пример 6. Найти минимальную ДНФ функции
f(х4,х3,х2,х1)=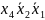 ∨
∨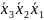 ∨
∨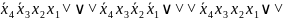
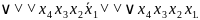
Так как функция
задана в виде произвольной ДНФ, то
приведем ее к СДНФ, умножив первую
конъюнкцию функции на (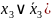 ,
вторую – на (
,
вторую – на (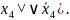 Тогда получим:
Тогда получим:
f(х4,х3,х2,х1)=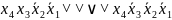 ∨
∨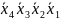 ∨
∨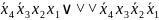 ∨
∨
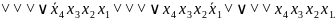
Решение.
1. Найдем простые импликанты.
Конституенты единицы (элементарные конъюнкции 4-го ранга):
1)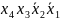 *, 2)
*, 2)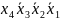 *,
3)
*,
4)
*,
3)
*,
4)
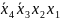 *,
*,
5)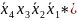 6)
6)
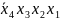 *,
7)
*,
7)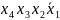 *,
8)
*,
8)
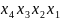 *.
*.
Сравнивая первую конституенту единицы списка с последующими, затем вторую с последующими и т.д.,находим пары конституент единицы, которые отличается только одной переменной. Такие конъюнкции склеиваются по этой переменной. После выполнения всех сравнений получим элементарные конъюнкции 3-го ранга:
1)
*,
2)
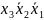 *,
3)
*,
3)
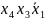 , 4)
*,
, 4)
*,
5)
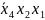 ,
6)
,
6)
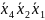 *,
7)
*,
7)
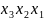 , 8)
, 8)
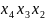 .
.
Сравнивая
элементарные конъюнкции 3-го ранга, а,
именно, первую с последующими, вторую
с последующими и т.д., получим элементарную
конъюнкцию 2-го ранга
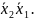 На этом процесс сравнения закончен.
Простыми импликантами являются
конъюнкции, не отмеченные знаком «*»:
На этом процесс сравнения закончен.
Простыми импликантами являются
конъюнкции, не отмеченные знаком «*»: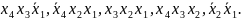 Знак «*» означает, что конъюнкции,
отмеченные этим знаком, поглощаются
другими конъюнкциями, не отмеченные
этим знаком. Дизъюнкция всех простых
импликант – это сокращенная ДНФ.
Знак «*» означает, что конъюнкции,
отмеченные этим знаком, поглощаются
другими конъюнкциями, не отмеченные
этим знаком. Дизъюнкция всех простых
импликант – это сокращенная ДНФ.
2. Найдем существенные импликанты функции, для чего составим импикантную таблицу. ФАЛ содержит восемь конституент единицы и имеет пять импликант. Поэтому импликантная таблица содержит восемь столбцов и пять строк с метками, определяющими вхождение конституент единицы в соответствующие импликанты функции (табл. 2).
Таблица 2
Конст. ед. Пр. импл. |
|
|
|
|
|
|
|
|
|
|
* |
|
|
|
|
|
* |
|
|
|
|
|
|
* |
|
* |
|
|
|
|
|
|
|
|
|
* |
|
* |
|
|
|
|
|
|
|
|
* |
* |
|
|
* |
* |
* |
|
* |
|
|
|
|
Существенными
импликантами являются конъюнкции
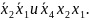 Поэтому из табл. 2 исключаем строки,
соответствующие этим импликантам, и
столбцы 2, 3, 4, 5, 6, 7 конституент единицы,
поглощаемых этими импликантами. Тогда
получим табл. 3.
Поэтому из табл. 2 исключаем строки,
соответствующие этим импликантам, и
столбцы 2, 3, 4, 5, 6, 7 конституент единицы,
поглощаемых этими импликантами. Тогда
получим табл. 3.
Таблица 3
-
Конституента
единицы
Простая
импликанта
*
*
*
*
3. Лишних столбцов
и строк в ней нет. Оставшиеся в табл.3
конституенты единицы могут быть
представлены в тупиковых ДНФ импликантой
или дизъюнкцией импликант
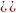 ∨
∨
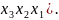
4. Тупиковыми ДНФ являются:
fтуп1(х4,
х3,
х2,
х1)
=
∨
∨
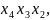
fтуп2(х4, х3, х2, х1) = ∨ ∨ ∨ .
Минимальной формой данной ФАЛ является
fмин(х4,
х3,
х2,
х1)
=
∨
∨
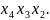
Последний этап может быть и простым, и очень сложным. Поэтому для выполнения этого этапа в случае сложности выбора всех совокупностей простых импликант можно рекомендовать метод Петрика, позволяющий аналитически найти все тупиковые и все минимальные ДНФ.
При большом числе переменных трудоемкость метода Квайна возрастает, что связано с необходимостью полного попарного сравнения всех конъюнкций при нахождении простых импликант. Метод Квайна-Мак-Класки упрощает поиск простых импликант за счет уменьшения числа сравнений. Однако более эффективным при числе переменных 4-6 является применение карт Карно для нахождения простых и существенных импликант. Таким образом упрощается выполнение первого и второго этапов метода Квайна.
Метод Квайна с применением карт Карно и преобразования Петрика позволяет найти все тупиковые и все минимальные формы ФАЛ аналитически, исключив этап выбора простых импликант для покрытия всех столбцов импликантной таблицы ФАЛ.