Занятие № 8. Формула Байеса.
Задания:
1. На вход радиолокационного устройства с вероятностью 0,8 поступает смесь полезного сигнала с помехой, а с вероятностью 0,2 – только помеха. Если поступает полезный сигнал с помехой, то устройство регистрирует наличие какого-то сигнала с вероятностью 0,7; если только помеха, - то с вероятностью 0,3. Известно, что устройство зарегистрировало наличие какого-то сигнала. Найти вероятность того, что в его составе есть полезный сигнал.
2. Число грузовых автомашин, проезжающих по шоссе, на котором стоит бензоколонка, относится к числу легковых машин, проезжающих по тому же шоссе как 3:2. Вероятность того, что будет заправляться грузовая машина, равна 0,1; для легковой машины эта вероятность равна 0,2. К бензоколонке подъехала для заправки машина. Найти вероятность того, что это грузовая машина.
3. В урне находится шар неизвестного цвета – с равной вероятностью белый или черный. В урну опускается один белый шар и после тщательного перемешивания наудачу извлекается один шар. Он оказался белым. Какова вероятность того, что в урне остался белый шар.
4. В группе из 25 человек, пришедших сдавать экзамен по теории вероятностей, имеется 10 отличников, 7 подготовленных хорошо, 5 – удовлетворительно и 3 человека плохо подготовлены. Отличники знают все 25 вопросов программы, хорошо подготовленные – 20, подготовленные удовлетворительно – 15, и плохо подготовленные – 10. Вызванный наудачу студент ответил на два заданных вопроса. Найти вероятность того, что студент подготовлен удовлетворительно.
5. Имеются три партии по 20 деталей. В одной – две бракованных, в другой – четыре, в третье – шесть. Извлеченные случайным образом из какой-то партии две детали оказались бракованными. Какова вероятность, что это была первая партия?
6. Три стрелка
производят по одному выстрелу в одну и
ту же мишень. Вероятности попадания в
мишень при одном выстреле для каждого
из стрелков соответственно равны
,
,
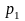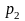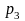.Какова
вероятность того, что второй стрелок
промахнулся, если после выстрелов в
мишени оказалось две пробоины?
7. Два охотника пошли на охоту, увидели медведя и одновременно выстрелили. Медведь убит, но на шкуре одна дыра, то есть попал только один из охотников. У первого вероятность попадания 0,8, у второго – 0,4. Шкуру продали за 70 рублей. Как поделить деньги между охотниками?
Занятие № 9. Схема Бернулли.
Задания:
1. Монету бросают пять раз. Найти вероятность того, что «герб» выпадет: а) два раза; б) менее двух раз; в) не менее двух раз.
2. В семье пять детей. Найти вероятность того, что среди этих детей: а) два мальчика; б) не более двух мальчиков; в) более двух мальчиков; г) не менее двух и не более трех мальчиков. Вероятность рождения мальчика принять равной 0,51.
3. Отрезок АВ разделен точкой С в отношении 2:1. На этот отрезок наудачу брошены четыре точки. Найти вероятность того, что две из них окажутся левее точки С и две—правее. Предполагается, что вероятность попадания точки на отрезок пропорциональна длине отрезка и не зависит от его расположения.
4. Вероятность хотя бы одного появления события при четырех независимых опытах равна 0,5904. Какова вероятность появления события при одном опыте, если при каждом опыте эта вероятность одинакова?
5. Сколько нужно взять случайных цифр от 0 до 9, чтобы цифра 7 появилась хотя бы один раз с вероятностью не меньшей 0,9?
6. Найти наивероятнейшее число успехов в схеме Бернулли с n испытаниями при данной вероятности успеха p.
7. Вероятность получения удачного результата при производстве химического опыта равна 2/3. Найти наивероятнейшее число удачных опытов, если их общее количество равно 7.
8. Вероятность попадания в цель при каждом выстреле из орудия равна 0,8. Сколько нужно сделать выстрелов, чтобы наивероятнейшее число попаданий было равно 20?
9. Пусть вероятность того, что студент опоздает на лекцию, равна 0,08. Найти наиболее вероятное число опоздавших из 96 студентов и вероятность этого числа опоздавших.
10. Найти вероятность того, что событие А наступит ровно 70 раз в 243 испытаниях, если вероятность появления этого события в каждом испытании равна 0,25.
11. Вероятность рождения мальчика равна 0,51. Найти вероятность того, что среди 100 новорожденных окажется: а) 50 мальчиков; б) больше мальчиков, чем девочек.
12. Найти вероятность одновременной остановки от 20 до 35 машин из работающих 100 машин, если вероятность остановки для одной машины равна 0,2.
13. В партии смешаны детали двух сортов: 80% первого сорта и 20% второго сорта. Сколько деталей первого сорта с вероятностью 0,0967 можно ожидать среди 100 наудачу взятых деталей?
14. Произведено 600 независимых испытаний с вероятностью появления ожидаемого результата 0,6 в каждом испытании. Какой должна быть абсолютная частота появления ожидаемого результата, чтобы вероятность появления такой частоты была равна 0,0045?
15. На некотором предприятии доля брака составляет в среднем 0,2%. Какова вероятность того, что на этом предприятии в партии, состоявшей из 500 изделий, окажется: а) три изделия бракованных; б) не более четырех изделий бракованных; с) хотя бы одно изделие бракованное.
16. Завод отправил на базу 1000 изделий. Вероятность повреждения изделия в пути равна 0,002. Найти вероятность того, что в пути будет повреждено: а) ровно три; б) менее трех; с) более трех; д) хотя бы одно изделие.
17. Костя Сидоров любит ходить в тир пострелять. Его рекорд в серии из пяти выстрелов составляет 47 очков. какова вероятность повторить рекорд, если в среднем он попадает в десятку в 30% случаев, в девятку - в 50%, в восьмерку - в 10%, в семерку - в 5%, оставшиеся 5% приходятся на диапазон 0-6?