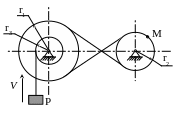
Приклад 3.

Д ано:

m = 160 кг,

S = 0,7t ²,

S₁ = 4,9 м,

r₁ = 0,35 м,

r₂ = 0,24 м,

r₃ = 0,08 м.

V_P1 - ? a _P1 - ?

_Б1 - ? _Б1 - ?

_ПР1 - ? _ПР1 - ?

V_М1 - ? а_М1 - ?

Т - ?

Визначаємо час, коли вантаж пройде шлях S₁ = 4,9 м:

S₁ = 0,7 t₁ ², 4,9 = 0,7 t₁ ²,

t₁ ² = 7, .

Швидкість вантажу обчислюється за виразом:

.

Швидкість вантажу в момент часу t₁ = 2,65 c буде:

.

Прискорення вантажу:

.

Прискорення вантажу не залежить від часу, тому .

Вал барабана буде обертатись при підйомі вантажу за годинниковою стрілкою. Так само (згідно зі схемою) буде обертатись і вал приводу з колесом радіуса r₃.

Всі наступні величини знайдемо для моменту часу .

Кутова швидкість вала барабана радіуса r₁ дорівнює:

.

Така сама буде і кутова швидкість колеса радіусом r₂.

Кутове прискорення вала барабана буде:

– від часу не залежить.

Передаточне число передачі згідно схеми (будь то ланцюгова, або пасова передача):

.

Це означає, що колесо радіусом r₃ (привід) буде обертатися в три рази швидше, ніж колесо радіуса r₂.

Кутова швидкість вала приводу радіуса r₃ :

.

Кутове прискорення вала приводу:

.

Швидкість точки М в момент часу буде дорівнювати:

.

Визначимо прискорення точки М.

Воно складається з тангенційного і нормального прискорень.

, спрямовано по дотичній, в бік швидкості;

, спрямовано по радіусу до центра.

Повне прискорення точки М буде дорівнювати:

.

Для визначення натягу троса складаємо диференціальне рівняння руху вантажу. Оберемо напрям осі „х” у той бік, куди рухається вантаж (тобто вгору). На вантаж діють сили: вага P = mg і натяг тросу Т.

Рівняння руху: .

Прискорення вантажу: .

Тоді:

.

0 1

2 3

4 5

6 7

8 9

Рисунок 3.

Задача 4.

Механічна система складається з двох тіл масою m₁ і m₂, з’єднаних між собою тросом, перекинутим через блок. Нехтуючи масою блоків і масою троса, визначити швидкість маси m₁, коли вона пройде шлях S₁. Спочатку система знаходилася в стані спокою.

При розрахунках прийняти:

• радіус катка r = 0,2 м, каток суцільний;

• коефіцієнт тертя ковзання f = 0,2;

• коефіцієнт тертя кочення k = 0,01.

Таблиця 4.

Дано	Передостання цифра шифру
	0	1	2	3	4	5	6	7	8	9
m1, кг	100	120	140	160	180	200	180	160	140	120
m2, кг	40	60	80	100	120	140	100	80	60	40
S1, м	1,0	1,2	1,4	1,6	1,8	2,0	2,2	2,6	2,6	2,8