Глава 7. Неопределенный интеграл
§1. Понятие неопределенного интеграла
В дифференциальном исчислении решается задача:
По данной функции F(x) найти её производную (или дифференциал):
F’(x) или dF(x) = F’(x)dx.
В интегральном исчислении решается обратная задача:
Найти функцию F(x), зная её производную F’(x) = f (x) или дифференциал
dF(x) = f (x)dx.
Искомую функцию F(x) называют первообразной функции f(x).
Прямая
задача:
Обратная
задача:
Определение.Функция F(x)
называется первообразной
функции f(x)
на интервале (а,b),
если для любого
выполняется условие F’(x)=f(x)
(или dF(x)=f(x)dx)
(1)
Например:1)
2)
3)
Очевидно, что если F(x)
– первообразная для функции f(x)
на интервале (a,b),
то функция F(x)
+ C, где C=const,
также первообразная для функции f(x)
на этом же интервале:
.
Отсюда следует, что если функция f(x) имеет хотя бы одну первообразную на интервале (a,b), то она будет иметь б/м первообразных на этом интервале.
Можно показать, что справедлива следующая теорема:
Теорема. Если функция F(x) является первообразной функции f(x) на интервале (a,b), то множество всех первообразных для f(x) задается формулой F(x) + C, где C- константа.
Доказательство:
Пусть Ф(x)
некоторая другая, отличная от F(x)
первообразная функции f(x),
т.е. Ф’(x) = f(x).
Тогда для всех
имеем (Ф(x) –
F(x))’=
Ф’(x) – F’(x)
= f(x)
– f(x)
= 0
Ф(x) – F(x)
= C, где С –
константа.
Следовательно: Ф(x) = F(x) + C ч.т.д.
Определение.Множество
всех первообразных для функции f(x)
F(x)
+ C называется
неопределенным интегралом от функции
f(x)
и обозначается
-
знак интеграла
f(x) – подинтегральная функция
f(x)dx – подинтегральное выражение
х – переменная интегрирования
Операция нахождения неопределенного интеграла от функции называется интегрированием этой функции.
Геометрически неопределенный интеграл представляет собой семейство «параллельных» кривых y = F(x) + C.
График каждой первообразной называется интегральной кривой.
Например,
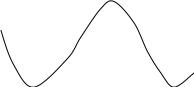y c1=1
Y=sinx+1
1 c=0
0
x
Y=sinx
-1
c2=-1
Y=sinx-1
Замечание:
Для всякой ли функции существует неопределенный интеграл?
Имеет место теорема, утверждающая, что «всякая непрерывная на (a,b) функция имеет на этом интервале первообразную», а, следовательно, и неопределенный интеграл.
Итак, , где F’(x) = f (x) и dF(x) = f (x)dx..
Из этого определения неопределенного интеграла вытекают следующие свойства: