Цепи постоянного тока Структура электрической цепи

Электрической цепью называется совокупность соединенных друг с другом источников электрической энергии и приемников электрической энергии (потребителей, нагрузок).

Источники называют активными, а приемники – пассивными элементами цепи.

Постоянным током называется ток, неизменный во времени.

Постоянный ток обозначается буквой I, ЭДС источника – Е, сопротивление – R . В международной системе единиц (СИ) ток измеряется в амперах (А), ЭДС – в вольтах (В), сопротивление – в омах (Ом).

Графически электрическую цепь изображают в виде так называемой схемы замещения, на которой элементы цепи показывают условно: источник – окружностью со стрелкой внутри, которая указывает положительное направление ЭДС или тока, сопротивление – прямоугольником, соединительные провода – отрезками прямых.

Приемник энергии и провода, соединяющие приемник с источником, называют внешней частью электрической цепи, или внешней цепью. Во внешней цепи ток течет от плюса источника к минусу, а внутри источника – от минуса к плюсу.

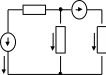
Электрические цепи бывают неразветвленными и разветвленными. В неразветвленной цепи ток во всех её элементах (участках) один и тот же. Если же цепь содержит участки с различными токами (рис.1,а), она называется разветвленной. При расчете разветвленных цепей пользуются понятиями узел, ветвь, контур цепи.

Узел цепи – это такая её точка, в которой сходятся не менее трех токов. На рис.1,а точки 1 и 2 являются узлами. Если в местах пересечения двух линий на электрической схеме поставлена точка, то в этом месте есть электрическое соединение двух линий (рис.1,б), если точки (рис.1,в) нет – нет и электрического соединения.

3 1 E₂ 4

R₁

Е₁ I₂ R₂ I₃ R₃

I₁ б) в)

2

а)

Рис. 1. Электротехническая цепь

Ветвь – это участок цепи, заключенный между двумя узлами, на всем протяжении которого ток один и тот же. Схема рис.1.а содержит три ветви: 1-3-2, 1-2, 1-4-2.

Контур – замкнутая часть схемы, которая представляет собой неразветвленную цепь, если отключить все не входящие в нее ветви. В цепи рис. 1.а можно выделить контуры 1-2-3-1, 1-4-2-1, 1-4-2-3-1.

Основные законы электрических цепей постоянного тока

В замкнутой цепи под действием ЭДС источника возникает ток I, который на сопротивлениях участков цепи создает разность потенциалов – падение напряжения.

Соотношение между током, напряжением и сопротивлением участка цепи выражается законом Ома для участка цепи

I = ,

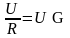где G – проводимость рассматриваемого участка цепи.

Зависимость между ЭДС источника Е, током цепи I и ее общим сопротивлением выражается законом Ома для цепи в целом.

I = ,

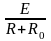где R₀ - внутреннее сопротивление источника .

Из последнего выражения напряжение на зажимах источника

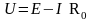
т.е. напряжение U на зажимах источника меньше его ЭДС Е на величину внутреннего падения напряжения

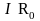
Если разветвленная цепь содержит источники в нескольких ветвях, режим ее работы не может быть описан только законом Ома. В этом случае возникает необходимость использовать законы Кирхгофа.

Первый закон справедлив для узлов цепи и формулируется так:

в любом узле электрической цепи алгебраическая сумма токов равна нулю, т.е.

.

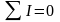При записи этого уравнения токи, приходящие к узлу учитываются со знаком плюс, отходящие от узла – со знаком минус.

Например, для узла 1 электрической схемы на рис.1.а уравнение первого закона Кирхгофа запишется следующим образом:

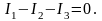
Второй закон Кирхгофа справедлив для замкнутых контуров и устанавливает связь между ЭДС, токами и сопротивлениями данного контура:

в любом замкнутом контуре алгебраическая сумма ЭДС равна алгебраической сумме падений напряжения на сопротивлениях всех его участков, т.е.

.

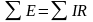В это уравнение ЭДС и токи, совпадающие с произвольно выбранным обходом контура, представляются со знаком плюс, а противоположно направленные – со знаком минус.

Например, для контура 2-3-1-4-2 схемы, изображенной на рис.1.а, уравнение второго закона Кирхгофа запишется так: .
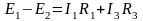