Лабораторна робота №1

Тема: «Чисельне розв’язання граничної задачі для звичайного диференціального рівняння другого порядку».

Теоретичні відомості

1. Попередні зауваження. Лінійне диференціальне рівняння другого порядку має наступний вид

(1)

Гранична задача полягає у відшуканні розв’язання рівняння (1) на відрізку [а, b], що задовольняє на кінцях відрізку умовам

(2)

Граничні умови можуть бути задані у вигляді (2), але і в більш загальному вигляді:

(3)

Методи розв’язання граничних задач досить різноманітні — це і точні аналітичні методи, і наближені, і чисельні.

Аналітичні методи вивчаються в курсі диференціальних рівнянь. Вони є лише для розв’язання вузького класу рівнянь. Зокрема, добре розвинений цей апарат для розв’язання лінійних диференціальних рівнянь другого порядку з постійними коефіцієнтами, які широко використовуються в дослідженні різних фізичних процесів (наприклад, в теорії коливань, динаміці твердого тіла і т. п.).

Наближені методи розроблялися ще задовго до появи комп'ютерів. Проте багато з них і до цих пір не втратили свого значення. Це методи колокацій, найменших квадратів та інші, засновані на мінімізації нев’язки рівнянь. Вельми ефективними є також метод Галеркіна і його модифікації. Розглянемо суть наближених методів.

Для відшукання наближеного розв’язку рівняння (1) з граничними умовами (3) вибирається деяка лінійно незалежна (базисна) система функцій, що двічі диференціюються . При цьому задовольняє граничним умовам (3), а — умовам (3) з нульовими правими частинами А, В. Шуканий наближений розв’язок представляється у вигляді лінійної комбінації базисних функцій:

(4)

Підставляючи цей вираз в рівняння (1), можна знайти різницю між його лівою і правою частинами, яка називається нев'язкою. Вона є функцією змінної х і параметрів і має вигляд

(5)

Коефіцієнти прагнуть підібрати так, щоб нев'язка була в якомусь сенсі мінімальною. Спосіб визначення цих коефіцієнтів і характеризує той або інший наближений метод.

У методі коллокацій вибираються п точок , які називають точками коллокацій, нев'язка (5) в яких прирівнюється нулю. Виходить система п лінійних алгебраїчних рівнянь відносно . Розв’язуючи дану систему, можна знайти ці коефіцієнти, які потім підставляються у розв’язок (4).

Метод найменших квадратів заснований на мінімізації суми квадратів нев’язки в заданій системі крапок . З цієї умови також виходить система лінійних алгебраїчних рівнянь відносно .

У основі методу Галеркіна лежить вимога ортогональності базисних функцій до нев’язки яке виражається у вигляді

З цих умов також виходить система лінійних алгебраїчних рівнянь щодо коефіцієнтів лінійної комбінації (4).

Аналогічно будуються деякі інші наближені методи. Всі вони зводяться до побудови системи лінійних алгебраїчних рівнянь, з якої, якщо існує її розв’язок, знаходяться невідомі коефіцієнти. Вони потім використовуються для побудови розв’язку як лінійної комбінації базисних функцій.

2. Метод стрілянини. Розглянемо граничну задачу для рівняння другого порядку, дозволеного щодо другої похідної:

(6)

Шукатимемо розв’язок цього рівняння на відрізку [0,1]. Будь-який відрізок [а, b] можна привести до цього відрізка за допомогою заміни змінної

Граничні умови на кінцях даного відрізку приймемо в простому вигляді (2), тобто

(7)

Суть методу стрілянини полягає в зведенні розв’язання граничної задачі (6), (7) до розв’язання послідовності завдань Коші для того ж рівняння (6) з початковими умовами

(8)

Де — точка на оси ординат, в якій знаходиться початок шуканої інтегральної кривої; —кут нахилу дотичної до інтегральної кривої в цій точці (рис.1). Так як розв’язок задачі Коші залежить від параметру , будемо шукати таку інтегральну криву , яка виходить з точки (0, ) та потрапляє у точку (1, ). Таким чином, якщо , то розв’язок задачі Коші співпаде з розв’язком граничної задачі. При х = 1, враховуючи другу граничну умову (7), отримаємо , або

(9)

Рисунок - 1 Метод стрілянини

Отже, для знаходження параметра отримаємо рівняння вигляду де . Це рівняння відрізняється від звичного запису тим, що функцію F(x) не можна представити у вигляді деякого аналітичного виразу, оскільки вона є розв’язанням задачі Коші (6) (8). Проте для розв’язання рівняння (9) може бути використаний будь-якому з розглянутих раніше методів розв’язання нелінійних рівнянь.

Наприклад, при використанні метода ділення відрізку пополам по­ступаем следующим образом. Находим начальный отрезок [ ], со­держащий значение , на концах которого функция F(x) принимает значения разных знаков. Для этого решение задачи Коши долж­но при х = 1 находиться ниже точки , а — выше. Далее, полагая , снова решаем задачу Коші при и в соответствии с методом деления отрезка пополам отбрасываем один из отрезков: [ ] или [ ], на котором функция F(x) не меняет знак, и т. д. Процесс поиска решения прекращает­ся, если разность двух последовательно найденных значений меньше некоторого наперед заданного малого числа. В этом случае полученное последним решение задачи Коши и будет принято за искомое решение краевой задачи.

Описаний алгоритм називається методом стрілянини цілком виправдано, оскільки в нім як би проводиться «пристрілка» по куту нахилу інтегральної кривої в початковій точці. Слід зазначити, що цей алгоритм добре працює в тому випадку, якщо розв’язання не дуже чутливо до змін ; інакше ми можемо зіткнутися з нестійкістю.

Для розв’язання рівняння (9) використовуються і інші методи. Зокрема, одним з найнадійніших є метод Ньютона. Його застосування полягає в наступному. Хай — початкове наближення до . Побудуємо ітераційний процес для знаходження подальших наближень за допомогою формули методу Ньютона:

З урахуванням того, що маємо

(10)

Похідну в знаменнику цього виразу можна знайти чисельно:

(11)

Тут — довільне мале обурення .

Для обчислення правої частини (11) потрібно розв’язати задачу Коші при внаслідок чого знайдемо значення . Потім по формулі (10) знаходимо наступне наближення параметра і так далі Цей ітераційний процес продовжується до тих пір, поки два послідовні наближення і не почнуть відрізнятися менше, ніж на задане мале число .

Алгоритм розв’язання граничної задачі методом стрілянини із застосуванням пристрілки по методу Ньютона представлений на рис.2. Знаходження розв’язання задачі Коші входить в даний алгоритм як окремий модуль з вхідним даним . На виході модуля виходить розв’язання у вигляді значень у крапках де .

Методи стрілянини можуть також використовуватися для розв’язання системи рівнянь. В цьому випадку граничні задачі (а не задачі Коші) може виникнути внаслідок того, що значення однієї частини шуканих функцій задані при одному значенні незалежної змінної (наприклад, при х = 0), а інший — при іншому (наприклад, х =1). Тоді «пристрілка» проводиться по невідомих значеннях шуканих функцій при х = 0 до тих пір, поки не задовольнятимуться відповідні граничні умови при х = 1.

Введення
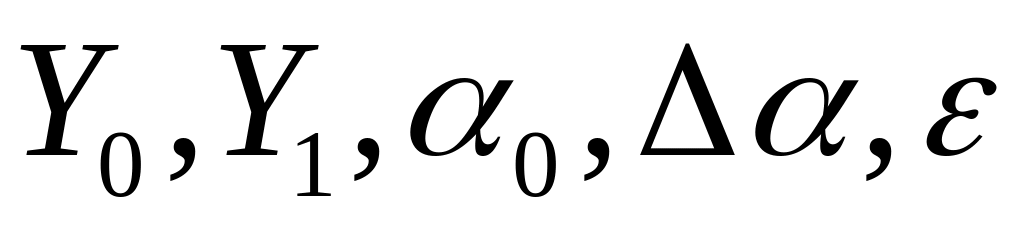
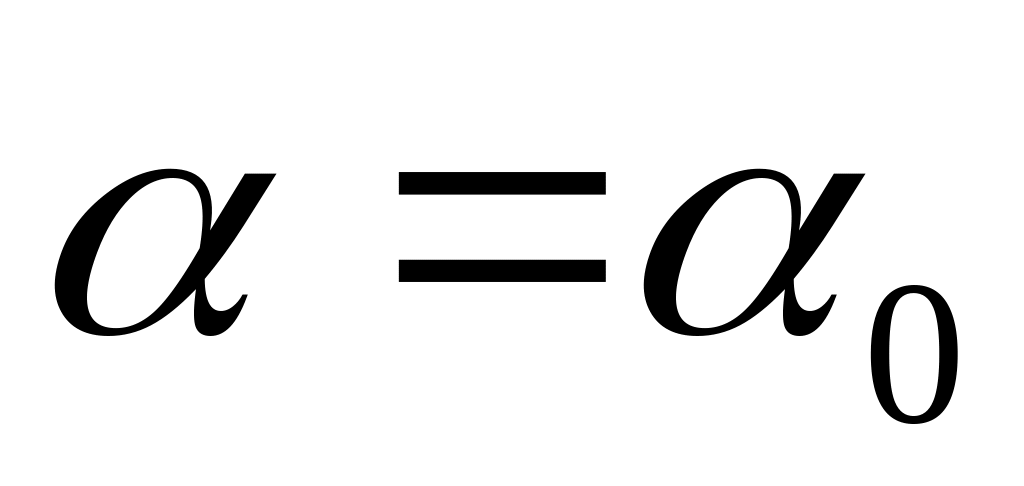
	Знаходження розв’язання задачі Коші
	Знаходження розв’язання задачі Коші
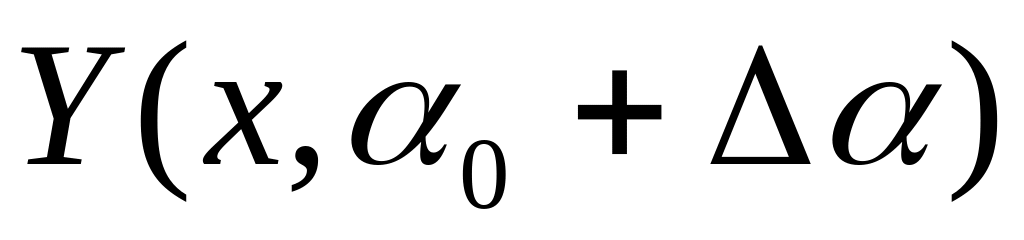
	до
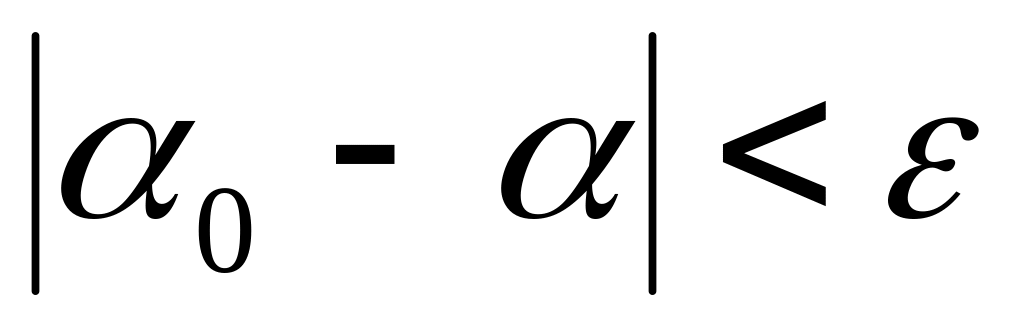
Вивід

Рисунок - 2 – Алгоритм методу стрілянини

Наприклад, розглянемо систему двох рівнянь першого порядку

(12)

Граничні умови задані у вигляді

(13)

Процес розв’язання цієї граничної задачі методом стрілянини полягає в наступному. Вибирається деяке що є початковим наближенням для . Вирішується задачі Коші для системи (12) з початковими умовами . В результаті розв’язання при х = 1 виходить деяке значення . Якщо різниця між цими величинами невелика, то знайдене розв’язання задачі Коші береться за шукане розв’язання граничної задачі. Інакше знаходиться уточнене значення і процес повторюється.

Таким чином, метод стрілянини може бути також використаний як для розв’язання граничних завдань для рівнянь вищих порядків, так і для систем рівнянь.