М ИНОБРНАУКИ РОССИИ

ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ

УЧРЕЖДЕНИЕ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ

«САМАРСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ»

(ФГБОУ ВПО «САМГТУ»)

Ю.А. Тычинина

СТРУКТУРЫ И АЛГОРИТМЫ

ОБРАБОТКИ ДАННЫХ:

РЕАЛИЗАЦИЯ НА ЯЗЫКЕ

ВЫСОКОГО УРОВНЯ С++

Лабораторный практикум

Самара

Самарский государственный технический университет

2014

УДК

Т 93

Р е ц е н з е н т ы: канд. техн. наук А.А. Афиногентов,

Тычинина Ю.А.

Т 93 Структуры и алгоритмы обработки данных: реализация на языках высокого уровня: лабораторный практикум. / Ю.А. Тычинина. – Самара. Самар.гос.техн.ун-т, 2014. – 261 с.: ил.

ISBN

Приведены основные понятия алгоритмизации, свойства алгоритмов, общие принципы их построения, основные алгоритмические конструкции. На примерах рассматриваются средства языка С++, используемые в рамках структурной парадигмы программирования: стандартные типы данных, основные конструкции, массивы, строки, структуры, функции и т.д. По всем рассматриваемым темам представлены контрольные задания в 10 вариантах.

Изложенные в настоящем практикуме материалы найдут применение при изучении дисциплины «Структуры и алгоритмы обработки данных».

Лабораторный практикум предназначен для студентов высших технических учебных заведений, обучающихся по направлению подготовки 220400 «Управление в технических системах» и смежным направлениям.

УДК

Т 93

ISBN  Ю.А. Тычинина, 2014

 Самарский государственный

технический университет, 2014

Введение

Современная методология программирования предполагает, что такие аспекты программирования, как запись алгоритма на языке программирования и выбор структур представления данных, заслуживают большого внимания. Всем, кто занят вопросами программирования для вычислительной техники, известно, что решение о том, как представлять данные, невозможно принимать без понимания того, какие алгоритмы будут к ним применяться, и наоборот, выбор алгоритма часто очень сильно зависит от строения данных, к которым он применяется.

Без знания структур данных и алгоритмов невозможно создать серьезный программный продукт. В связи с этим цель данного практикума – помочь студенту освоить структурное программирование на языке С++. В основе лабораторного практикума лежит практический подход, и все важные положения демонстрируются большим количеством примеров. Лабораторный практикум предназначен для изучения структурного программирования на лабораторных работах и практических занятиях по предмету «Структуры и алгоритмы обработки данных» для студентов, обучающихся по направлению «Управление в технических системах» и смежным направлениям.

Анализ сложности алгоритма [2, 8]

Сложность алгоритма — это способ формально измерить, насколько быстро программа или алгоритм работают.

Существует ряд важных причин для анализа алгоритмов. Одной из них является необходимость получения оценок или границ для объема памяти или времени работы, которое потребуется алгоритму для успешной обработки конкретных данных. Для оценки качества алгоритма вводится понятие сложность алгоритма, или обратное понятие — эффективность алгоритма. Чем большее время и объем памяти требуются для реализации алгоритма, тем больше его сложность и соответственно ниже эффективность. Сложность алгоритма делится на временную и емкостную.

Временная сложность — это критерий, характеризующий временные затраты на реализацию алгоритма. Емкостная сложность — критерий, характеризующий затраты памяти на те же цели. В зависимости от конкретной формы этих критериев сложность алгоритма в свою очередь подразделяется на практическую и теоретическую. Практическая временная сложность обычно оценивается во временных единицах (секунды, миллисекунды, количество временных тактов процессора, количество выполнения циклов и т.п.). Практическая емкостная сложность выражается, как правило, в битах, байтах, словах и т.п.

Основные факторы, от которых может зависеть сложность алгоритма:

• быстродействие компьютера и его емкостные ресурсы (в первую очередь — объем оперативной памяти). Чем ниже тактовая частота процессора и меньше объем оперативного запоминающего устройства, тем медленнее выполняются арифметические и логические операции, тем чаще (для больших задач) приходится обращаться к медленно действующей внешней памяти, и, следовательно, больше времени уходит на реализацию алгоритма;

• выбранный язык программирования. Задача, запрограммированная, например, на языке Ассемблера, в общем случае решится быстрее, чем по тому же самому алгоритму, но запрограммированному на языке более высокого уровня, например на Паскале;

• выбранный математический метод формулирования задачи;

• искусство и опыт программиста. В общем случае по одному и тому же алгоритму опытный программист напишет более эффективно работающую программу, чем его начинающий коллега.

Какой алгоритм выбрать для решения конкретной задачи? Этот вопрос очень тщательно прорабатывается в программировании.

Эффективность программы является очень важной характеристикой, которая состоит из двух составляющих: память (или пространство) и время. Пространственная эффективность измеряется количеством памяти, требуемой для выполнения программы.

Компьютеры обладают ограниченным объемом памяти. Если две программы реализуют идентичные функции, то та, которая использует меньший объем памяти, характеризуется большей пространственной эффективностью. Иногда память становится доминирующим фактором в оценке эффективности программ. Однако в последние годы в связи с быстрым ее удешевлением эта составляющая эффективности постепенно теряет свое значение. Временная эффективность программы определяется временем, необходимым для ее выполнения.

Лучший способ сравнения эффективностей алгоритмов состоит в сопоставлении их порядков сложности. Этот метод применим как к временной, так и пространственной сложности. Порядок сложности алгоритма выражает его эффективность обычно через количество обрабатываемых данных. Например, некоторый алгоритм может существенно зависеть от размера обрабатываемого массива. Если, например, время обработки удваивается с удвоением размера массива, то порядок временной сложности алгоритма определяется как размер массива. Порядок алгоритма — это функция, доминирующая над точным выражением временной сложности.

Сложность алгоритма — это то, что основывается на сравнении двух алгоритмов на идеальном уровне, игнорируя низкоуровневые детали вроде реализации языка программирования, «железа», на котором запущена программа, или набора команд в данном центральном процессоре. Необходимо сравнивать алгоритмы с точки зрения идеи: как происходит вычисление. Подсчёт миллисекунд тут мало поможет. Вполне может оказаться, что плохой алгоритм, написанный на низкоуровневом языке (например, ассемблере) будет намного быстрее, чем хороший алгоритм, написанный языке программирования высокого уровня (например, С++).

Алгоритм — это программа, которая является исключительно вычислением, без других часто выполняемых компьютером вещей — сетевых задач или пользовательского ввода-вывода. Анализ сложности позволяет узнать, насколько быстро работает эта программа в процессе вычисления. Примерами чисто вычислительных операций могут послужить операции над числами с плавающей точкой (сложение и умножение), поиск заданного значения в находящейся в ОЗУ базе данных или запуск шаблона регулярного выражения на соответствие строке. Очевидно, что вычисления встречаются в компьютерных программах повсеместно. 

Анализ сложности также позволяет объяснить, как будет вести себя алгоритм при возрастании входного потока данных. Если алгоритм выполняется одну секунду при 1000 элементах на входе, то как он себя поведёт, если мы удвоим это значение? Будет работать также быстро, в полтора раза быстрее или в четыре раза медленнее? В практике программирования такие предсказания крайне важны. Например, если создан алгоритм для web-приложения, работающего с тысячей пользователей, и измерено его время выполнения, то используя анализ сложности, можно получить представление о том, что случится, когда число пользователей возрастёт до двух тысяч.

Способы оценки сложности алгоритмов

Подсчёт инструкций

Дан входной массив А размера n.: int Max= A[ 0 ];

for (int i=0; i<n; ++i) {

if (A[i]>=Max) {

Max=A[i];

}

}

Сначала подсчитаем, сколько здесь вычисляется фундаментальных инструкций. В процессе анализа данного кода, имеет смысл разбить его на простые инструкции — задания, которые могут быть выполнены процессором мгновенно или близко к этому. Предположим, что процессор способен выполнять как единые инструкции следующие операции:

• присваивать значение переменной;

• находить значение конкретного элемента в массиве;

• сравнивать два значения;

• инкрементировать значение;

• основные арифметические операции (например, сложение и умножение).

Предположим, что ветвление (выбор между if и else частями кода после вычисления if-условия) происходит мгновенно, и не будем учитывать эту инструкцию при подсчёте. Для первой строки в коде выше:

int Max=A[0];

требуются две инструкции: для поиска A[0] и для присвоения значения Max (мы предполагаем, что n всегда как минимум 1). Эти две инструкции будут требоваться алгоритму, вне зависимости от величины n. Инициализация цикла for тоже будет происходить постоянно, что даёт нам ещё две команды: присвоение и сравнение.

i = 0;

i < n;

Всё это происходит до первого запуска for. После каждой новой итерации мы будем иметь на две инструкции больше: инкремент i и сравнение для проверки, не пора ли нам останавливать цикл.

++i;

i < n;

Таким образом, если проигнорировать содержимое тела цикла, то количество инструкций у этого алгоритма 4 + 2n — четыре на начало цикла for и по две на каждую итерацию, которых мы имеем n штук. Теперь можно определить математическую функцию f(n) такую, что зная n, можно определить и необходимое алгоритму количество инструкций. Для цикла for с пустым телом f(n) = 4 + 2n. 

Анализ наиболее неблагоприятного случая

В теле цикла имеем операции поиска в массиве и сравнения, которые происходят всегда:

if (A[i]>=Max) { ...

Но тело if может запускаться, а может и нет, в зависимости от актуального значения из массива. Если произойдёт так, что A[i]>=M, то запустятся две дополнительные команды: поиск в массиве и присваивание:

Max =A[ i ]

В этом случае уже не возможно также легко определить f(n), потому что теперь количество инструкций зависит не только от n, но и от конкретных входных значений. Например, для A=[1,2,3,4] программе потребуется больше команд, чем для A=[4,3,2,1]. При анализе алгоритмов, чаще всего рассматривается наихудший сценарий. Каким он будет в данном случае? Когда алгоритму потребуется больше всего инструкций до завершения? Ответ: когда массив упорядочен по возрастанию, как, например, A=[1,2,3,4]. Тогда Max будет переприсваиваться каждый раз, что даст наибольшее количество команд. Теоретики имеют для этого причудливое название — анализ наиболее неблагоприятного случая, который является ни чем иным, как просто рассмотрением максимально неудачного варианта. Таким образом, в наихудшем случае в теле цикла из рассматриваемого кода запускается четыре инструкции, и получается f(n)=4+2n+4n=6n+4.  (Дополнительные 4 команды: поиск очередного элемента, сравнение, выбор ветки вычислений и присваивание, причем 2 из них будут не во всех итерациях).

Асимптотическое поведение

С полученной выше функцией имеем весьма хорошее представление о том, насколько быстр алгоритм. Количество инструкций у конкретного процессора, необходимое для реализации каждого положения из используемого языка программирования, зависит от компилятора этого языка и доступного процессору (AMD или Intel Pentium на персональном компьютере, MIPS на Playstation 2 и т.п. ) набора команд. Для получения объективной оценки сложности алгоритма необходимо игнорировать условия такого рода, поэтому пропустим функцию f через «фильтр» для очищения её от незначительных деталей, на которые теоретики предпочитают не обращать внимания.

Тогда функция 6n+4 состоит из двух элементов: 6n и 4. При анализе сложности важность имеет только то, что происходит с функцией подсчёта инструкций при значительном возрастании n. Это совпадает с предыдущей идеей «наихудшего сценария»: интерес представляет поведение алгоритма, находящегося в «плохих условиях», когда он вынужден выполнять что-то трудное. Именно это по-настоящему полезно при сравнении алгоритмов. Если один из них работает лучше другого при большом входном потоке данных, то велика вероятность, что он останется быстрее и на лёгких, маленьких потоках. Поэтому отбрасываем те элементы функции, которые при росте n возрастают медленно, и оставляем только те, что растут сильно. Очевидно, что 4 останется 4 вне зависимости от значения n, а 6n, наоборот, будет расти. Поэтому первое, что мы сделаем, — это отбросим 4 и оставим только f(n)=6n.

Имеет смысл думать о 4 просто как о «константе инициализации». Разным языкам программирования для настройки может потребоваться разное время. Например, Java сначала необходимо инициализировать свою виртуальную машину. Для нивелирования факта различия языков программирования, отбросим это значение.

Второй вещью, на которую можно не обращать внимания, является множитель перед n. Так что наша функция превращается в f(n)=n и этот факт многое упрощает. Константный множитель имеет смысл отбрасывать, если думать о различиях во времени компиляции разных языков программирования. «Поиск в массиве» для одного языка программирования может компилироваться совершенно иначе, чем для другого.

Различные языки программирования будут подвержены влиянию различных факторов, которые отразятся на подсчёте инструкций. Пренебрежение этим фактором идёт в русле игнорирования различий между конкретными языками программирования с сосредоточением на анализе самой идеи алгоритма как таковой.

Описанные выше фильтры — «отбрось все факторы» и «оставляй только наибольший элемент» — в совокупности дают то, что называется асимптотическим поведением. Для f(n)=2n+8 оно будет описываться функцией f(n)=n.

Найдём асимптотики для следующих примеров, используя принципы отбрасывания константных факторов и оставления только максимально быстро растущего элемента:

1. f(n)=5n+12 даст f(n)=n. 

Основания — те же, что были описаны выше

2. f(n)=109 даст f(n)=1.

Мы отбрасываем множитель в 109·1, но 1 по-прежнему нужен, чтобы показать, что функция не равна нулю

3. f(n) = n² + 3n + 112 даст f(n)=n².

Здесь n² возрастает быстрее, чем 3n, который, в свою очередь, растёт быстрее 112

4. f(n)=n³ + 1999n + 1337 даст f(n)=n³.

Несмотря на большую величину множителя перед n, мы по прежнему полагаем, что можем найти ещё больший n, поэтому f(n) = n³ всё ещё больше 1999n. 

5. f(n) = n + sqrt( n ) даст f( n ) = n. 

Потому что n при увеличении аргумента растёт быстрее, чем sqrt(n).

Сложность

Из предыдущей части можно сделать вывод, что если отбросить все константы, то говорить об асимптотике функции подсчёта инструкций программы будет очень просто. Фактически, любая программа, не содержащая циклы, имеет f(n)=1, потому что в этом случае требуется константное число инструкций (при отсутствии рекурсии). Одиночный цикл от 1 до n, даёт асимптотику f(n)=n, поскольку до и после цикла выполняет неизменное число команд, а постоянное же количество инструкций внутри цикла выполняется n раз.

Руководствоваться подобными соображениями рассмотрим несколько примеров. Следующая программа проверяет, содержится ли в массиве A размера n заданное значение:

exists = false;

for (int i = 0; i < n; i++ ) {

if (int A[i]==value) {

exists = true;

break;

}

}

Такой метод поиска значения внутри массива называется линейным поиском. Это обоснованное название, поскольку программа имеет f(n)=n. Инструкция break позволяет программе завершиться раньше, даже после единственной итерации. Однако, интерес представляет самый неблагоприятный сценарий, при котором массив A вообще не содержит заданное значение. Поэтому f(n) = n по-прежнему.

Теперь рассмотрим программу, которая складывает два значения из массива и записывает результат в новую переменную:

v=a[0]+a[1]

Здесь постоянное количество инструкций, следовательно, f(n)=1.

Следующая программа на C++ проверяет, содержит ли вектор (своеобразный массив) A размера n два одинаковых значения:

bool duplicate = false;

for ( int i = 0; i < n; i++ ) {

for ( int j = 0; j < n; j++ ) {

if ( i!=j && A[ i ]==A[ j ] ) {

duplicate = true;

break;

}

}

if ( duplicate ) {

break;

}

}

Два вложенных цикла дадут асимптотику вида f(n)= n².

Таким образом, простые программы можно анализировать с помощью подсчёта в них количества вложенных циклов. Одиночный цикл в n итераций даёт f(n)=n. Цикл внутри цикла — f( n ) = n². Цикл внутри цикла внутри цикла — f(n) = n³. И так далее.

Если в программе в теле цикла вызывается функция, и известно число выполняемых в ней инструкций, то легко определить общее количество команд для программы целиком.

Рассмотрим в качестве примера следующий код:

int i;

for ( i = 0; i < n; ++i ) {

f( n );

}

Если известно, что f(n) выполняет ровно n команд, то мы можем сказать, что количество инструкций во всей программе асимптотически приближается к n², поскольку f(n) вызывается n раз.

Таким образом, если имеется серия из последовательных for-циклов, то асимптотическое поведение программы определяет наиболее медленный из них. Два вложенных цикла, идущие за одиночным, асимптотически тоже самое, что и вложенные циклы в сами по себе. Говорят, что вложенные циклы доминируют над одиночными. 

Рассмотрим систему обозначений, используемую теоретиками. Когда необходимо выяснить точную асимптотику f, мы говорим, что программа — Θ(f(n)). Θ(n) произносится как «тета от n». Иногда говорят, что f(n) (оригинальная функция подсчёта инструкций, включая константы) есть Θ(x). Например, можно сказать, что f(n)=2n — это функция, являющаяся Θ(n). Можно так же написать, что 2n∈Θ(n), что произносится: «два n принадлежит тета от n». Nакая нотация говорит о том, что если подсчитать количество необходимых программе команд, и оно будет равно 2n, то асимптотика этого алгоритма описывается как n (что находят, отбрасывая константу). Примеры:

1. n⁶ + 3n ∈ Θ( n⁶);

2. 2ⁿ + 12 ∈ Θ( 2ⁿ );

3. 3ⁿ + 2ⁿ ∈ Θ( 3ⁿ );

4. nⁿ + n ∈ Θ( nⁿ ).

Функция Θ(х) – временная сложность, или просто сложность алгоритма. Таким образом, алгоритм с Θ(n) имеет сложность n. Также существуют специальные названия для Θ(1), Θ(n), Θ(n²) и Θ(log(n)), потому что они встречаются очень часто. Говорят, что Θ(1) — алгоритм с константным временем, Θ(n) — линейный, Θ(n²) — квадратичный, а Θ(log(n)) — логарифмический.

Нотация «большое О»

В реальной жизни иногда проблематично выяснить точно поведение алгоритма тем способом, который рассматривался выше. Особенно для более сложных примеров. Однако, можно сказать, что поведение алгоритма никогда не пересечёт некой границы. Это делает жизнь проще, так как чёткого указания на то, насколько быстр алгоритм, может и не появиться, даже при условии игнорирования констант (как раньше). Всё, что нужно — найти эту границу.

Наиболее известной задачей, которую используют при обучении алгоритмам, является сортировка. Даётся массив A размера n и необходимо написать программу, его сортирующую. Интерес тут в том что, такая необходимость часто возникает в реальных системах. Например, обозревателю файлов нужно отсортировать файлы по имени, чтобы облегчить пользователю навигацию по ним. Или другой пример: в видео игре может возникнуть проблема сортировки 3D объектов, демонстрируемых на экране, по их расстоянию от точки зрения игрока в виртуальном мире, чтобы определить, какие из них будут для него видимы, а какие — нет (Visibility Problem). Сортировка также интересна тем, что для неё существует множество алгоритмов, одни из которых хуже, чем другие.

Рассмотрим метод сортировки выбором:

• находится минимальный элемент массива, который помещается в новый массива и удаляется из оригинального;

• среди оставшихся значений снова находится минимум, добавляется в новый массив (который теперь содержит два значения) и удаляется из старого;

• процесс повторяется, пока все элементы не будут перенесены из первоначального в новый массив, что будет означать конец сортировки.

При реализации данного метода сортировки массива A[n] имеем два вложенных цикла. Внешний цикл выполняется n раз, а внутренний — по разу для каждого элемента массива А. Поскольку изначально A имеет n элементов и на каждой итерации удаляется один из них, то сначала внутренний цикл выполняется n раз, потом n-1, n-2 и так далее, пока на последней итерации внутренний цикл не пройдёт всего один раз.

Если рассматривать сумму 1+2+...+(n-1)+n, то найти сложность этого алгоритма будет несколько проблематично. Но можно найти для неё «верхний предел». Для этого нужно изменить программу (можно мысленно, не трогая код), чтобы сделать её хуже, чем она есть, а затем вывести сложность для того, что получилось. Тогда можно будет уверенно сказать, что оригинальная программа работает или также плохо, или (скорее всего) лучше.

Теперь можно подумать над тем, как ухудшить программу, чтобы упростить для неё вывод сложности, например, добавляя в код новые инструкции, чтобы оценка имела смысл для оригинальной программы. Очевидно, что можно изменить внутренний цикл программы, заставив его вычисляться n раз на каждой итерации. Некоторые из этих повторений буду бесполезны, но зато это поможет проанализировать сложность результирующего алгоритма. Если внести это небольшое изменение, то новый алгоритм будет иметь Θ(n²), поскольку получится два вложенных цикла, каждый из которых выполняется ровно n раз. А если это так, то оригинальный алгоритм имеет O(n²). O(n²) произносится как «большое О от n в квадрате». Это говорит о том, что программа асимптотически не хуже, чем n². Она будет работать или лучше, или также. Если код действительно имеет Θ(n²), то можно сказать также, что он O(n²). Таким образом, Θ(n²) для программы — это и O(n²) тоже. Обратное верно не всегда.

Итак, если анализ показал, что программа имеет O(n²), то программа никогда не будет работать хуже, чем n². Это даёт хорошую оценку того, насколько быстра программа.

Виды функции сложности алгоритмов

Функция сложности 0(1). В алгоритмах константной сложности большинство операций в программе выполняется один или несколько раз. Любой алгоритм, всегда требующий независимо от размера данных одного и того же времени, имеет константную сложность.

Функция сложности 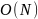. Время работы программы линейно, обычно, когда каждый элемент входных данных требуется обработать лишь линейное число раз.

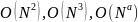Функция сложности — полиномиальная функция сложности.

Функция сложности 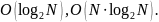Такое время работы имеют те алгоритмы, которые делят большую проблему на множество небольших, а затем, решив их, объединяют решения.

Функция сложности . Экспоненциальная сложность. Такие алгоритмы чаще всего возникают в результате подхода, именуемого «метод грубой силы».

Нотация «большое Ω»

Выше для анализа программа искусственно менялась в худшую сторону для получения O. Такая оценка говорит о том, что код никогда не будет работать медленнее определённого предела. Из этого можно получить основания для оценки: достаточно ли хороша программа? Если поступить противоположным образом, сделав имеющийся код лучше, и найти сложность того, что получится, то задействуется Ω-нотацию. Таким образом, Ω даёт сложность, лучше которой программа быть не может. Она полезна, если нужно доказать, что программа работает медленно или алгоритм является плохим. Так же её можно применить, когда утверждается, что алгоритм слишком медленный для использования в данном конкретном случае. Например, высказывание, что алгоритм является Ω(n³), означает, что алгоритм не лучше, чем n³. Он может быть Θ(n³), или Θ(n⁴), или ещё хуже, но мы будем знать предел его быстродействия. Таким образом, Ω даёт нижнюю границу сложности алгоритма. Если верхняя и нижняя границы сложности нестрогие, то можно писать соответственно o и ω вместо O и Ω. Например, Θ(n³) алгоритм является ο(n⁴) и ω(n²). Ω(n) произносится как «большое омега от n», в то время как ω(n) произносится «маленькое омега от n».

Рекурсивная сложность

Рекурсивная функция — это функция, которая вызывает сама себя. Каким образом можно проанализировать её сложность? Следующая функция вычисляет факториал заданного числа. Факториал целого положительного числа находится как произведение всех предыдущих положительных целых чисел. Например, факториал 5 — это 5 · 4 · 3 · 2 · 1.

int factorial( n );

if n == 1:

return 1

return n*factorial( n - 1 );

Проанализируем эту функцию. Она не содержит циклов, но её сложность всё равно не является константной. Придётся вновь заняться подсчётом инструкций. Очевидно, что если применить эту функцию к некоторому n, то она будет вычисляться n раз. Таким образом, эта функция является Θ(n).

Логарифмическая сложность

Одной из известнейших задач в информатике является поиск значения в массиве. Если есть отсортированный массив, в котором необходимо найти заданное значение. Одним из способов сделать это является бинарный поиск:

• выбирается средний элемент из массива:

• если он совпадает с тем, что искали, то задача решена.

• в противном случае, если заданное значение больше этого элемента, то оно должно лежать в правой части массива А, если меньше — то в левой.

• будем разбивать эти подмассивы до тех пор, пока не получим искомое. 

Первая итерация цикла имеет дело со всем списком. Каждая последующая итерация делит пополам размер массива. Так, размерами списка для алгоритма являются

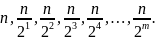
В конце концов будет такое целое m, что 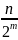< 2 или n < . Так как m — это первое целое, для которого < 2, то должно быть верно 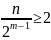или 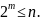Из этого следует, что 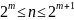. Возьмем логарифм каждой части неравенства и получим 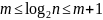. Отсюда .

Последний результат позволяет сравнивать бинарный поиск с линейным. Несомненно, log(n) намного меньше n, из чего правомерно заключить, что первый намного быстрее второго. Так что имеет смысл хранить массивы в отсортированном виде, если планируется часто искать в них значения.

Контрольные вопросы

1. Для чего нужна оценка сложности алгоритма?

2. Что означает утверждение «сложность алгоритма θ(n)»?

3. Что означает утверждение «сложность алгоритма O(n)»?

4. Что означает утверждение «сложность алгоритма Ω(n)»?

5. Что означает утверждение «сложность алгоритма ω(n)»?

6. Что означает утверждение «сложность алгоритма o(n)»?