Министерство образования и науки Российской Федерации

Федеральное государственное автономное образовательное учреждение

высшего профессионального образования

«Волгоградский государственный университет»

Институт приоритетных технологий

Кафедра судебной экспертизы и физического материаловедения

Лабораторная работа № 9

КРУТИЛЬНЫЙ МАЯТНИК

Методические указания

Волгоград,2014

Лабораторная работа № 9

КРУТИЛЬНЫЙ МАЯТНИК

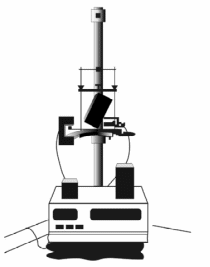
1. Цель работы: изучение крутильных колебаний и определение методом крутильных колебаний моментов инерции твердых тел.

2. Оборудование: лабораторная установка.

3. Материал для изучения:

Крутильные колебания.

Момент инерции твердого тела.

Зависимость момента инерции твердого тела от положения оси

вращения.

4. Теоретическое введение

В работе проверяется соотношение

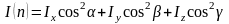(1)

для однородных симметричных твердых тел (куб, прямоугольный параллелепипед). Главные оси таких тел являются осями симметрии. Они перпендикулярны граням и проходят через геометрический центр тела (рис. 1).

Рис.1

Для измерения моментов инерции твердого тела относительно оси. определяемой единичным вектором

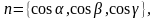
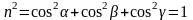(2)

где α, β и 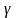— углы между направлениями вектора n и осями координат OX, OY и OZ (рис. 2), применяется метод крутильных колебаний.

Рис.2

Исследуемое твердое тело жестко закрепляется в рамке крутильного маятника, подвешенной на упругой вертикально натянутой проволоке. Если вывести маятник из положения равновесия, то он будет совершать колебания. Период этих колебаний равен

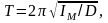(3)

где I_M — момент инерции маятника относительно оси вращения, D—постоянная момента упругих сил (см. раздел 3).

Момент инерции маятника равен сумме момента инерции I₀ рамки и моментов инерции I исследуемого тела:

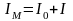
Поэтому период колебаний маятника

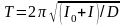(4)

Если колеблется свободная рамка без тела, то ее период колеба­ний, очевидно, равен

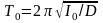(5)

Из этих уравнений можно исключить неизвестную величину D. В результате находим

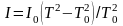(6)

Соотношение (6) позволяет выразить момент инерции I тела относительно оси маятника через момент инерции I₀ свободной рамки. Для этого нужно измерить периоды колебаний То и Т соответственно для свободной рамки и для рамки с телом. Период колебаний Т, так же как и момент инерции I тела, зависит от ориентации тела по отношению к оси маятника. Запишем (6) в виде:

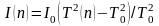(7)

где n — единичный вектор, направленный вдоль оси маятника. В лабораторной установке ось маятника (она же ось вращения тела) направлена по вертикали. Поэтому во всех опытах следует считать, что единичный вектор n направлен вертикально вверх. Момент инерции тела относительно вертикальной оси, т. е. I (n), изменяют, поворачивая тело и закрепляя его в различных положениях по отношению к этой оси (рис. 3).

Рис.3

Направив оси OX, OY и OZ вдоль главных осей тела, мы выбрали систему координат OXYZ, жестко связанную с телом. Поворачивая тело, мы изменяем направления вектора n в жестко связанной с телом системе координат OXYZ. Закрепим тело в рамке так, чтобы ось вращения n совпадала с какой-либо его главной осью OX, OY или OZ. Тогда из (7) получим

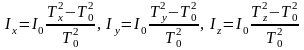(8)

где Тх, Ту и Тz — соответственно периоды колебаний маятника, когда ось его вращения n совпадает с одной из главных осей ОХ, OY или OZ.

Подставив (7) и (8) в исходное соотношение (1), получим

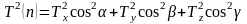(9)

Таким образом, существует простая связь между периодами кру­тильных колебаний тела Т_x Т_y и Т_z, относительно его осей симметрии OX, OY и OZ и периодом колебаний этого же тела относительно оси n с направляющими косинусами cos α, cos β и cos .

Выражение (9), так же как и формула (3) для периода крутильных колебаний, справедливо, если затухание мало. Практически для этого достаточно, чтобы число колебаний N, за которое амплитуда уменьшается в 2—3 раза, удовлетворяло неравенству N ≥ 10 (подробнее см. описание работы 6). Если это неравенство выполняется, то проверка соотношения (1) сводится к проверке равенства (9). Оно удобно тем, что все входящие в него величины в условиях опыта могут быть измерены непосредственно.