
- •Первообразная. Неопределенный интеграл и его свойства.
- •Упражнения
- •Метод замены переменной (метод подстановки)
- •Упражнения
- •Метод интегрирования по частям
- •Упражнения
- •Интегрирование рациональных функций.
- •Интегрирование иррациональных и трансцендентных функций.
- •Интегрирование основных классов элементарных функций
- •Интегрирование дробно-рациональных функций
- •1. , Целое) . 3.
- •Решив эту систему, найдем коффициенты
- •Упражнения.
- •Интегрирование выражений, содержащих тригонометрические функции
- •2) Интегралы вида
- •3) Интегралы вида
- •Упражнения
- •Упражнения
- •Смешанные задачи на интегрирование
- •Проведя в точках деления [a,b] прямые, параллельные оси ординат, разобьем криволинейную трапецию на n частичных трапеций. В каждом частичном интервале возьмем точки x1,x2,…,xт, так что
- •Оценка интеграла. Теорема о среднем. Формула Ньютона-Лейбница. Замена переменных и интегрирование по частям в определенном интеграле.
- •Приложения определенного интеграла.
- •Несобственные интегралы
- •Несобственные интегралы от неограниченных функций
- •1 Вычисление площадей плоских фигур
- •Упражнения
- •Вычисление длин дуг плоских кривых
- •Вычисление объемов тел вращения
- •Упражнения
Метод интегрирования по частям
Формулой интегрирования по частям в неопределенном интеграле называется формула
![]()
где u=u(x)
и v=v(x)
дифференцируемые
функции от х.
Она позволяет свести нахождение интеграла
![]() к нахождению интеграла
к нахождению интеграла
![]()
Большую часть интегралов, при нахождении которых применяется формула интегрирования по частям, можно разбить на три группы.
Интегралы вида
![]()
где Р(х)
многочлен некоторой степени n.
За функцию u(x)
следует
взять одну из функций
![]()
![]() ,
тогда
,
тогда
![]() .
.
Интегралы вида
![]() ,
,
где Р(х)
многочлен, а k
– некоторое число. Для их нахождения
следует положить u=P(x),
а
![]() соответственно.
соответственно.
Интегралы вида
![]()
где a и b – некоторые числа. Эти интегралы находятся с помощью двукратного интегрирования по частям.
Пример. Найти
интеграл
![]() Решение. Применим формулу интегрирования
по частям. За функцию u(x)
возьмем
Решение. Применим формулу интегрирования
по частям. За функцию u(x)
возьмем
![]() ,
тогда
,
тогда
![]() .
Будем иметь
.
Будем иметь

Пример. Найти
интеграл
![]()
Решение.
![]()
Полученный интеграл снова находим интегрированием по частям.
![]()
Подставляя значение полученного интеграла в предыдущее выражение, будем иметь
![]()
Перенося искомый интеграл из правой части равенства в левую, получаем
![]()
Окончательно имеем
![]() .
.
Упражнения
1.
![]() .
2.
.
2.
![]()
3.
![]() 4.
4.
![]()
5.
![]() 6.
6.
![]()
7.![]() 8.
8.
![]()
9.
![]() 10.
10.
![]()
11.
![]() 12.
12.
![]()
13.
![]() .
14.
.
14.
![]() .
.
15.
![]() 16.
16.
![]()
17.
![]() .
18.
.
18.
![]()
19.
![]() 20.
20.
![]()
НЕДЕЛЯ 10
Лекция 19-20
Интегрирование рациональных функций.
Важный класс функций, интегралы от которых всегда выражаются через элементарные функции, образуют рациональные функции, то есть функции, которые можно представить в виде дроби
![]()
где P(x), Q(x) – многочлены.
Если степень многочлена в числителе равна или больше степени многочлена в знаменателе, то, выполнив деление, получим
![]()
где W(x) – некоторый многочлен, а R(x) – многочлен степени ниже, чем Q(x).
Пример.
![]()
Многочлен W(x) представляет собой линейную комбинацию целых неотрицательных степеней x и поэтому может быть проинтегрирован. Теперь рассмотрим вопрос интегрирования правильной дроби из последнего соотношения.
Знаменатель
правильной дроби разлагается на множители
вида
![]() и
и
![]() а дробь разлагается на сумму элементарных
дробей следующим образом
а дробь разлагается на сумму элементарных
дробей следующим образом

Интегралы данных дробей приводятся к интегралам следующего вида


![]()
Интеграл
![]() вычисляется по рекуррентной формуле
вычисляется по рекуррентной формуле
![]()

Таким образом, можно сделать вывод о том, что всякая рациональная функция может быть проинтегрирована в элементарных функциях.
Интегрирование иррациональных и трансцендентных функций.
Предварительно введем понятие рациональной функции от двух переменных u и v, то есть функции получающейся из этих переменных и некоторых постоянных, над которыми производятся только операции сложения, вычитания, умножения и деления R(u, v). Такова, например, функция
![]()
Если переменные
u
и v,
в свою очередь являются функциями
переменной x:
![]() то функция
то функция
![]() называется рациональной функцией от
называется рациональной функцией от
![]() и
и
![]()
Рассмотрим теперь интегралы от некоторых простейших иррациональных и трансцендентных функций сводящихся к интегралам от рациональных функций.
Интегралы вида
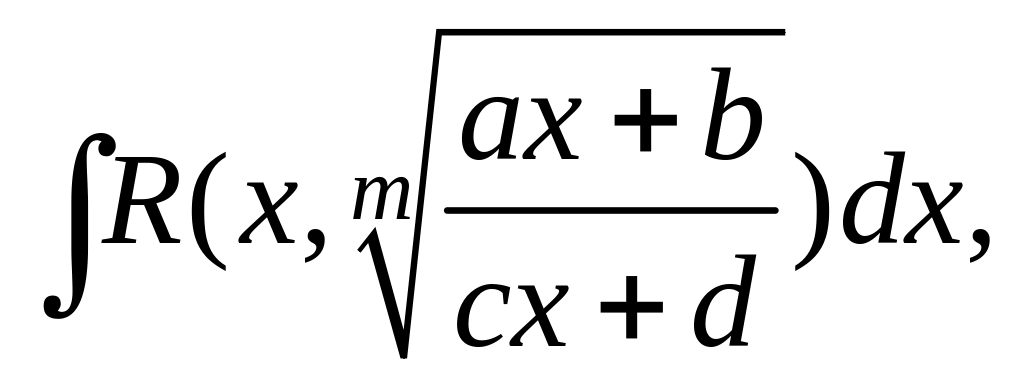 где a,
b,
c,
d
– некоторые
числа
где a,
b,
c,
d
– некоторые
числа
 m
– натуральное число. Интегралы данного
вида рационализируются подстановкой
m
– натуральное число. Интегралы данного
вида рационализируются подстановкой

Интеграл вида
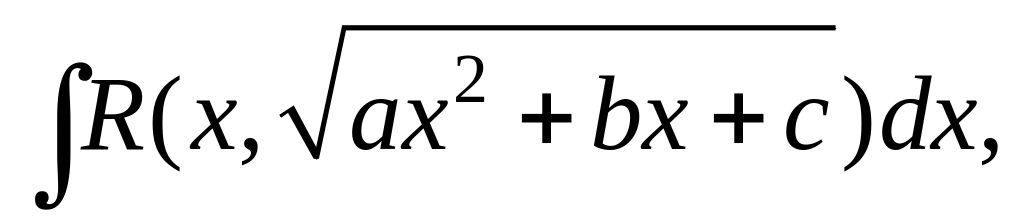 где a,
b,
c
– некоторые
числа
где a,
b,
c
– некоторые
числа
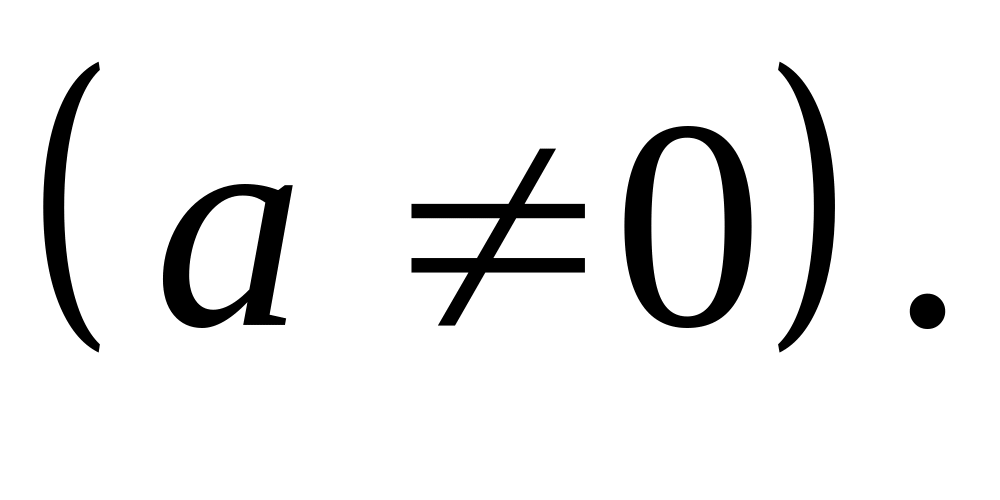 Данный интеграл зависит от корней
квадратного трехчлена
Данный интеграл зависит от корней
квадратного трехчлена
 Если этот трехчлен имеет два различных
действительных корня x1
и x2,
то он сводится к интегралу вида 1, а
именно к интегралу
Если этот трехчлен имеет два различных
действительных корня x1
и x2,
то он сводится к интегралу вида 1, а
именно к интегралу

Если x1=x2, то интеграл сводится к интегралу от рациональной функции, а именно к интегралу
![]()
Если же квадратный трехчлен не имеет вещественных корней, то с помощью подстановки Эйлера
![]()
данный интеграл приводится к интегралу от рациональной функции
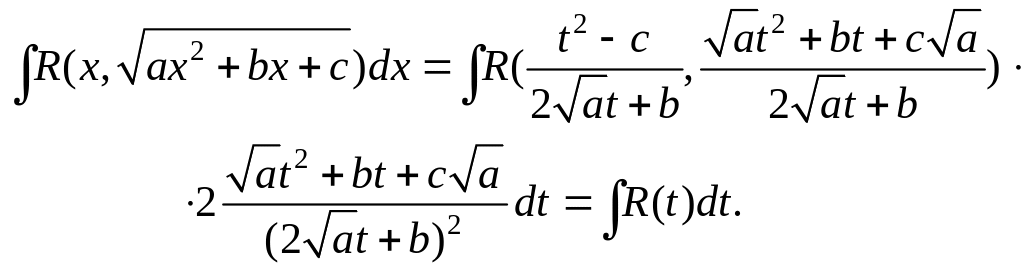
Интеграл вида
 рационализируется
подстановкой
рационализируется
подстановкой
 Действительно,
Действительно,
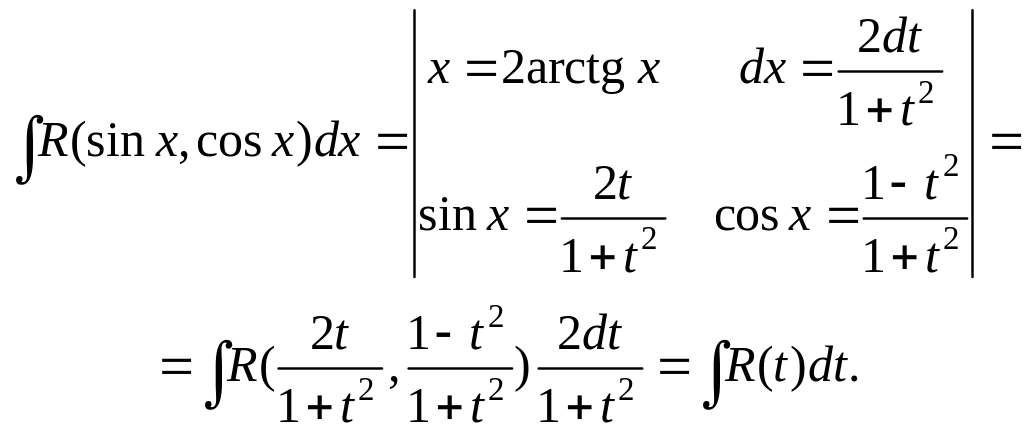
Интеграл вида
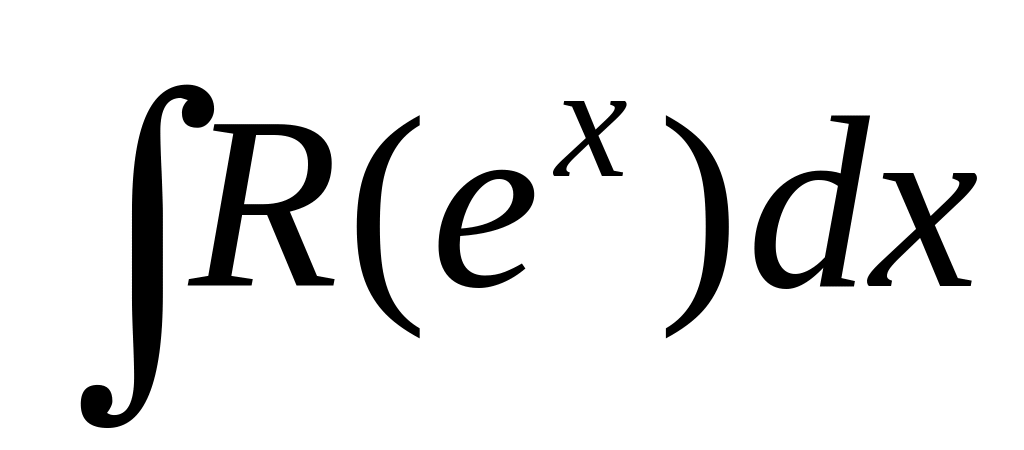 рационализируется подстановкой
рационализируется подстановкой
 Действительно,
Действительно,

Практическое занятие 10
