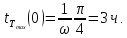4. Анализ решения задачи о суточном ходе температуры воздуха

Выберем одну из форм записи решения, например, через функцию косинуса

(4.1)

Анализ формулы (4.1) показывает, что отклонение температуры воздуха на высоте в конкретный момент времени от ее среднесуточного значения имеет вид гармонической функции

(4.2)

где

	(4.3)
	(4.4)

Здесь – амплитуда колебаний температуры воздуха на произвольной высоте , – фаза упомянутых колебаний.

Вычислим амплитуду и фазу колебаний на поверхности, то есть при

	(4.5)
	(4.6)

Из соотношений (4.5) и (4.4) следует, что колебания температуры на поверхности описываются выражением

(4.7)

Из формулы (4.5) можно определить факторы, влияющие на величину амплитуды колебаний температуры подстилающей поверхности.

Амплитуда суточного хода температуры подстилающей поверхности прямо пропорциональна амплитуде колебаний радиационного баланса 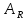. Соответственно на суточный ход влияют все факторы, влияющие на амплитуду радиационного баланса. Например, существенное влияние на амплитуду радиационного баланса оказывает облачность.

Амплитуда колебаний температуры подстилающей поверхности существенным образом зависит от коэффициента турбулентности 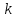. При сильно развитой турбулентности тепло быстро распространяется по вертикали, благодаря чему амплитуда суточных колебаний температуры поверхности оказывается сравнительно малой.

Амплитуда колебаний температуры подстилающей поверхности зависит от теплофизических свойств почвы: температуропроводности , объемной теплоемкости , теплопроводности . Если почва обладает хорошей теплопроводностью, то днем значительная доля тепла уходит в нижележащие слои. Соответственно доля тепла, идущая на теплообмен воздуха, уменьшается, и максимум температуры в ее суточном ходе оказывается достаточно низким. Поэтому суточный ход температуры над хорошо проводящей почвой оказывается более сглаженным, чем над почвой с малой теплопроводностью.

Из сравнения формул (4.3) и (4.5) следует, что

(4.8)

Соотношение (4.8) описывает затухание амплитуды колебаний температуры с высотой. Скорость затухания амплитуды колебаний определяется величиной

(4.9)

которую называют коэффициентом затухания. Чем больше коэффициент , тем быстрее убывает амплитуда колебаний с высотой. Из формулы (4.9) видно, что коэффициент затухания обратно пропорционален корню из коэффициента турбулентности

(4.10)

Это означает, что чем интенсивнее турбулентный обмен, тем медленнее затухают колебания температуры с высотой, что вполне физически обоснованно. При интенсивном обмене тепло быстро распространяется по вертикали, в результате чего суточный ход температуры выражен в достаточно мощном по вертикали слое. Слой атмосферы, в котором хорошо выражены суточные колебания температуры, обусловленные турбулентным обменом с подстилающей поверхностью, называют тепловым пограничным слоем. Иными словами, этот той слой, выше которого колебания отсутствуют.

Из анализа затухания амплитуды колебаний температуры получают количественную оценку теплового пограничного слоя. Из (4.8) следует, что отношение амплитуды 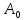к амплитуде 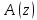описывается следующим соотношением

(4.11)

При практических расчетах высоты теплового пограничного слоя считается, что колебания отсутствуют, если их амплитуда уменьшилась по сравнению с амплитудой у поверхности в раз. Тогда

(4.12)

Логарифмируем соотношение (4.12)

(4.13)

Разрешая (4.13) относительно высоты, получаем

(4.14)

Из оценки (4.14) видно, что высота теплового пограничного слоя обратно пропорциональна коэффициенту затухания .

Заметим, что аналогичную оценку можно получить для глубины деятельного слоя почвы

(4.14)

Сравним 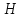и

(4.15)

Подставляя характерные значения и , получаем

То есть толщина теплового пограничного слоя атмосферы в сотни раз превосходит толщину деятельного слоя почвы. Это связано только с тем, что интенсивность турбулентного обмена теплом на порядки выше интенсивности молекулярного.

Рассмотрим сдвиг фазы колебаний температуры. Он обусловлен тем, что тепло распространяется в среде с конечной скоростью, следовательно, воздух нагревается от подстилающей поверхности с некоторым инерционным запаздыванием.

Сравним моменты времени и , в которые наблюдается фиксированная фаза температура на земной поверхности и на произвольной высоте 𝑧. Поскольку для фиксированной фазы колебаний косинус должен быть величиной постоянной (некоторой константой 𝐶)

(4.15)

то

(4.16)

Из формулы (4.16) следует, что запаздывание наступления некоторой фазы колебаний температуры удовлетворяет соотношению

(4.17)

Таким образом, фиксированная фаза колебаний температуры наступает тем позже, чем больше высота (зависимость линейная). До заданной высоты фиксированная фаза колебаний температуры распространяется тем быстрее, чем больше коэффициент турбулентности. Поскольку за время фиксированная фаза колебаний температуры распространяется от земной поверхности до высоты фазовая скорость температурной волны равна

(4.18)

Проанализируем время наступления фазы максимума температуры. В задаче о суточном ходе температуры отсчеты времени ведутся от момента наступления максимума радиационного баланса, что имеет место в истинный полдень при максимальной высоте солнца за сутки. Обращаясь к соотношению (4.7), описывающему колебания температуры на поверхности, заключаем что ее максимум имеет место, когда

(4.19)

Это в свою очередь имеет место, если

(4.20)

Отсюда

(4.21)

то есть наступает через 3 часа после максимума радиационного баланса.

Руководствуясь соотношением (4.17), получаем, что максимум температуры на произвольной высоте наступает в момент времени

(4.22)

Прибавляя 12 часов, перейдем к астрономическому времени

(4.23)