2.1 Мысал үшін үйрету тізбегі
x1 |
x2 |
d(x) |
2 2 0 -2 -2 0 4 |
1 2 6 8 0 0 -20 |
1 1 1 -1 -1 -1 -1 |
2.1.3 Адалайн моделі
Адалайн нейронының құрылымы 2.8 -суретте көрсетілген. Персептронның үлгiсiне бұл нейронның сызбасы өте ұқсас, үйрену алгоритмдері ғана өзгешеленедi.Адлайн нейронының үлгілі сигналы d нейронның сызықты бөлігінің шығысындағы s сигналымен салыстырылады.
Қателік келесідей өрнектеледі
(2.23)
Нейронды үйрету функцияның минимал шамасына әкеледі
(2.24)
2.8-сурет. Адлайн нейронының құрылымы
Қателік өлшемі дегеніміз орташа квадратты қателігі. Салмақ модификациясы үшін градиентті алгоритмдерді пайдаланады, оның мақсаттық функциясы диффенциалданады. Бұл функцияны минимал шамаға жеткізу үшін жедел түсу әдісі пайдаланылады. Адлайн нейронының салмақтары келесі формулаға сәйкес модификацияланады
,
(2.25)
Мұнда Ti үйрету коэффиценті.
(2.26)
Салмақ векторының сызықтық функциясы s болғандықтан
(2.27)
(2.25) тәуелділігі келесідей
(2.29)
Мұнда δ = d - s.
Пайдаболған ереже дельта ереже деп аталады. 2.9-суретте осы ережені пайдаланатын Адлайн нейронын үйрету алгоритмінің блок-сұлбасы көрсетілген.
Адлайн нейронын аз квадратты рекурентті әдіс (Recursive Least Squares - RLS) арқылы үйретуге болады, қателік өлшемі ретінде мына теңдеу қолданылады:
(2.30)
Мұнда λ-шамасы [0,1] интервалынан таңдалатын ұмыту коэффиценті {forgetting factor).
(2.30) теңдеуінен мүшелерді анықтау дәрежесі номері өскен сайын өсіп отырады. Қателік шамасының градиентін өлшеу
(2.31)
2.9-сурет. Адлайн нейронының үйрету алгоритмінің блок-сұлбасы
Салмақтардың алынған шамасы нормаль теңдеуді қанағаттандыру керек
(2.32)
(2.32) теңдеуін былай жазуға болады
r(t) = R(t)w(t), (2.33)
мұндағы
(2.34)
(n х n) өлшемді автокорреляциялық матрица түрінде көрсетіледі, ал
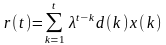(2.35)
(n х 1 ) өлшемді шығыс және үлгілі сигналдардың өзіндік корреляция векторы.
Бұл сигналдар стационар стохастикалық тәсілін орындалуын сипаттайды.(2.33) нормаль теңдеуінің шешімі, det R(t) ≠ 0 кезінде
w(t) = R-1(t) r(t). (2.36)
Матрицаның (2.36) және (6.33) нормаль теңдеуіне түрлену амалдарын болдырмау үшін RLS алгоритмін пайдаланамыз. R(t) және r(t) векторларын мына түрде жазуға болады
R(t) = λR(t-1)+x(t)xT(t); (2.37)
r(t)=λr(t-1)+x(t)d(t). (2.38)
Матрицаның қайтарымы туралы лемманы пайдаланамыз. А және В матрицалары (п x п) өлшемді матрицалары
A=B-1+CD-1CT, (2.39)
Мұнда D - (m х m)-өлшемді оң матрица; С - (п х т )- өлшемді матрица. Бұл жағдайда
A-1 = B - BC(D + CТBC)-1CТB. (2.40)
(2.40) және (2.37) формулаларын қоя отырып
А = R(t), В-1 = λR(t-1), С = x(t), D=1. (2.41)
Сондықтан
(2.42)
где
(2.43)
(2.44)
Келесі өрнекті дәлелдейік
g(t) = P(t) x(t). (2.45)
Қарапайым алгебралық амалдарын орындау нәтижесінде мынаны аламыз:
(2.46)
(2.38) және (2.36) тәуелділіктерінен
w(t) = R-1(t) r(t) = λP(t)r(t-1)+ P(t)x(t)d(t). (2.47)
(2.42) және (2.47) теңдеулерінен аламыз
w(t) = [I - g(t)xT(t)]P(t-1) r(t-1)+P(t)x(t)d(t). (2.48)
(2.38) және (2.36) арқылы аламыз
w(t) = [I - g(t)xT(t)]P(t-1)r(t-1) + P(t)x(t)d(t). (2.49)
(2.45) тәуелділігін және (2.49 теңдеуін қосу арқылы келесі рекурсияны аламыз:
w(t) = w(t-1) + g(t)[d(t) - xT (t)w(t-1)]. (2.50)
Нәтижесінде RLS алгоритмі Адалайн нейронын үйрету үшін келесі түрді қабылдайды
(2.51)
(2.52)
P(t) = λ-1[I-g(t)xT(t)]P(t-1); (2.53)
w(t) = w(t-1) + g(t)ε(t). (2.54)
Бастапқы шама ретінде мына мәндерді алуға болады
P(0) = γI, γ > 0, (2.55)
мұнда γ – тұрақты; I – бірлік матрица.