21

В А Р И А Н Т 1

Точка совершает гармонические колебания с частотой 0,5 Гц, амплитудой 5 см и нулевой начальной фазой. Для момента времени, в который смещение точки от положения равновесия равно 2,5 см,

найти:

0) скорость точки;

1) модуль ее ускорения.

По графику зависимости скорости точки от времени найти:

2) циклическую частоту колебаний точки;

3

,см/с

) ее максимальное ускорение.

0

4

10

-10

2

6

Точка колеблется по закону: Х = 0,05sin (2t) м. В момент, когда возвращающая сила достигает значения 0,005 Н, а потенциальная энергия 100 мкДж, найти:

4) фазу колебаний в радианах;

5) частоту колебаний;

6) полную энергию;

7) массу точки;

8) ее кинетическую энергию.

9. Тело, подвешенное на пружине с коэффициентом жесткости

2,5 Н/м, совершает гармонические колебания. После замены

пружины период колебаний маятника уменьшился вдвое. Найти коэффициент жесткости второй пружины.

0	1	2	3	4	5	6	7	8	9
0,136	0,246	1,57	0,157	0,926	0,3184	1,5610-4	3,12510-2	0,562510-4	10

В А Р И А Н Т 2

Тело массой 2 г совершает гармонические колебания согласно уравнению: Х = 0,03  sin ( ) t м.

0. В какой момент времени (ближайший к началу отсчета) достигается наибольшее по модулю ускорение?

Найти в этот момент времени:

1) скорость тела;

2) величину возвращающей силы;

3) кинетическую энергию тела;

4) его потенциальную энергию.

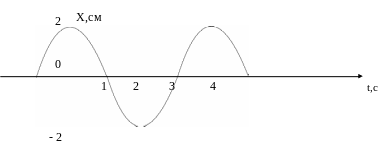
По графику колебаний пружинного маятника найти:

5) начальную фазу колебаний;

6) частоту колебаний.

7) Как относятся длины математических маятников (L₁/L₂), если за одно и тоже время первый совершает 20 колебаний, а второй - 10.

Висящий на пружине груз массой 0,1 кг совершает вертикальные гармонические колебания с амплитудой 4 см. Известно, что для упругого удлинения пружины на 1 см требуется сила 0,1 Н. Пренебрегая массой пружины, найти:

8) период колебаний;

9) полную энергию колебаний.

0	1	2	3	4	5	6	7	8	9
3	0	1,64310-5	0	2,46510-7	1,57	0,25	0,25	0,628	810-3

В А Р И А Н Т 3

Точка массой 3 г колеблется гармонически. Амплитуда колебаний равна 5 см, циклическая частота - 2 рад/с, начальная фаза равна нулю.

0. В какой момент времени скорость точки равна 0,081 м/с (впервые от начала отсчета)?

Найти в этот момент:

1) фазу колебаний (в градусах);

2) смещение точки от положения равновесия;

3) величину ускорения;

4) кинетическую энергию точки;

5) ее потенциальную энергию;

6) величину возвращающей силы.

7. По графику колебаний пружинного маятника определить его максимальное ускорение.

Тонкий обруч, повешенный на гвоздь, вбитый в стену горизонтально, колеблется в плоскости, параллельной стене. Радиус обруча 30 см.

Найти:

8) период колебаний обруча;

9) Частоту колебаний.

0	1	2	3	4	5	6	7	8	9
0,314	36	2,93910-2	0,12	9,8410-6	5,18310-6	3,52710-4	4,9310-2	1,55	0,645

В А Р И А Н Т 4

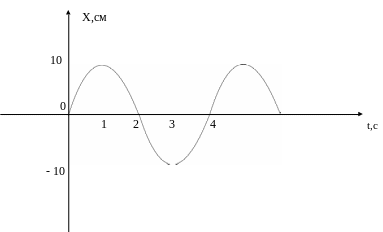
Используя график колебаний маятника, найти:

0) его максимальную скорость;

1) максимальное ускорение (модуль).

Тело массой 5 г совершает гармонические колебания. Период колебаний 2 с, амплитуда 6 см, начальная фаза равна нулю.

2. В какой момент времени смещение тела от положения равновесия

достигнет 3 см?

Найти в этот момент:

3) фазу колебаний (в градусах);

4) скорость тела;

5) величину ускорения;

6) величину возвращающей силы;

7) кинетическую энергию тела;

8) его потенциальную энергию.

К пружине подвесили грузик, в результате чего она растянулась на 9 см.

9. Каким будет период колебаний грузика, если его немного оттянуть вниз и отпустить? (Принять g = ²).

0	1	2	3	4	5	6	7	8	9
0,157	2,46510-1	0,1667	30	0,1632	0,2958	1,47910-3	6,65810-5	2,21810-5	0,6

В А Р И А Н Т 5

Уравнение движения точки массой 5 г имеет вид:

Х = 2  sin ( )  t см.

Найти:

0) максимальное значение возвращающей силы;

1. в какой момент времени (ближайший от начала отсчета) возвращающая сила достигает максимума;

2) кинетическую энергию точки в этот момент;

3) ее потенциальную энергию в этот момент.

График гармонических колебаний имеет вид:

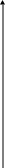
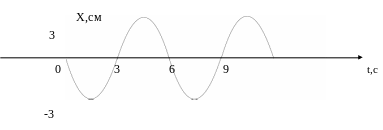
Найти в момент времени 4,5 с:

4) циклическую частоту;

5) фазу колебаний (0    2);

6) скорость;

7) ускорение (модуль).

Математический маятник длиной 99,5 см за одну минуту совершает

30 полных колебаний.

Найти:

8) период колебаний маятника;

9. ускорение свободного падения в том месте, где находится маятник.

0	1	2	3	4	5	6	7	8	9
1,09510-4	1,5	0	1,09510-6	1,047	1,57	0	3,2910-2	2	9,82

В А Р И А Н Т 6

Вагон массой 16 тонн, движущийся со скоростью 1 м/с, наталкивается на препятствие.

0. Определить величину сжатия автосцепки вагона при ударе, если известно, что пружина автосцепки сжимается на 1 см под действием силы 10⁵ Н (величина сжатия пропорционально силе).

Точка совершает гармонические колебания по закону:

Х = 5  sin (2t) см.

1. В какой момент времени возвращающая сила впервые достигнет

значения -510^-3 Н, а потенциальная энергия точки 10^-4 Дж?

Найти в этот момент времени:

2) смещение точки от положения равновесия;

3) фазу колебаний;

4) скорость точки;

5) ее ускорение (модуль);

6) массу точки.

По графику зависимости скорости колебаний от времени найти:

7) частоту колебаний;

8) амплитуду колебаний.

Однородный диск радиусом 40 см колеблется около горизонтальной оси, проходящей через край диска перпендикулярно его плоскости.

9) Каков период колебаний диска? (Принять g = ²).

0	1	2	3	4	5	6	7	8	9
0,04	0,463	0,04	0,926	0,0602	0,16	3,12510-2	0,25	0,06369	1,55

В А Р И А Н Т 7

Тело массой 10 г совершает гармонические колебания по закону, представленному на графике:

x,cм

3

0

2

4

6

t,c

-3

В момент времени 3 с найти:

0) фазу колебаний (0    2);

1) скорость тела;

2) величину ускорения;

3) величину возвращающей силы;

4) кинетическую энергию тела;

5) его полную энергию.

Железнодорожный вагон - цистерна имеет грузоподъемность

50 тонн. Цистерна укреплена на платформе, которая покоится на рессорах, опирающихся на тележки. При заливке цистерны платформа опускается на рессорах на 2,3 см. При движении поезда амплитуда качания груженой платформы на рессорах равна 1 см.

6) Найти максимальную силу давления на рельсы.

Математический маятник массой 5 г, совершающий гармонические колебания с амплитудой 2 см, обладает энергией 9,8610^-6 Дж.

Найти: