Часть 2 Построение и анализ работы комбинационных логических устройств

2.1 Задание: Необходимо построить комбинационное логическое устройство, реализующее логическую функцию которая имеет следующий вид:

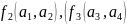
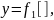
где f₁, f₂, f₃ – элементарные логические функции (считаем заданными и элементы, реализующие их);

а₁, а₂, а₃, а₄ – логические переменные.

2.2 Исходные данные

Исходными данными при реализации комбинационного устройства является логическая функция, которую должно реализовать устройство и набор логических элементов, на которых устройство будет построено.

Варианты исходных данных приведены в табл. 2.1.

Пример выбора варианта для номера зачетной книжки 77732:

- из колонки 3 имеем: а₁= х₁, а₂= х₂, а₃= 0, а₄= х_3;

- из колонки 2 имеем: f₁= И-НЕ, f₂ = И-НЕ, f₃=ИЛИ-НЕ.

Таким образом, функция, которую необходимо реализовать, имеет вид:

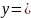х₁ х₂ ( 0 \/ х₃)

Таблица 2.1 – Исходные данные для построения комбинационного устройства

2.3 Теоретические сведения, необходимые для выполнения работы

Для выполнения работы необходимо знать основные элементарные логические функции и элементы, реализующие их, а также принципы реализации и анализа работы сложных комбинационных устройств.

Основу современных устройств обработки цифровой информации составляют цифровые (логические) ИМС.

Анализ работы цифровых устройств базируется на использовании аппарата математической логики – алгебры Джорджа Буля. В её основе лежит понятие события, которое оценивается с точки зрения его наступления: оно может произойти или не произойти.

Тогда каждое событие можно считать истинным, это может моделироваться единицей «1» (высоким уровнем напряжения при электрическом моделировании) или ложным, что моделируется нулем «0» (низким уровнем напряжения).

Обработка информации, которая подается в виде событий, ведется в двоичной системе счисления, которая имеет только две цифры:0 и 1. Величина, которая может принимать только эти два значения, называется двоичной (логической) переменной.

Сложное событие, зависящее от нескольких двоичных переменных, называется двоичной (логической) функцией:

Цифровые устройства подразделяются на два класса:

комбинационные (автоматы без памяти), где значения сигналов на выходах зависят только от комбинации сигналов на входах (шифраторы, дешифраторы, кодопреобразователи, сумматоры.);

последовательностные (автоматы с памятью), где сигналы на выходах определяются последовательностью значений входных сигналов и внутренним состоянием устройства, зафиксированного элементами памяти (регистры, счетчики).

Логическая функция И называется конъюнкцией и выполняет операцию логического умножения, (, , ):

у = х₁  х₂ = х₁  х₂ = х₁  х₂ = х₁ х₂;

f (х₁, х₂,…,х_n) = х₁х₂х₃…х_n

Функция И равна 1 только при равенстве всех аргументов 1, т.е., если х₁=1, х₂=1, х_n=1. Значения аргументов и функции записывают в таблицу, которая называется таблицей истинности. Для логической функции с n количеством входных переменных получается 2ⁿ входных комбинаций, т.е. двухэлементная функция имеет четыре входные комбинации, а трехэлементная – восемь и т.д. Часто операцию И называют операцией логического умножения (т.к. таблица истинности данной операции аналогична таблице умножения 0 и 1).

х1	х2	y = х1х2
0	0	0
0	1	0
1	0	0
1	1	1

Логическая функция ИЛИ называется дизъюнкцией и выполняет операцию логического сложения, (+,V,1):

у = х₁ V х₂; f (х₁, х₂,…,х_n) = х₁Vх₂Vх₃V…х_n.

Функция ИЛИ равна 1, если хотя бы один из аргументов х₁, или х₂, или х_n равен 1. Выражение у будет ложным только тогда, когда оба высказывания х₁ и х₂ будут ложны. Часто операцию ИЛИ называют логической суммой (т.к. первые три соотношения таблицы аналогичны сложению двух чисел).

х1	х2	y = х1V х2
0	0	0
0	1	1
1	0	1
1	1	1

Логическая функция НЕ называется инверсией и выполняет функцию логического отрицания 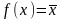( – знак инверсии).

Функция НЕ равна 1, если аргумент равен 0.

х
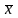
0	1
1	0

Логические элементы – это элементарные схемы, электронные модели логических функций. Соединяя эти схемы-модели между собой по определенным алгоритмам, можно построить цифровые устройства любой сложности.

Простейшие цифровые элементы должны выполнять три элементарные логические операции (сложения, умножения и отрицания), к которым можно свести любую др. операцию. Пример: ИЛИ, И, НЕ, И-НЕ, ИЛИ-НЕ.

Логический элемент И

Логический элемент, выполняющий конъюнкцию, называют логическим элементом И (конъюнктор). Логический элемент И дает на выходе напряжение только тогда, когда на все его входы подается напряжение: х₁=1; х₂=1 → у=1, в других случаях у=0.

Логический элемент ИЛИ

Функцию дизъюнкции выполняет логический элемент ИЛИ (дизъюнктор).

Результат работы логического элемента ИЛИ – появление выходного напряжения тогда, когда U подано хотя бы на один из входов, т.е. х₁=0, х₁=0→у=0, в остальных случаях у=1.

Логический элемент НЕ

Логическую функцию НЕ выполняет логический элемент НЕ.

Логический элемент НЕ имеет один вход и один выход.

Если на входе есть напряжение, которое соответствует лог. 1, то на выходе напряжение соответствует лог. 0., и наоборот, т.е. х=1→у=0; х=0→у=1.

Совокупность различных типов элементов, достаточных для воспроизведения любой логической функции, называется логическим базисом.

Элементы И, ИЛИ, НЕ называются одноступенчатыми, т.к. они реализуют одну логическую функцию.

Функцию И-НЕ (Операция Шеффера) складывают в два этапа: сначала выполняется конъюнкция входных высказываний, а потом над результатом выполняют операцию НЕ.

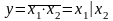
(х₁ не совместим с х₂).

Входящее высказывание		I этап	II этап
х1, х2		х1х2
х1	х2	х1х2

Функцию ИЛИ-НЕ так же складывают в два этапа: сначала выполняется дизъюнкция входных высказываний, а потом над результатом выполняют операцию НЕ.

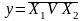
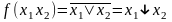
Стрелка Пирса

Входящее высказывание		I этап	II этап
х1	х2	х1vх2
0	0	0	1
0	1	1	0
1	0	1	0
1	1	1	0