4.2.3 Теплопроводность

Если слои газа имеют разную температуру, то в газе возникает перенос тепла от более нагретого слоя к менее нагретому, т.е. имеет место явление теплопроводности. Переносимой физической характеристикой является энергия молекулы, т.е.  = W, тогда уравнение (4.20) примет вид:

или в пределе при t 0, получим уравнение Фурье:

(4.24)

где dQ – количество теплоты, переносимое путем теплопроводности,  - коэффициент теплопроводности:

(4.25)

где C_V – удельная теплоемкость при постоянном объеме.

Закон Фурье: количество теплоты dQ, переносимое через площадку dS перпендикулярную направлению OX в котором убывает температура прямо пропорционально площади площадки ds, промежутку времени dt переноса и градиенту температуры .

Коэффициент теплопроводности  не зависит от давления газа.  возрастает с температурой несколько быстрее чем .

4.2.4 Внутреннее трение. Вязкость.

Если газ движется параллельно неподвижной плоскости в направлении OX, то на границе раздела скорость течения будет меняться от слоя к слою (рис. 4.3). Переносимой величиной является импульс молекулы и уравнение (4.20) примет вид:

. (4.26)

При этом на границе между двумя смежными слоями возникает сила внутреннего трения:

(4.27)

где  - коэффициент внутреннего трения (вязкость):

(4.28)

Экспериментально изучая скорость течения жидкостей и газов по трубам Гаген (в 1839 г.) и независимо от него Пуазейль (в 1841 г.) нашли, что средняя скорость ламинарного течения жидкости по трубе пропорциональна падению давления на единицу длины трубы, пропорциональна квадрату радиуса трубы и обратно пропорциональна коэффициенту вязкости:

(4.29)

Так как объем V = Sut = r²ut, где S = r² – площадь поперечного сечения трубы, то формула (4.29) примет вид:

(4.30)

Объем жидкости, протекающий по трубе, пропорционален четвертой степени радиуса трубы, времени и градиенту давления жидкости и обратно пропорционален коэффициенту вязкости жидкости.

При турбулентном течении скорость течения жидкости пропорциональна не первой степени давления, а корню квадратному из давления:

(4.31)

Эта формула носит имя французского физика Шези.  - коэффициент сопротивления течения жидкости. Формула Шези применима для труб любого сечения, а также для открытых русел рек. Формула Шези для ламинарного течения имеет следующий вид:

(4.32)

Нетрудно убедиться, что подстановка  из выражения (4.32) в формулу Шези (4.31) превращает выражение (4.31) в закон Пуазейля. Следовательно, для ламинарного течения коэффициент сопротивления убывает с увеличением скорости течения. Для турбулентного течения  почти не зависит от скорости. Опыт показывает, что закон Ньютона для вязкости применим только в пределах небольших лобовых сопротивлений в некоторых пределах значений скоростей.

При малых скоростях (до 1 м/с) лобовое сопротивление пропорционально не квадрату, а первой степени скорости. Лобовым называется сопротивление горизонтальной составляющей аэродинамической силы. Оно вычисляется по формуле Ньютона: Q = C_xSu². В этой формуле C_x – коэффициент лобового сопротивления (он различен для разных сред и тел различных форм);  - плотность среды; S – площадь – проекции тела на плоскость, перпендикулярную к скорости невозмущенного потока (так называемое «миделево сечение»); u – скорость невозмущенного потока; x – перемещение.

При больших скоростях, как мы видим Q ~ u² и коэффициент C_x нужно рассматривать как некоторую функцию вязкости среды , плотности  и линейных размеров тела. Рейнольдс предложил некоторую группу чисел, которые учитывают кинематическую вязкость среды, ее обозначают буквой :

(4.33)

где  - коэффициент вязкости. Нетрудно заметить, что если кинематические вязкости  двух сред равны, то движение тела в них испытывает одинаковое лобовое сопротивление.

Число Рейнольдса пропорционально отношению сил инерции Sv² и обратно пропорционально вязкости:

(4.34)

Благодаря вязкости тело, движущееся в жидкости, увлекает прилегающие к нему слои жидкости и потому испытывает сопротивление (трение) со стороны жидкости.

Закон Стокса: для тел шарообразной формы, движущихся с небольшой скоростью, сила трения пропорциональна коэффициенту вязкости жидкости , радиусу шара «r» и скорости движения u:

F=6ru (4.35)

На шар массой m и радиусом r, падающий со скоростью u в жидкости с вязкостью , действует три силы: сила тяжести , выталкивающая сила и сила сопротивления жидкости . С увеличением скорости движения шара, с некоторого момента времени эти силы уравновесят друг друга:

(4.36)

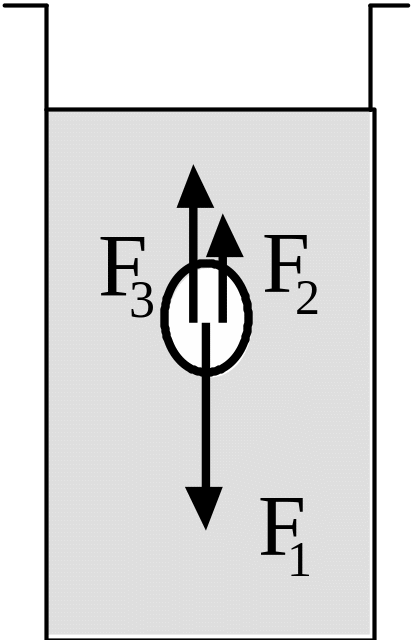
Тогда шар будет двигаться равномерно. Учитывая, что, по закону Ньютона, Архимеда и Стокса эти силы соответственно равны:

(4.37)

уравнение (3.36) перепишется в виде:

(4.38)

Отсюда:

(4.39)

(4.40)

где u – скорость молекул жидкости, ₁ – плотность тела (шара), ₂ – плотность жидкости, r – радиус тела, g – ускорение свободного падения,  - коэффициент вязкости.

Следовательно, скорость равномерного падения тела в вязкой среде тем меньше, чем больше вязкость среды и меньше размеры тела.