Глава 4. Синтаксичний аналіз

4.1. Граматики та роль синтаксичного аналізатора

Кожна мова програмування має правила, які визначають синтаксичну структуру коректних програм. В Pascal, наприклад, програма створюється із блоків, блок – з інструкцій, інструкції – з виразів, вирази – з токенів і т.д. Синтаксис конструкцій мови програмування може бути описаний за допомогою контекстно-вільних граматик або нотації БНФ (Backus-Naur Form, форм Бекуса-Наура), про яку йшла мова в главі 1. Граматики забезпечують значні переваги розроблювачам мов програмування й компіляторів, зокрема:

• Граматика дає точну й при цьому просту для розуміння синтаксичну спеціфікацію мови програмування.

• Для деяких класів граматик ми можемо автоматично побудувати ефективний синтаксичний аналізатор, що буде визначати, чи коректна структура вхідної програми. Додатковою перевагою автоматичного створення аналізатора є можливість виявлення синтаксичних неоднозначностей й інших складних для розпізнавання конструкцій мови, які інакше могли б залишитися не­ заміченими на початкових фазах створення мови та її компілятора.

• Правильно побудована граматика надає мові програмування структуру, яка сприяє полегшенню трансляції вихідної програми в об'єктний код і виявленню помилок. Для перетворення описів трансляції, заснованих на граматиці мови, у робочі програми є відповідний програмний інстру­ментарій.

• Згодом мови еволюціонують, збагачуючись новими конструкціями й виконуючи нові задачі. Додавання конструкцій у мову виявиться більше простою задачею, якщо існуюча реалізація мови заснована на його граматичному описі.

У нашій моделі компілятора, що була наведена на рис. 2.1 і відтворена нижче, синтаксичний аналізатор одержує рядок токенів від лексичного аналізатора і перевіряє, чи може цей рядок породжуватися граматикою вхідної мови. Він також повідомляє про всі виявлені помилки. Крім того, він повинен уміти обробляти звичайні помилки, що часто зустрічаються, й продовжувати роботу із частиною програми, що залишилася.

Як наводилося в розділах 2 і 3, найбільш поширеним формальним апаратом для лексичного аналізу є регулярні вирази та кінцеві автомати. Але для лексичного аналізу можна використовувати більш потужний за алгоритмічними властивостями апарат формальних граматик, який використовується при синтаксичному аналізі, тобто використовуючи апарат формальних граматик, можна, в принципі, позбавитися модуля «Лексичний аналізатор», але розробники компіляторів цього не роблять з причин, що наводилися в п. 2.1.1.

Формально граматика визначається четвіркою G=(Vn,Vt,S,P), де:

Vn і Vt - відповідно множини нетермінальних, і термінальних символів, що не перетинаються;

S - виділений символ у Vn, що звичайно називають вихідним або початковим символом;

P - кінцева множина продукцій (правил), за якими нетермінальні символи визначаються як упорядкована послідовність термінальних та/або нетермінальних символів. Ця послідовність може складатися із одного термінального або нетермінального символа. В останьому випадку це буде просте перевизначення нетермінального символа лівої частини правила.

Об'еднання множин Vn і Vt називають словником грамматики.

Для завдання продукцій частіше усього використовуються метамова (мова для опису мов) нормальних форм Бекуса-Наура або Бекусовых нормальних форм (скорочено - БНФ), яка була запропонована і вжита у 1955 р. для опису однєї з перших і на той час найбільш поширеної універсальної мови програмування АЛГОЛ. У цій метамові використовуються наступні метасинтаксичні символи або сполучення символів:

< > – кутні дужки для визначення в них імені нетермінального символу;

::= – аналог оператора присвоєння в мовах програмування. Він читається як "це є" і розділяє ліву і праву частини граматичного правила.

| – роздільник алтернативных правил у правій частині металингвістичої формули.

У лівій частині формули завжди повинний бути присутнім нетермінальний символ. Якщо в лівій частині будь-якої формули якоїсь граматики є не більш одного нетермінального символу, то така граматика є контекстно незалежною, у протилежному випадку - контекстно залежною. Далі будемо розглядати тільки контекстно незалежні граматики.

У правій частині формули записується одне або декілька (якщо вони існують) правил, розділених символом “|”, кожне з яких представляє собою, як наводилося, послідовність термінальних та/або нетермінальних символів.

Кожний нетермінальный символ повинний зустрітися в лівій частині якогось правила, тобто не може бути жодного невизначеного нетермінального символа.

Наведемо приклад граматики такого примітивного оператора присвоєння змінній значення арифметичного виразу: він складається з двох операндів і однієї з арифметичних операцій {+,-,*,/}, при цьому дужки не використовуються. Іменем змінної може бути тількі прописна літера латинського алфавіту із множини {a,b,c,d,e,f}; операндами аріфметичного виразу може бути змінна, ім’я якої складається з однієї літери з множини {a,b,c,d,e,f} або цифра. Таким чином:

Vt = {a,b,c,d,e,f,0,1,2,3,4,5,6,7,8,9,+,-,*,/}

Vn = {<оператор_присвоєння>,<змінна>,<вираз>,<операнд>,<змінна> | <ціле число без знаку>,<знак операції>,<буква>,<цифра>}

Граматика примітивного арифметичного оператора (G1)

P = {

(1) <оператор_присвоєння> ::= <змінна>:=<вираз>;

(2) <змінна> ::= <буква>

(3) <вираз> ::= <операнд><знак операції> <операнд>

(4,5) <операнд> ::= <змінна> | <ціле число без знаку>

(6) <ціле число без знаку> ::= <цифра>

(7-10) <знак операції> := +|-|*|/

(11–16) <буква> ::= a|b|c|d|e|f

(17–26) <цифра> ::= 0|1|2|3|4|5|6|7|8|9

}

S : <оператор_присвоєння> ::= <змінна>:=<вираз>;

Примітка. В дужках наведено номери правил граматики.

Нижче наведено приклади рядків, що відповідають данній граматиці:

a:=b+8; c:=1-d; b:=e*f; e:=6/4;

Тепер наведемо рядки, що не відповідають данній граматиці:

a:=6; c:=4+5+8; b:= –a+c; e1:=f/*6;

Правила граматики, що представлені БНФ, можна представити у графічній формі, що робить граматику біль наглядною. При представленні граматики у графічноій формі будемо дотримуватися таких правил (нотації):

• нетермінальні символи розміщуються у прямокутниках;

• Тетрмінальні символи роміщуються у кружках або фігурах овальної форми;

• кожна вертикальна линия відповідає одному правилу;

• горізонтальна лінія, яка має прямувати зліва направо, з’єднує термінальні та/або нетермінальні символи в правило у той послідовності, що була задана у правилі.

При такій нотації граматику G1, що представлена вище в БНФ, на рис.4.1 представлена у графічній формі.

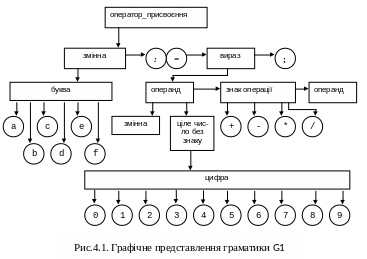
Як бачимо, крім обмеженності з-за алфавіту, в заданій граматиці є ще обмеження на кількість знаків у імені змінної й у числа (по одному знаку), а також на кількість операндів (всього два) і операторів (всього один) у виразі. На перший погляд, для зняття ціх обмежень можна обійтися простим збільшенням складових у правилах, наприклад:

<ціле число без знаку>::=<цифра>|<цифра><цифра> ,

тоді можна вже використовувати двозначні цілі числа. Але існує більш універсальний механізм розв’язання задачі розмірності граматичних конструкцій – рекурсія. У загальному випадку рекурсію можна розглядати як процес, у якій щось визначається саме через себе.

Нижче приводиться приклади рекурсивних граматик:

G2 – визначення цілого числа без знаку як сукупності цифр;

G3 – визначення ідентифікатора як сукупності літер і цифр, що починаеться з літери.

Граматика визначення цілого числа без знаку (G2):

<ціле число без знаку>::=<цифра>|<ціле число без знаку><цифра>

<цифра>::=0|1|2|3|4|5|6|7|8|9

Граматика визначення ідентифікатора (G3)

<ідентифікатор>::= <літера> | <ідентифікатор><літера> | <ідентифікатор><цифра>

<літера> ::= a|b| ... |z|

<цифра> ::= 0|1|2|3|4|5|6|7|8|9

Граматика G3 графічно представлена на рис. 4.2.

Не усі рядки, утворені з термінальних символів, представляють собою синтаксично правильні „речення” цієї мови G2 , наприклад, “a”, ”a1”, ”ghb4r” – це речення даної мови, а “4”, “ADE“– не є реченнями цієї мови.

Аналіз сполучень різноманітних елементів рядка для визначення того, чи є або не є даний рядок символів реченням мови, називається граматичним розбором. Для синтаксично правильного речення можна побудувати дерево граматичного розбору, у той час як для рядка, що не є реченням даної мови, такої схеми не існує. Покажемо дерево граматичного розбору (рис.4.3) за правилами граматики G3 для рядка “fs8” правилами мови, яка була наведена вище на рис.4.2.

Ідентифікатор

Цифра

Ідентифікатор

Ідентифікатор

Літера

Літера

Літера

s

8

f

Рис. 4.3. Дерево граматичного розбору рядка “fs8”

Наведемо ще один приклад граматики частини мови Pascal з врахуванням того, що граматику нетермінального символа “ідентифікатор” було наведено вище (див. G3). Обмежемося також трьома типами даних.

Граматика оператора визначання типу змінних у мові Pascal (G4).

<оператор_опису_змінних>::= var <список_імен_змінних> : <тип_змінних>;

<список_імен_змінних>::=<ім’я_змінної> | <список_імен_змінних>, <ім’я_змінної>

<ім’я_змінної>::= <ідентифікатор>

<тип_змінних>::= char|real|int

<ідентифікатор>:= ... (див. граматику G3).

Наведеній граматиці відповідають, наприклад, такі рядки:

var ac2: char;

var bb: int;

var c2,a, b1d: real;

У графічній формі граматика G4 представлена на рис. 4.4.

В граматиках G3 і G4 в рекурсивних правилах використовувалася ліва рекурсія. Але можна побудувати і праворекурсивні правила. Так, при визначенні ідентифікатора правила з правою рекурсиєю будуть виглядати так:

<ідентифікатор>::= <літера> | <літера><ідентифікатор> | <ідентифікатор><цифра>

А правила визначення списку імен змінних в граматиці G4 виглядали б так:

<список_імен_змінних>::= <ім’я_змінної>| <ім’я_змінної>,<список_імен_змінних>

Від використаного типу рекурсії залежить напрям розбору вхідного рядка в компіляторах: «зліва направо» чи «справа наліво».

Наведемо інші приклади граматик.

Граматика числа (G5), у якому роздільником цілої та дробової частин є кома

<число>::= <знак числа><число без знаку>|<число без знаку>

<число без знаку>::= <ціле число без знаку>,<ціле число без знаку>| <ціле число без знаку>

<ціле число без знаку>::= <цифра> | <ціле число без знаку><цифра>

<цифра>::= 0 | 1 | … |9

<знак числа>::= + | -

Граматика функції суми в електронній таблиці EXCEL (граматика G6)

<функція суми>::= =<ім’я_функції_суми>(<список діапазонів суми>)

<ім’я_функції_суми>::= SUM | sum

<список доданків суми>::= <доданок суми> | <список доданків суми>; <доданок суми>

<доданок суми>::= <діапазон комірок> | <код комірки> |<число>

<діапазон комірок>::= <код комірки>:<код комірки>

<код комірки>::= <код колонки><номер рядка>

<код колонки>::= <літера> | <літера><літера>

<літера>::=A | B | …. | Z

< номер рядка>::= <ціле число без знаку>

<число>::= див. граматику G5

<ціле число без знаку>::= див. граматику G2

У графічній формі наведена граматика представленана рис. 4.5.

Наведемо ще приклад з граматики обмеженої природньої мови (G7). Це буде граматика підмножини англійської мови:

Vn = {<речення>, <артикль>, <підмет>, <присудок>, <іменник>, <дієслово>, <прямий додаток>}

Vt = {a the Linus Charley Snoopy blanket dog song holds pets sings}

P = {

(1) <речення>::= <підмет> <присудок>

(2) <підмет>::= <артикль> <іменник>

(3) <підмет>::= <іменник>

(4) <присудок>::= <дієслово> <прямий додаток>

(5) <артикль>::= a

(6) <артикль>::= the

(7) <іменник>::= Linus

(8) <іменник>::= Charley

(9) <іменник>::= Snoopy

(10) <іменник>::= blanket

(11) <іменник>::= dog

(12) <іменник>::= song

(13) <дієслово>::= holds

(14) <дієслово>::= pets

(15) <дієслово>::= sings

(16) <прямий додаток>::= <артикль> <іменник>

(17) <прямий додаток>::= <іменник>

}

p : <речення>::= <підмет> <присудок>

Приклади рядків, які породжуються цією граматикою:

‘Charley pets a dog’

‘Linus holds the blanket’

‘Snoopy sings a song’

‘The blanket holds a dog’

Що стосується останнього речення, то хоча воно й граматично правильним, але є неправильним з точки зору семантики. Поняття семантики є і в штучних мовах, якими є мови програмування, але воно буде розглянуто пізніше.

На рис. 4.6 представлена графічна форма граматики G7.

На даному рисунку, крім термінальних і не термінальних символів, що представлені відповідно у прямокутниках та у не прямокутних фігурах, наведено ще й номери правил. Оскільки в граматиці G7 відсутні рекурсивні правила, то кількість рядків, що можуть бути породжені нею, буде скінченою величиною, і в даному випадку вона дорівнює 972.

Є три основних типи синтаксичних аналізаторів граматик, серед яких такі, що використовують універсальні методи розбору, такі як алгоритми Кока-Янгера-Касами або Эрли, можуть працювати з будь-якою граматикою. Однак ці методи занадто неефективні для використання в промислових компіляторах. Методи, які звичайно застосовуються в компіляторах, класифікуються як спадні (згори до низу, top-down) або висхідні (знизу нагору, bottom-up).

У спадному (низсхідному) граматичному розборі побудова синтаксичного дерева починається з кореня дерева (тобто з виділеного символу ) і продовжується униз до листя, тобто до термінальних символів аналізованого рядка. Ціль такого процесу складається в тому, щоб систематично породжувати правила мови доти, поки не буде отримане речення, що збігається з аналізованим рядком. При цьому, можливо, прийдеться повертатися назад, якщо вибраний раніше ланцюжок побудови дерева виявився тупиковим. Щоб уникнути частих повернень назад, розроблені різноманітні варіанти проглядів вперед. Чим складніше граматика мови, тим більшою має бути 'дистанція' прогляду.

Породження правила можна відобразити за допомогою символу →, для якого запис 'x → y' інтерпретується як "рядок 'x' породжує рядок 'y'”.

Приклад 4.1. Покажемо метод спадного граматичного розбору на прикладі граматики обмеженої природної (англійської) мови (G7), яка наводилася у главі 1.

(1) <речення>::= <підмет> <присудок>

(2) <підмет>::= <артикль> <іменник>

(3) <підмет>::= <іменник>

(4) <присудок>::= <дієслово> <прямий додаток>

(5) <артикль>::= a

(6) <артикль>::= the

(7) <іменник>::= Linus

(8) <іменник>::= Charley

(9) <іменник>::= Snoopy

(10) <іменник>::= blanket

(11) <іменник>::= dog

(12) <іменник>::= song

(13) <дієслово>::= holds

(14) <дієслово>::= pets

(15) <дієслово>::= sings

(16) <прямий додаток>::= <артикль> <іменник>

(17) <прямий додаток>::= <іменник>

Як бачимо, в цій граматиці іменники, дієслова й артиклі виступають як термінальні символи, тобто їх «розпізнали» на стадії лексичного аналізу.

Розглянемо рядок ‘Linus holds the blanket’. Основна ідея спадного методу розбору полягає в тому, що продукція розглядається як правило, що переписує нетермінал з лівої частини і заміщує його рядком із правої частини продукції. Таке заміщення називається породженням, яке більш детально буде розглянуте далі. Кроки цього породження для вказаного рядка за граматикою G7 наведено нижче. Ліворуч кожного породження наведено номер використаної продукції граматики.

(1) <речення> → <підмет> <присудок>

(3) <підмет> <присудок> → <іменник> <присудок>

(7) <іменник> <присудок> → Linus <присудок>

(7) Linus <присудок> → Linus <дієслово> <прямий додаток>

(13) Linus <дієслово> <прямий додаток> → Linus holds <прямий додаток>

(16) Linus holds <прямий додаток> → Linus holds <артикль> <іменник>

(6) Linus holds <артикль> <іменник> → Linus holds the <іменник>

(10) Linus holds the <іменник> → Linus holds the blanket

На рис. 4.7 представлено дерево граматичного розбору цього рядка згідно з граматикою. А для рядка ‘Linus the a holds’ таке дерево побудувати не можливо, тому воно є граматично неправильним.

При підіймальному (висхідному) граматичному розборі побудова синтаксичного дерева починається з "листя" (висячих вершин синтаксичного графа, якими є нетермінальні символи граматики) і продовжується просуванням нагору до кореня. При такому алгоритмі запис 'x → y' інтерпретується як 'у' зводиться до 'х'. Це так зване зворотне породження. Кроки цього породження для того ж самого рядка ‘Linus holds the blanket’ за граматикою G7 наведено нижче.

Приклад 4.2. Як і для прикладу спадного методу розбору цього рядка ліворуч кожного породження наведено номер використаної продукції граматики.

(7) <іменник> holds the blanket → Linus holds the blanket

(3) <підмет> holds the blanket → <іменник> holds the blanket

(13) <підмет> <дієслово> the blanket → <підмет> holds the blanket

(6) <підмет> <дієслово> <артикль> blanket → <підмет> <дієслово> the blanket

(10) <підмет> <дієслово> <артикль> <іменник> → <підмет> <дієслово> <артикль> blanket

(16) <підмет> <дієслово> <прямий додаток> → <підмет> <дієслово> <артикль> <іменник>

(4) <підмет> <присудок> → <підмет> <дієслово> <прямий додаток>

(1) <речення> → <підмет> <присудок>

Таким чином, як виявляється з назв, спадні синтаксичні аналізатори будують дерево розбору зверху (від кореня) униз (до листя), тоді як висхідні починають із листя і йдуть до кореня. Найбільш ефективні спадні й висхідні методи працюють тільки з підкласами граматик, однак деякі із цих підкласів, такі як LL-граматики і LR-граматики (абревіатури будуть розкриті нижче), досить виразні для опису більшості синтаксичних конструкцій мов програмування. Реалізовані вручну синтаксичні аналізатори частіше працюють із LL-граматиками. Синтаксичні аналізатори для трохи більш широкого класу LR-граматик, як правило, створюються за допомогою автоматизованих інструментів (YACC, BIZON та інші).

Наведемо приклади розбору за граматикою визначення змінних мовою Pascal.

(1) <оператор_опису_змінних>::= var <список_імен_змінних> : <тип_змінних>;

(2) <список_імен_змінних>::= <ідентифікатор>

(3) <список_імен_змінних>::= <список_імен_змінних>’ <ідентифікатор>

(4) <тип_змінних> ::= char

(5) <тип_змінних>::= real

(6) <тип_змінних>::= int

(7) <ідентифікатор> ::= <літера>

(8) <ідентифікатор> ::= <ідентифікатор> <літера>

(9) <ідентифікатор> ::= <ідентифікатор> <цифра>

(10) <літера> ::= a

(11) <літера> ::= b

..................................

(35) <літера> ::= z

(36) <цифра> ::= 0

(37) <цифра> ::= 1

(38) <цифра> ::= 2

…………………..

(45) <цифра> ::= 9

Хай на вході синтаксичного аналізатора є вхідний рядок:

var a, z2, ba : char;

Спадний розбір зліва направо.

(1) <оператор_опису_змінних> → var <список_імен_змінних> : <тип_змінних>;

(3) var <список_імен_змінних> : <тип_змінних>; → var <список_імен_змінних>, <ідентифікатор> : <тип_змінних>;

(3) var <список_імен_змінних> , <ідентифікатор>: <тип_змінних>; → var <список_імен_змінних>, <ідентифікатор> , <ідентифікатор>: <тип_змінних>;

(2) var <список_імен_змінних>, <ідентифікатор> , <ідентифікатор>: <тип_змінних>; → var <ідентифікатор> , <ідентифікатор> , <ідентифікатор>: <тип_змінних>;

(7) var <ідентифікатор> , <ідентифікатор> , <ідентифікатор>: <тип_змінних>; → var <літера> , <ідентифікатор> , <ідентифікатор>: <тип_змінних>;

(10) var <літера> , <ідентифікатор> , <ідентифікатор>: <тип_змінних>; → var a, <ідентифікатор> , <ідентифікатор>: <тип_змінних>;

(9) var a, <ідентифікатор> , <ідентифікатор>: <тип_змінних>; → var a, <ідентифікатор> <цифра> , <ідентифікатор>: <тип_змінних>;

(7) var a, <ідентифікатор> <цифра> , <ідентифікатор>: <тип_змінних>; → var a, <літера> <цифра> , <ідентифікатор>: <тип_змінних>;

(35) var a, <літера> <цифра> , <ідентифікатор>: <тип_змінних>;→ var a, z <цифра> , <ідентифікатор>: <тип_змінних>;

(38) var a, z <цифра> , <ідентифікатор>: <тип_змінних>; → var a, z2, <ідентифікатор>: <тип_змінних>;

(8) var a, z2, <ідентифікатор>: <тип_змінних>; → var a, z2, <ідентифікатор><літера>: <тип_змінних>;

(7) var a, z2, <ідентифікатор><літера>: <тип_змінних>; → var a, z2, <літера> <літера>: <тип_змінних>;

(11) var a, z2, <літера> <літера>: <тип_змінних>; → var a, z2, b<літера>: <тип_змінних>;

(10) var a, z2, b<літера>: <тип_змінних>; → var a, z2, ba : <тип_змінних>;

(4) var a, z2, ba : <тип_змінних>; → var a, z2, ba : char;

Вектор граматического разбора <1,3,3,2,7,10,9,35,38,8,7,11,10,4>

Висхідний розбір зліва направо.

(10) var <літера>, z2, ba : char; → var a, z2, ba : char;

(7) var <ідентифікатор>, z2, ba : char; → var <літера>, z2, ba : char;

(2) var <список_імен_змінних> , z2, ba : char; → var <ідентифікатор>, z2, ba : char;

(35) var <список_імен_змінних> , <літера>2, ba : char;→ var <список_імен_змінних> , z2, ba : char;

(7) var <список_імен_змінних> , <ідентифікатор>2, ba : char;→ var <список_імен_змінних> , <літера>2, ba : char;

(38) var <список_імен_змінних> , <ідентифікатор> <цифра>, ba : char;→ var <список_імен_змінних> , <ідентифікатор>2, ba : char;

(9) var <список_імен_змінних> , <ідентифікатор>, ba : char;→ var <список_імен_змінних> , <ідентифікатор> <цифра>, ba : char;

(3) var <список_імен_змінних>, ba : char;→ var <список_імен_змінних> , <ідентифікатор>, ba : char;

(11) var <список_імен_змінних>, <літера>a : char;→ var <список_імен_змінних>, ba : char;

(7) var <список_імен_змінних>, <ідентифікатор>a : char;→ var <список_імен_змінних>, <літера>a : char;

(10) var <список_імен_змінних>, <ідентифікатор><літера> : char; → var <список_імен_змінних>, <ідентифікатор>a : char;

(8) var <список_імен_змінних>, <ідентифікатор> : char; → var <список_імен_змінних>, <ідентифікатор><літера> : char;

(3) var <список_імен_змінних> : char; → var <список_імен_змінних>, <ідентифікатор> : char;

(4) var <список_імен_змінних> : <тип_змінних>; → var <список_імен_змінних> : char;

(1) <оператор_опису_змінних> → var <список_імен_змінних> : <тип_змінних>;

Вектор граматического разбора <10,7,2,35,7, 38,9,3,11,7,10,8,3,4,1>,

а був <1,3,3,2,7,10,9,35,38,8,7,11,10,4>

Вище було показано, що синтаксичний аналіз можна повністю виконати за допомогою апарату формальних граматик без лексичного аналізатора, але, як неодноразово підкреслювалося, це не ефективно. Покажемо на прикладі.

Граматика оператора присвоєння арифметичного виразу

1 <оператор присвоєння АВ> ::= <ідентифікатор>:= <перший знак АВ><АВ>;

2 <оператор присвоєння АВ> ::= <ідентифікатор>:= <АВ>;

3 <АВ> ::= <складове>

4 <АВ> ::= <АВ><знак дод/відн><складове>

5 <складове> ::= <множник>

6 <складове> ::= <складове><знак множ/діл><множник>

7 <множник> ::= <ідентифікатор>

8 <множник> ::= <число без знаку>

9 <множник> ::= (<АВ>)

10 <ідентифікатор> ::= <літера>

11 <ідентифікатор> ::= <ідентифікатор><літера>

12 <ідентифікатор> ::= <ідентифікатор><цифра>

13 <літера> ::= a

14 <літера> ::= b

...................

38 <літера> ::= z

39 <цифра> ::= 0

40 <цифра> ::= 1

...................

49 <цифра> ::= 9

50 <число без знаку> ::= <ціле число без знаку>.<ціле число без знаку>

51 <число без знаку > ::= <ціле число без знаку>

52 <ціле число без знаку> ::= <цифра>

53 <ціле число без знаку> ::= <ціле без знаку><цифра>

54 <знак дод/відн> ::= +

55 <знак дод/відн> ::= -

56 <знак множ/діл> ::= *

57 <знак множ/діл> ::= /

58 <перший знак АВ> ::= +

59 <перший знак АВ> ::= -

Тепер визначимо наступні токени та їх граматики (див. табл. 1.1).

Таблиця 1.1.

Токен	Позна-чення токена	Нетермінальний символ у попередніх граматиках	Граматика нетермінального символу	Номери правил у граматиці G8
Ідентифікатор	id	<ідентифікатор>	G2	9– 47
Число	num	<чісло>	G9	38–51
Знак додавання/віднімання	sum_op	<знак дод/відн>	G10	52,53
Знак множення/ділення	mult_op	<знак множ/діл>	G11	54,55

Кожний токен представлений множиною правил, номера яких наведено у таблиці 1.1. Після лексичного аналізу виявлені лексеми вже можна розглядати як термінальні символи, тоді граматику оператора присвоєння арифметичного виразу G8 можна представити наступними правилами (токени виділені жирним шрифтом):

1 <оператор присвоєння АВ> ::= id:= <перший знак АВ><АВ>;

2 <оператор присвоєння АВ> ::= id:= <АВ>;

3 <АВ> ::= <складове>

4 <АВ> ::= <АВ> sum_op <складове>

5 <складове> ::= <множник>

6 <складове> ::= <складове> mult_op <множник>

7 <множник> ::= id

8 <множник> ::= num

9 <множник> ::= (<АВ>)

10 <перший знак АВ>: := +

11 <перший знак АВ>::= -

В результаті, замість 59 правил граматики G6 одержали 11 правил, що істотно полегшує синтаксичний аналіз.

Таким чином, як виявляється з назв, спадні синтаксичні аналізатори будують дерево розбору зверху (від кореня) униз (до листя), тоді як висхідні починають із листя і йдуть до кореня. Найбільш ефективні спадні й висхідні методи працюють тільки з підкласами граматик, однак деякі із цих підкласів, такі як LL-граматики і LR-граматики (абревіатури будуть розкриті нижче), досить виразні для опису більшості синтаксичних конструкцій мов програмування. Реалізовані вручну синтаксичні аналізатори частіше працюють із LL-граматиками. Синтаксичні аналізатори для трохи більш широкого класу LR-граматик, як правило, створюються за допомогою автоматизованих інструментів (YACC, BIZON та інші).

У цій главі вважається, що вихід синтаксичного аналізатора є деяким поданням дерева розбору вхідного потоку токенів, виданого лексичним аналізатором. На практиці є низка задач, які можуть супроводжувати процес розбору, - наприклад, збір інформації про різні токени у таблиці символів, виконання перевірки типів й інших видів семантичного аналізу, а також створення проміжного коду. Всі ці задачі представлені одним блоком "Інші задачі початкової фази компіляції" на рис. 4.1. Детальніше вони будуть обговорюватися у наступних главах.