Силы в зацеплении косозубой передачи

Нормальную силу F_n в зацеплении можно разложить на три состав­ляющие (рис. 5.2, а):

где F, — окружная сила,

F _r — радиальная сила, F_a — осевая сила,

• При работе косозубых передач зубья входят в зацепление не сразу по всей длине, а постепенно.

• Передаваемая нагрузка распределяется на несколько зубьев.

• В зацеплении всегда находятся минимум две пары зубьев.

• По сравнению с прямозубыми передачами повышаются нагру­зочная способность, плавность и бесшумность работы. Косозубые переда­чи широко применяют в технике.

• С увеличением угла наклона увеличиваются длина контактной ли­нии и коэффициент перекрытия, т. е. плавность и бесшумность работы повышаются.

• Одновременно увеличивается осевое усилие, дополнительно нагружающее валы и подшипники.

• Д ля ограничения осевых сил угол наклона выбирают в диапазоне 8...20°, стандартные косозубые колеса изготовляют с углом β < 15°.

Для уравновешивания осевых усилий применяют цилиндрические колеса с венцами, разделенными на участки с правым и левым зубом, — шевронные колеса. В шевронном колесе осевые силы на полушевронах направлены в разные стороны (рис. 5.2, б): они уравновешиваются внутри колеса и не передаются на валы и опоры. Углы наклона на шев­ронных колесах увеличивают до 35°, иногда больше. Недостатком шев­ронных колес является их высокая стоимость.

Расчет косозубых колес на контактную прочность и изгиб

П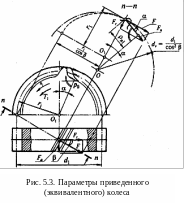 роектировочный расчет по контактным напряжениям

Профиль косого зуба в нормальном сечении совпадает с профилем прямого зуба т_п = т. В колесах с косым зубом стандартизирован нор­мальный модуль. При получении формул для расчета на прочность косозубого колеса используют эквивалентное прямозубое колесо, у которо­го форма зуба совпадает с формой зуба в нормальном сечении косозубого колеса, радиус равен радиусу кривизны эллипса, полученного в сечении п—п зуба косозубого колеса. Эквивалентное колесо изображе­но на рис. 5.3.

Параметры эквивалентного колеса определяют по формулам:

делительный диаметр

где следовательно,

число зубьев

Ширина эквивалентного прямозубого колеса равна длине зуба косозубого колеса.

Для расчета на прочность по контактным напряжениям и на изгиб используем формулы для прямозубого колеса. Подставив параметры эквивалентного колеса, получим формулу для проектировочного расче­та передачи:

Для косозубых передач К_а = 43 МПа^1/3. Косозубые передачи работа­ют более плавно, поэтому коэффициент К_Hβ меньше, чем у прямозубых.

Допускаемые напряжения рассчитывают так же, как для прямозу­бых колес.

Полученное значение межосевого расстояния округляют до ближай­шего стандартного значения, определяют геометрические параметры колес и проверяют полученную передачу по контактным напряжениям.

Некоторые рекомендации по параметрам редукторов помещены в табл. П9 Приложения.

Проверочный расчет по контактным напряжениям выполняют по формуле

где К_На, К_щ, K_Hv, K_Fa, К_п, K_Fv — коэффициенты нагрузки (см. расчет прямозубых передач).

Если условие не выполняется, увеличивают ширину колеса b₂; если этого недостаточно, увеличивают межосевое расстояние.

Проверка на изгиб

Наклонное положение зубьев увеличивает их прочность на изгиб и плавность работы. Для расчета косозубых колес используют формулу для прямозубых и вводят поправочный коэффициент Y_fβ — коэффици­ент, учитывающий наклон зуба, Y_β = 0,7...0,9.

Проверку на изгиб косозубых колес выполняют по формуле

Коэффициент формы зуба Y_F определяют по таблицам прямозубых колес по числу зубьев эквивалентного колеса

Допускаемое напряжение [a_f] определяется так же, как для прямо­зубых колес.

Для обеспечения равной прочности по контактным напряжениям и на изгиб можно определить нормальный модуль передачи по формуле

где a_w — полученное при расчете по контактным напряжениям межосе­вое расстояние; b₂ = ψ_baa_w.