5.2.4. Скидка на количество

Очень часто, если заказываемое количество товара больше определенного числа, предоставляется скидка. В этом случае снижаются расходы на закупку, но увеличиваются затраты на хранение.

Общие издержки = закупка + издержки TC(q) = CD +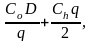 (5.5)

где С - закупочная цена.

Необходимо выяснить, стоит ли воспользоваться скидкой.

Пример 5.3. Предприятие закупает песок у поставщика. Годовой объем спроса предприятия составляет 6400 т. При увеличении объема партии заказа поставщик предоставляет покупателям скидки с цены с целью побуждать их делать закупки в больших количествах.

Расходы на размещение и выполнение заказа составляют 100 тыс.руб., а затраты на хранение на складе 1 т песка в год – 8 тыс.руб.

Определить:

1. Экономичную партию заказа песка без учета скидок с цены, а также полные затраты, включающие расходы на закупку, на размещение и выполнение заказа, а также хранение запасов сырья;

2. Полные затраты предприятия в соответствии с теми объемами заказа песка, которые превышают экономичный размер заказа и в цене продажи которых заложены скидки;

3. Выберите значение партии заказа, обеспечивающее минимальную величину полных затрат, включающих расходы на закупку сырья, на размещение и выполнение заказа, а также на хранение сырья на складе предприятия.

Решение:

Экономичная партия заказа без учета скидок:

q =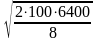 = 400 т.

При партии заказа, равной 400 т полные затраты составят

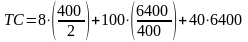= 259200 тыс.руб.

При партии заказа, равной 500 т:

= 258640 тыс.руб.

При партии заказа, равной 1000 т:

= 259360 тыс.руб.

В результате получаем, что партия заказа песка, обеспечивающая минимальную величину полных затрат, составляет 500 т.

5.2.5. Модель производства партии продукции

Ранее была рассмотрена модель экономичного размера партии (сначала товар производят, потом используют и т. д.). Разрешим теперь использование товара по мере его производства (рис. 5.3).

Рисунок 5.3 - Модель производства партии продукции

Пусть Р — темп производства, D — темп использования. Произведя q единиц продукции, производство прекращаем. Так как мы начинаем использовать произведенную продукцию сразу же, не дожидаясь остановки производства, то в момент этой остановки на складе будет не q единиц (как в модели экономичного размера партии), а меньше.

Издержки ТС = стоимость организации технологического процесса + хранение = 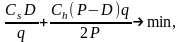(5.6)

где q - экономичный размер партии.

Решение этой задачи:

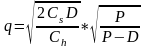. (5.7)

5.2.6. Модель планирования дефицита

В некоторых случаях издержки хранения являются очень высокими, поэтому имеет смысл допустить регулярные интервалы времени, когда товар на складе отсутствует.

Издержки ТС = подача заказов + хранение + штраф за дефицит. (5.8)

Возможны два подхода:

1) полученная новая продукция не идет на выполнение заявок на товар во время его отсутствия;

2) часть полученной новой продукции идет на погашение всех заявок, оставленных во время отсутствия запасов.

Рассмотрим эти случаи подробнее.

1. Случай невыполнения заявок (рис. 5.4).

Рисунок 5.4 - Случай невыполнения заявок

S — максимальный размер дефицита (максимально возможное число единиц товара, которое могло бы быть реализовано за время его отсутствия в каждом цикле). На графике периоды дефицита условно изображаются ниже оси времени. С_b — годовая стоимость отсутствия единицы продукции в запасе (потеря доверия клиентов, непроданная продукция и т. д.).

Издержки ТС — подача заказов + хранение + штраф за дефицит = (5.9)

где q - оптимальный размер заказа;

S — максимальный размер дефицита.

Решениями этой задачи будут величины:

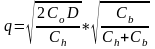; (5.10)

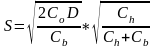. (5.11)

2. Случай выполнения заявок (рис. 5.5).

В случае выполнения заявок максимальный уровень запасов будет равен не q, а (q - S).

Рисунок 5.5 - Случай выполнения заявок

Издержки ТС — подача заказов + хранение + штраф за дефицит = 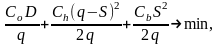(5.12)

где q - оптимальный размер заказа;

S - максимальный размер дефицита.

Решениями этой задачи будут величины:

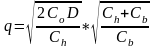; (5.13)

. (5.14)