
- •Экономика и управление ресурсами организации Учебное пособие
- •Содержание
- •1. Сущность и организация управления ресурсами на предприятии 5
- •Введение
- •1. Сущность и организация управления ресурсами на предприятии
- •1.1. Особенности и роль ресурсов в бизнесе
- •1.2. Виды, структура и классификация ресурсов. Система управления ресурсами
- •2. Доходы, расходы и прибыль коммерческой организации
- •3.Структура капитала и дивидендная политика
- •3.1. Сущность и классификация капитала
- •3.2. Принципы формирования и оценки стоимости капитала
- •3.3. Стоимость капитала и принципы его оценки
- •3.Стоимость капитала предприятия служит базовым показателем эффективности финансового инвестирования.
- •3. Оптимизация структуры капитала по критерию максимизации уровня финансовой рентабельности.
- •5. Оптимизация структуры капитала по критерию минимизации уровня финансовых рисков.
- •6. Формирование показателя целевой структуры капитала.
- •3.3. Сущность и виды дивидендной политики
- •4. Модели формирования портфеля ценных бумаг
- •4.1. Модель оценки капитальных активов
- •4.2. Модель теории арбитражного ценообразования
- •4.3. Анализ доходности международного портфеля ценных бумаг
- •5. Управление оборотным капиталом предприятия
- •5.1. Понятие и структура оборотного капитала
- •5.2. Управление запасами
- •5.2.1. Основные понятия
- •5.2.2. Основная модель управления запасами
- •5.2.3. Модель экономичного размера партии
- •5.2.4. Скидка на количество
- •5.2.5. Модель производства партии продукции
- •5.2.6. Модель планирования дефицита
- •5.3. Управление денежными средствами
- •5.3.1. Политика управления денежными потоками
- •5.3.2. Направления и методы оптимизации денежных потоков
- •Заключение
- •Рекомендованная литература
- •Экономика и управление ресурсами организации
- •443030, Самара, ул.Аксакова, 21
5.2. Управление запасами
5.2.1. Основные понятия
Выбирается промежуток времени 1 год. Рассматривается модель одиночного склада. Считается, что на складе хранится запас однотипных изделий (однономенклатурный запас). Спрос на эти изделия может быть постоянным или случайным. Пополняться склад может либо периодически (циклическая модель), либо при снижении запасов до некоторого уровня (уровневая модель).
Объем заказа — это количество заказываемых изделий. Уровень повторного заказа — количество изделий на складе, при котором подается заказ на новые изделия. Время поставки может быть либо мгновенным, либо фиксированным, либо случайным. Штраф за дефицит — это убытки, связанные с отсутствием запаса.
За хранение каждой единицы запаса берется определенная плата Сh. D - годовой спрос на изделия. Стоимость подачи заказа Со — это накладные расходы, связанные с реализацией заказа (затраты на подготовительно-заготовочные операции, не зависят от объема заказа). Вся теория будет строиться с целью минимизации суммарных издержек.
5.2.2. Основная модель управления запасами
Предпосылки основной модели: 1) спрос равномерный и постоянный; 2) время поставки постоянно; 3) отсутствие запасов недопустимо; 4) каждый раз заказывается постоянное количество - оптимальный размер заказа (рис. 5.1).

Рисунок 5.1 – Основная модель управления запасами
Издержки
ТС = подача заказов + хранение
=
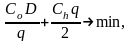 (5.1)
(5.1)
где q — оптимальный размер заказа;
q/2 — средний объем хранимого запаса.
Решением этой оптимизационной задачи будет значение:
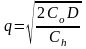 .
(5.2)
.
(5.2)
Пример 5.1. На фирме используется 400 единиц товара в месяц, стоимость каждого заказа равна 200 тыс.руб., стоимость хранения каждой единицы товара – 10 тыс.руб.
Определить:
Чему равен оптимальный размер заказа?
Сколько заказов следует делать в месяц?
Как часто необходимо делать каждый заказ?
Чему равен оптимальный средний размер товарного запаса?
Решение:
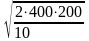 =
127 шт.;
=
127 шт.;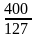 =
3 заказа в месяц;
=
3 заказа в месяц;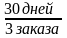 =
каждые 10 дней.
=
каждые 10 дней.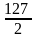 =
63,5 шт.
=
63,5 шт.
5.2.3. Модель экономичного размера партии
Технологический процесс может быть организован на основе производства партии продукции: чередование процессов производства и реализации произведенного:

Рисунок 5.2 - Модель экономичного размера партии
Каким должен быть размер q партии продукции?
Обозначим через Сs стоимость организации производственного цикла (фиксированные издержки производства).
Издержки
ТС = стоимость организации технологического
процесса + хранение =
 (5.3)
(5.3)
где q - экономичный размер партии.
Решение этой задачи:
 .
(5.4)
.
(5.4)
Пример 5.2. Годовой спрос D = 15000 единиц, стоимость организации производственного цикла Сs = 80 рублей, издержки хранения одной единицы Сh = 10 рублей/год.
Экономичный размер партии равен:
=
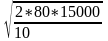 =
490 единиц.
=
490 единиц.
То есть надо произвести 490 единиц, остановить производство, реализовать всю произведенную продукцию и вновь запустить производство. И т. д.
Издержки ТС
равны:
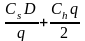 =
=
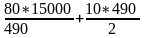 =
4898,98 руб./год.
=
4898,98 руб./год.
Число циклов за год D/q = 15000/490 = 30,6. Расстояние между циклами q/D = 0,03 лет = 12 дней.
