Вычисление объёма тела вращения

Если криволинейная трапеция, ограни­ченная кривой y = f (x), осью Ох и прямыми x = a; x = b, вращается вокруг оси Ох, то объём тела вращения вычисляется по формуле

. (13)

Если фигура, ограни­ченная кривыми y₁ = f₁(x) и y₂ = f₂(x), причём f₁(x) f₂(x), вращается вокруг оси Ох, то объём тела вращения вычисляется по формуле

. (14)

Пример. Найти объём тела, образованного вращением вокруг оси Ох фигуры, ограниченной линиями .

Рис. 8

Решение. По формуле (13), с учётом симметрии кривой относительно оси Ох (рис. 8), получим:

(куб. ед.).

Вычисление площади поверхности вращения

Если дуга гладкой кривой y = f (x) на отрезке [a; b] вращается вокруг оси Ох, то площадь поверхности вращения вычисляется по формуле

. (15)

Если гладкая кривая задана параметрическими уравнениями x = x(t), y = y(t), то площадь поверхности вращения вычисляется по формуле

, (16)

где и определяются из уравнений a = х( ),  b= х( ).

Пример. Найти площадь поверхности, образованной вращением вокруг оси Ох дуги кривой .

Решение. Применим формулу (15). Для этого проведём вспомогательные вычисления:

; ,

получим:

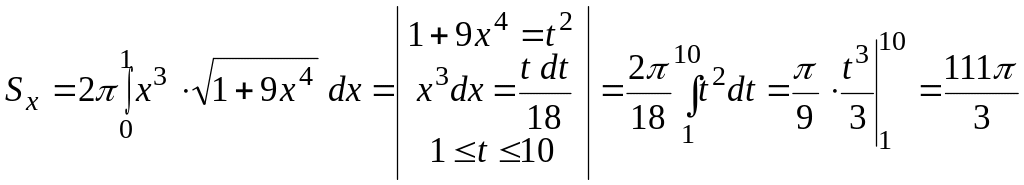(кв. ед.).

Контрольные вопросы:

1. Дайте определение интегральной суммы. Что собой представляет геометрическая интерпретация интегральной суммы?

2. Что называется определенным интегралом? Какова его геометрическая интерпретация? Перечислите основные свойства определенного интеграла.

3. Какие существуют правила вычисления определенных интегралов? Охарактеризуйте каждое их них.

4. Раскройте все возможные случаи применения формул при вычислении площадей плоских фигур.

5. Каким образом вычисляется дуга плоской кривой?

6. Как вычисляется объем тела вращения?

7. Как найти площадь поверхности вращения?

Литература:

1. Высшая математика для экономистов: Учебник для вузов / Н.Ш. Кремер, Б.А. Путко, И.М. Тришин, М.Н.Фридман. Под ред. Н.Ш. Кремера. – М.: ЮНИТИ, 2005. – 471 с.

2. Общий курс высшей математики для экономистов: Учебник. / Под ред. В.И. Ермакова. –М.: ИНФРА-М, 2006. – 655 с.

3. Сборник задач по высшей математике для экономистов: Учебное пособие / Под ред.В.И. Ермакова. М.: ИНФРА-М, 2006. – 574 с.

4. Данко П.Е., Попов А.Г., Кожевникова Т.Я. Высшая математика в упражнениях и задачах. Ч. 1, 2. – М.: Оникс 21 век: Мир и образование, 2005. – 304 с. Ч. 1; – 416 с. Ч. 2.

5. Математика в экономике: Учебник: В 2-х ч. / А.С. Солодовников, В.А. Бабайцев, А.В. Браилов, И.Г. Шандара. – М.: Финансы и статистика, 2006.

6. Шипачев В.С. Высшая математика: Учебник для студ. вузов – М.: Высшая школа, 2007. – 479 с.