Методические указания к проведению лекционного занятия Тема № 4.6. Определенный интеграл

План:

1. Определения и свойства определенного интеграла

2. Правила вычисления определённых интегралов

3. Вычисление площади плоской фигуры

4. Вычисление длины дуги плоской кривой

5. Вычисление объёма тела вращения

6. Вычисление площади поверхности вращения

Определение и свойства определённого интеграла

Пусть функция f (x) определена на отрезке [a; b]. Разделим отрезок [a; b] на n произвольных частей точками

a = x₀ < x₁ < x₂ <  < x_n-1 < x_n = b.

На каждом из полученных отрезков [a; x₁], [x₁; x₂],  , [x_n-1; b] выберем произвольным образом по одной точке:

c₁[a; x₁], c₂[x₁; x₂], . , c_n[x_n-1; b]

и найдём длину каждого такого отрезка:

x₁ = x₁ – a; x₂ = x₂ – x₁;  , x_n = b – x_n-1.

Вычислим значение функции в каждой точке c_i, получим значения

f (c_i), i = 1, 2, . , n.

Рис. 1

Интегральной суммой функции f (x) на отрезке [a; b] называется сумма вида:

. (1)

Каждое слагаемое интеграль­ной суммы представляет собой площадь прямоугольника с высотой f (c_i) и основанием x_i (рис. ).

Обозначим длину наибольшего из отрезков через :

 = max(x_i), i = 1, 2, . , n.

Определенным интегралом от функции на отрезке [a; b] называется предел интегральной суммы (6.1) при условии, что величина  стремится к нулю, а сам предел существует:

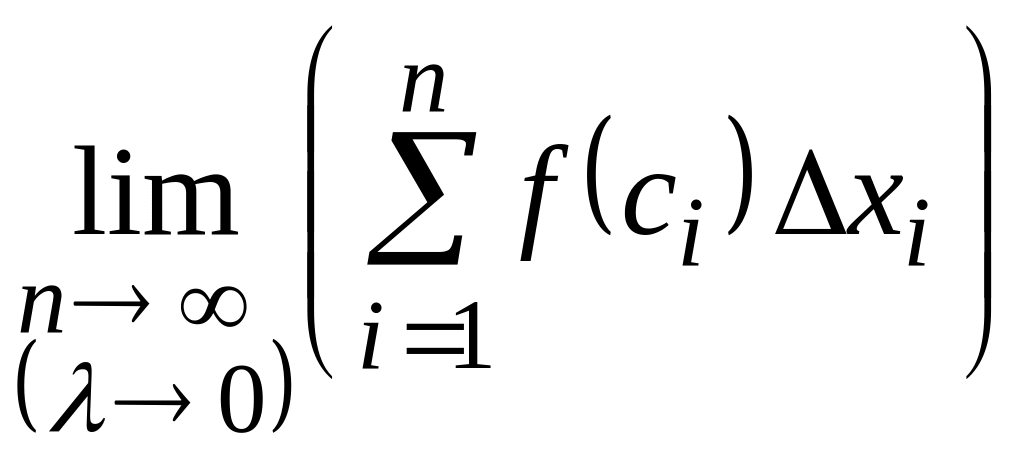= . (2)

Числа a и b в записи определённого интеграла (2) называются соответственно нижним и верхним пределами интегрирования; f(x) называется подынтегральной функцией, f (x)dx – подынтегральным выражением, х - переменной интегрирования.

Теорема (Теорема существования определённого интеграла). Если функция f (x) непрерывна на отрезке [a; b], то предел интегральной суммы (1) не зависит от способа разбиения отрезка [a; b] и от выбора точек c_i.

Рис. 2

Рассмотрим фигуру, ограни­ченную графиком непрерывной, неотрицательной на отрезке [a; b] функции f (x), координатной осью Ох, и прямыми x = a; x = b (рис. 2). Такую фигуру называют криволинейной трапецией, её площадь равна определённому интегралу

.

Если f (x) < 0 во всех точках промежутка [a; b] и непрерывна на этом промежутке, то площадь криволинейной трапеции, ограниченной осью Ох, прямыми x = a; x = b и графиком функции y = f (x), определяется формулой

.

Свойства определенного интеграла

1) , где С ‑ произвольное число;

2) ;

3) ;

4) .

Все приведенные выше свойства непосредственно следуют из определения определенного интеграла.

Правила вычисления определённых интегралов

1. Формула Ньютона-Лейбница:

, (3)

где F(x) - первообразная для функции f(x)

Для того, чтобы вычислить определенный интеграл от функции f(x) на отрезке [a; b], нужно найти какую-либо первообразную F(x) функции f(x) и вычислить разность значений первообразной в точках b и a.

Пример.

2. Формула интегрирования по частям в определённом интеграле:

, (4)

где u = u(x) и v = v(x) — непрерывно дифференцируемые на отрезке [a; b] функции.

Пример. .

3. Формула замены переменной в определенном интеграле:

, (5)

где  и  определяются, соответственно, из уравнений  () = a;  () = b, а функции f, ,  непрерывны на соответствующих промежутках.

При замене переменной в определенном интеграле не нужно возвращаться к исходной переменной интегрирования.

Пример. Вычислить определенный интеграл .

Решение. Выполним замену: ln x = t или x = e^t, тогда если x = 1, то t = 0, а если x = e, то t = 1. В результате получим:

.

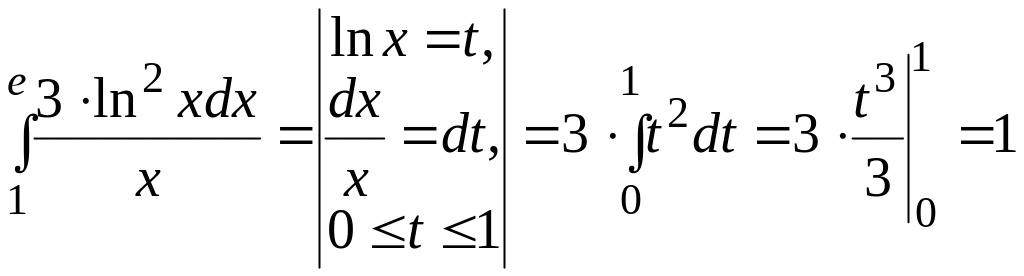Пример. Вычислить определенный интеграл

Решение. Выполним замену переменной: е^х = t, откуда e^xdx = dt, при х = 0 t = 1, при x = t = .