3. Замечательные пределы
Первый
замечательный предел:
.
Доказательство. Рассмотрим единичную окружность (рис.3).
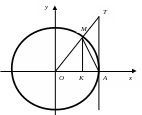
Рис.3. Единичная окружность
Пусть
х
– радианная мера центрального угла МОА
(
),
тогда ОА
= R
=
1, МК
=
sin
x,
AT
= tg
x.
Сравнивая площади треугольников ОМА,
ОТА
и сектора ОМА,
получим:
,
или
,
откуда
.
Разделим последнее неравенство на sin x, получим:
.
Так
как
при
,
то по свойству 5) пределов
при
.
Откуда
и обратная величина
при
,
что и требовалось доказать.
Замечание:
Если функция
является бесконечно малой при
,
т.е.
,
то первый замечательный предел имеет
вид:
.
Рассмотрим примеры вычислений пределов с использованием первого замечательного предела.
1)
.
2)
.
При
вычислении этого предела использовали
тригонометрическую формулу:
.
3)
.
4)
.
Второй
замечательный предел:
,
где e — иррациональное число, приблизительно равное 2,72.
Доказательство. Рассмотрим график функции y = ln x (рис.4).
Рис.4. График функции y = ln x
Проведём
в точке х
= 1 к графику касательную. Её уравнение
имеет вид: у
= х
– 1. Следовательно,
.
Пусть АС = h, тогда ВС = ln(1+ h).
Рассмотрим прямоугольный треугольник АВС.
.
Если
,
то
,
,
т.е.
.
Откуда
при
.
Заменив h
на х,
получим второй замечательный предел,
что и требовалось доказать.
Замечания: 1) Второй замечательный предел можно записать в виде:
.
2) Из второго замечательного предела вытекают следующие пределы:
;
;
;
.
3) Если функция является бесконечно малой при , т.е. , то второй замечательный предел можно записать в виде:
.
Рассмотрим примеры вычислений пределов с использованием второго замечательного предела.
2)
.
3)
.
Имеет место неопределенность типа [1].
Сделаем замену
,
тогда
;
при
.
4. Сравнение бесконечно малых
Пусть
и
являются бесконечно малыми при
,
т.е.
,
.
Рассмотрим предел их отношения:
.
Если А
0,
то
и
являются бесконечно
малыми одного порядка малости
при
.
Если А = 1, то и называют эквивалентными бесконечно малыми при и обозначают
~ при .
Если А = 0, то является бесконечно малой более высокого порядка малости, чем при .
Если предел
не существует, то говорят, что бесконечно
малые
и
несравнимы при
.
Из первого замечательного предела следует, что
х
при
.
Приведём другие примеры эквивалентных функций. Пусть - бесконечно малая при , тогда
-
;
;
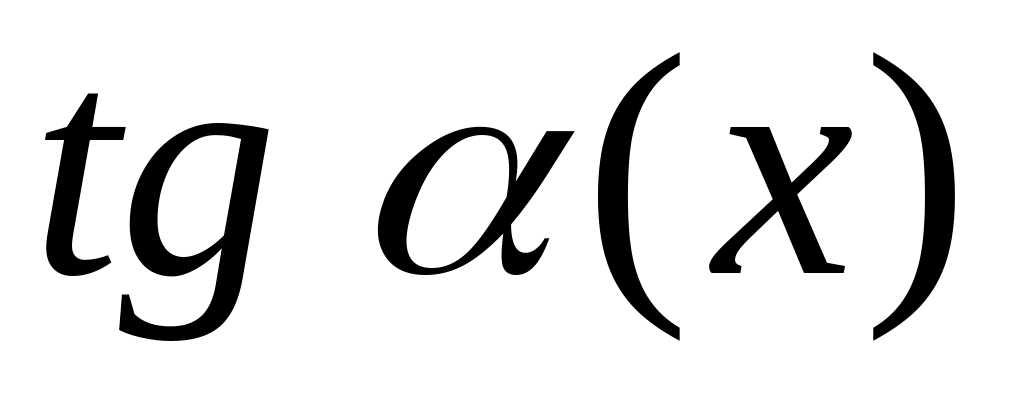
;arctg ;
;1-
;
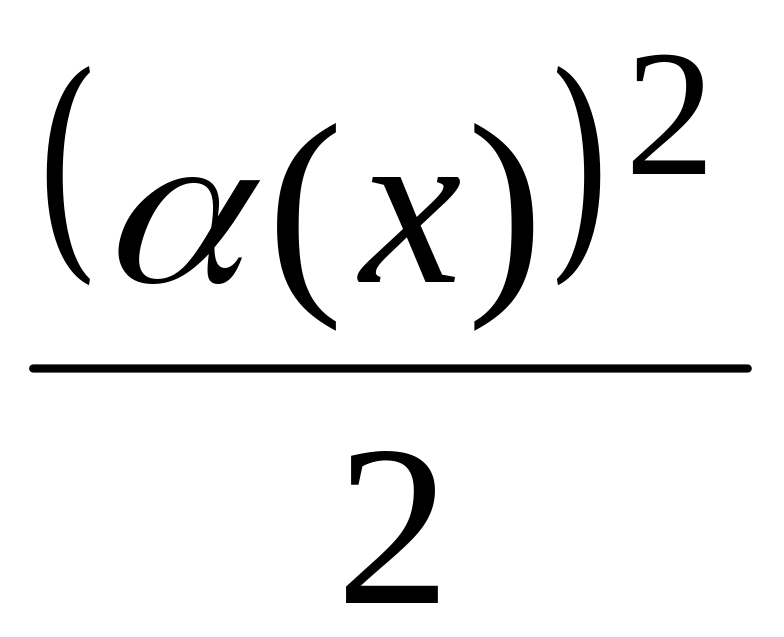ln (1 + ) ;
-
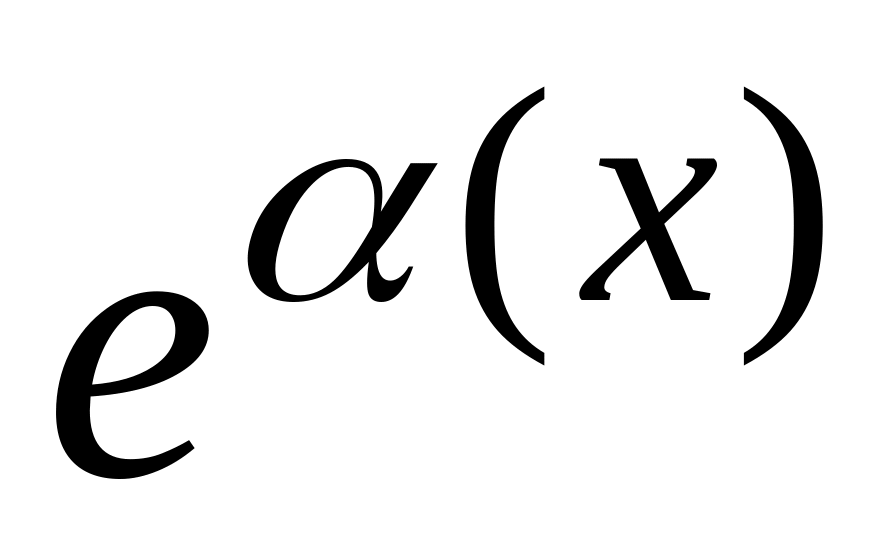1
-
1
;
При вычислении пределов можно заменять бесконечно малые на эквивалентные им.
Примеры:
1)
=
.
В данном пределе неопределённость вида
раскрыта с помощью замены бесконечно
малой функции
на эквивалентную ей бесконечно малую
при
.
2)
=
=
=
=
.
При вычислении предела были использованы
эквивалентности:
;
5х
при
.