Методические указания к проведению лекционного занятия Темы № 2.4. – 2.5. Предел функции. Непрерывность

План:

1. Определение предела функции.

2. Бесконечно малые и бесконечно большие функции.

3. Замечательные пределы.

4. Сравнение бесконечно малых.

5. Непрерывность функции.

6. Классификация точек разрыва.

7. Свойства непрерывных функций.

1. Определение предела функции

Пусть функция определена в некоторой окрестности точки за исключением, быть может, самой точки x₀.

Опр.: Число A называется пределом функции y = f (x) в точке x₀ (или, что тоже самое, при x, стремящемся к x₀), если для любого положительного числа  можно найти такое положительное число , что для всех x из -окрестности точки x₀ соответствующие значения y попадают в -окрестность точки y = A.

Можно сформулировать определение предела функции по-другому.

Опр.: Число A называется пределом функции y = f (x) в точке x₀, если для любого положительного числа  существует такое положительное число , что для всех x, удовлетворяющих неравенству x – x₀  < , выполняется условие y – A < .

Обозначается предел: , или при .

С помощью кванторов всеобщности (для любого) и существования (существует) определение предела функции в точке имеет вид:

.

Геометрический смысл предела функции в точке x₀ заключается в следующем: для любого  > 0 найдётся такая -окрестность точки x₀, что для всех х из этой окрестности соответствующие значения функции y попадают в полосу  - A < y < A +  .

Рис.1. Графическая иллюстрация определения предела функции при

Опр.: Число A называется правым пределом функции y = f (x) в точке x₀, если для любого  > 0 существует такое число  > 0, что для всех x, удовлетворяющих неравенствам x₀ < x <  x₀ + , выполняется условие y – A < . Обозначается:

, или при + 0.

Опр.: Число A называется левым пределом функции y = f (x) в точке x₀, если для любого  > 0 существует такое число  > 0, что для всех x, удовлетворяющих неравенствам x₀ -  < x <  x₀, выполняется условие y – A < . Обозначается: , или при - 0.

Теорема. Функция y = f (x) имеет в точке x₀ предел тогда и только тогда, когда в точке x₀ существуют равные друг другу правый и левый пределы. При этом предел функции равен односторонним пределам.

Свойства пределов:

Пусть функции и имеют конечные пределы в точке x₀, причем , , тогда

1) ;

2) ;

3) , где С – постоянная величина;

4) , если ;

5) если и , то .

Опр.: Число A называется пределом функции y = f (x) при x, стремящемся к бесконечности, если для любого  > 0 существует такое положительное число S, что для всех x, удовлетворяющих условию x  > S, выполняется условие y – A < , т.е.

.

Геометрический смысл предела функции при x, стремящемся к бесконечности: для любого  > 0 найдётся такое число S > 0, что для всех x, удовлетворяющих условию x  > S, соответствующие значения функции y попадают в полосу  - A < y < A +  (рис.).

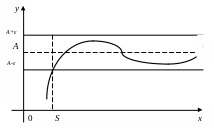
Рис.2. Графическая иллюстрация предела функции при