Методические указания к проведению лекционного занятия Тема № 2.3. Понятие функции, свойства, графики основных элементарных функций.

План:

1. Понятие функции.

2. Способы задания функции.

3. Основные свойства функции.

4. Обратная функция.

5. Сложная функция.

6. Элементарные функции.

1. Понятие функции

При изучении природных и технических процессов сталкиваются с величинами, одни из которых сохраняют одно и то де значение – они называются постоянными, а другие принимают различные числовые значения и называются переменными.

Пример: постоянные величины – температура кипения воды при нормальном давлении, скорость тела, движущегося равномерно и прямолинейно. Скорость камня, брошенного вверх – есть переменная величина – сначала она уменьшается, когда камень достигает наивысшей точки полета – его скорость равна нулю, а затем, под действием силы тяжести скорость снова увеличивается.

Опр.: Переменной величиной называется такая величина, которая при выполнении некоторого комплекса условий, может принимать различные значения.

Опр.: Постоянной величиной называется такая величина, которая при выполнении некоторого комплекса условий, принимает одно и то же значение. Одна и та же величина может быть переменной или постоянной в зависимости от того, в каких условиях она рассматривается.

Переменные величины обычно обозначают последними буквами латинского алфавита: x, y, z, …, а постоянные – первыми: a, b, c, … .

Функция – одно из основных понятий математического анализа, выражающее зависимость одних переменных величин от других.

Опр.: Если каждому значению переменной х, по некоторому правилу или закону ставится в соответствие одно определенное значение переменной у, то говорят, что у – есть однозначная функция от х; обозначается y = f (x).

В уравнении y = f (x) переменную х называют независимой переменной (аргументом), у – зависимой переменной (значением функции). При этом говорят, что величины x и у связаны функциональной зависимостью.

Множество всех значений независимой переменной х, для которых функция y = f (x) определена, называется областью определения функции f и обозначается символом dоm f (от англ. domain - область) или D ( f ).

Множество всех значений функции называется множеством значений или областью изменения функции f и обозначается im f (от англ. image - образ) или Е( f ).

Пример: Найдем область определения функции . Эта функция имеет смысл, если , отсюда или . Следовательно, областью определения этой функции является отрезок , а множеством значений является отрезок .

2. Способы задания функции

Функцию можно задать разными способами, среди которых выделяют аналитический, табличный и графический способы.

Аналитический способ предполагает задание функции с помощью формулы. При этом функция может быть задана:

• в явном виде, т.е. формулой вида y = f (x);

• в неявном виде, т.е. формулой вида F(x, y) = 0;

• параметрически, когда соответствующие друг другу величины x и у выражены через третью переменную величину t, называемую параметром.

Кроме того, функция может быть задана разными формулами на разных промежутках области определения.

Примеры аналитического задания функций:

1) - функция задана явно;

2) - функция задана неявно;

3) - функция задана параметрически;

4)

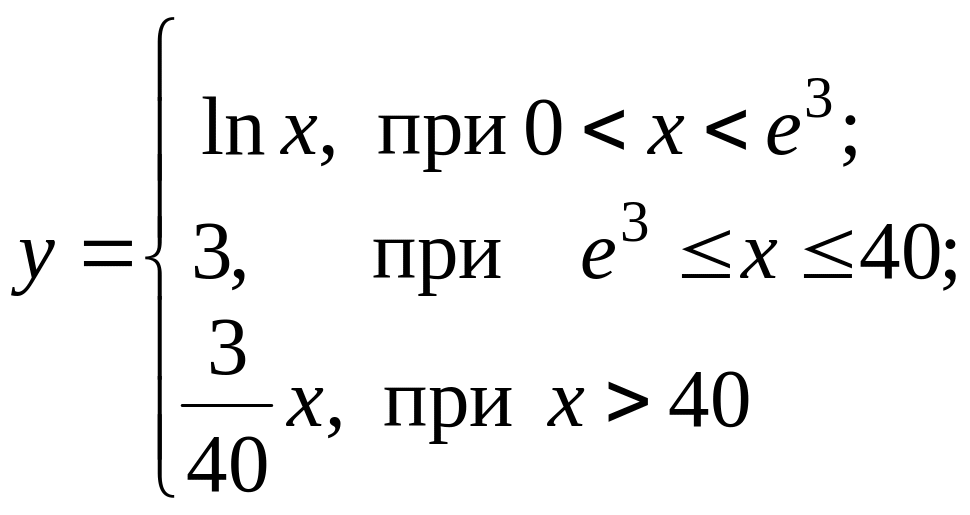
- функция задана разными формулами в области x > 0;

Табличный способ обычно используют в тех случаях, когда область определения функции состоит из конечного числа значений . Значения аргумента записывают в одном столбце, а соответствующие значения функции - в другом.

x			…
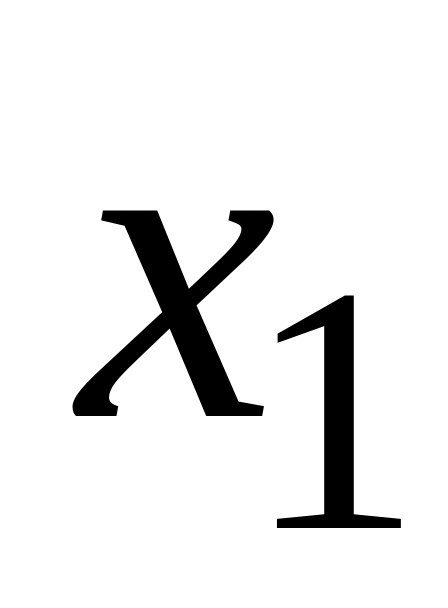
y			…

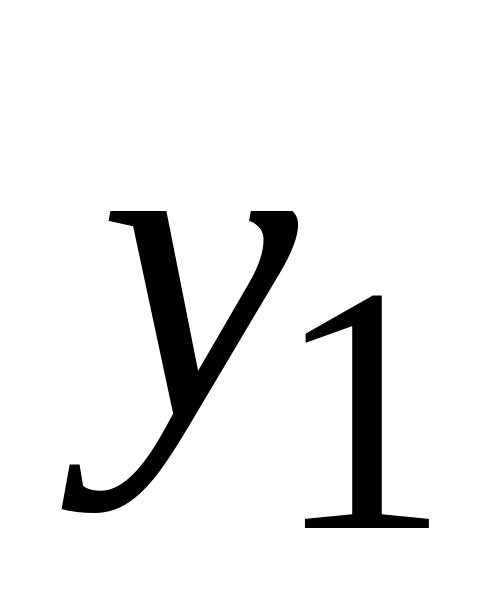
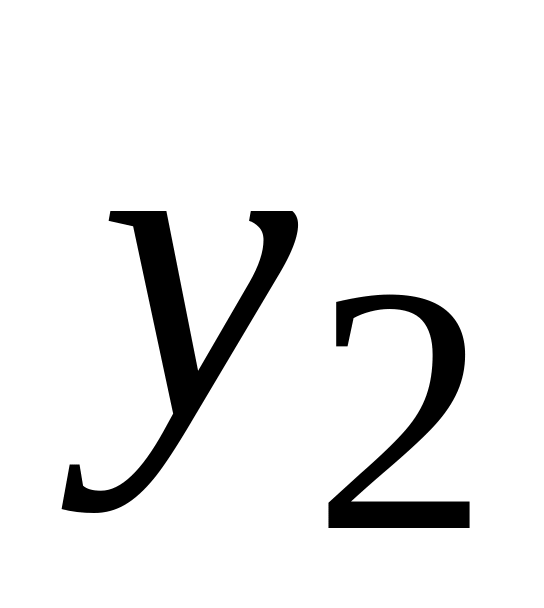
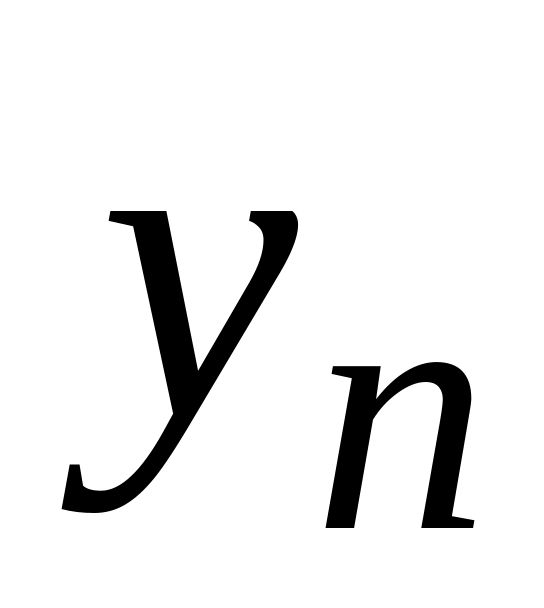
Графический способ предполагает задание функции с помощью графика.

Графиком функции y = f (x) называют множество всех точек плоскости с координатами (x; f (x)), т.е. таких, координаты которых обращают выражение y = f (x) в тождество. На рис. представлен график функции .

Для однозначных функций выполняется следующее свойство: любая прямая, параллельная оси Оу, пересекает график функции либо в одной точке (когда ), либо вовсе не пересекает (когда ).