Направляющие косинусы
Пусть
дан вектор
.
Ортом
вектора
называется единичный вектор
того же направления, что и
.
Вектор можно найти по формуле
(6)
Пусть
вектор
образует с осями координат углы ,
,
.
Косинусы
этих углов
,
,
называются
направляющими
косинусами
вектора
.
Если
,
то направляющие косинусы являются его
координатами:
,
или
, (7)
так как проекции вектора на оси координат имеют вид:
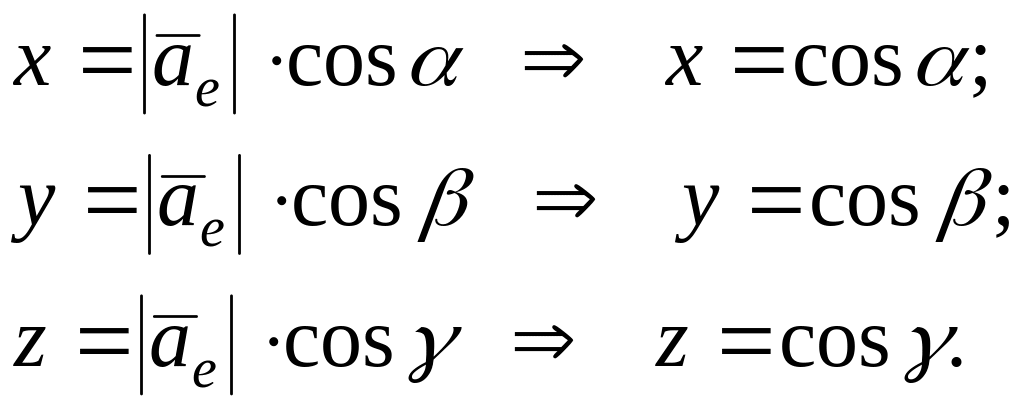
Направляющие косинусы связаны между собой соотношениями:
.
Сравнивая (6) и (7), получим формулы для вычисления направляющих косинусов вектора по его координатам:
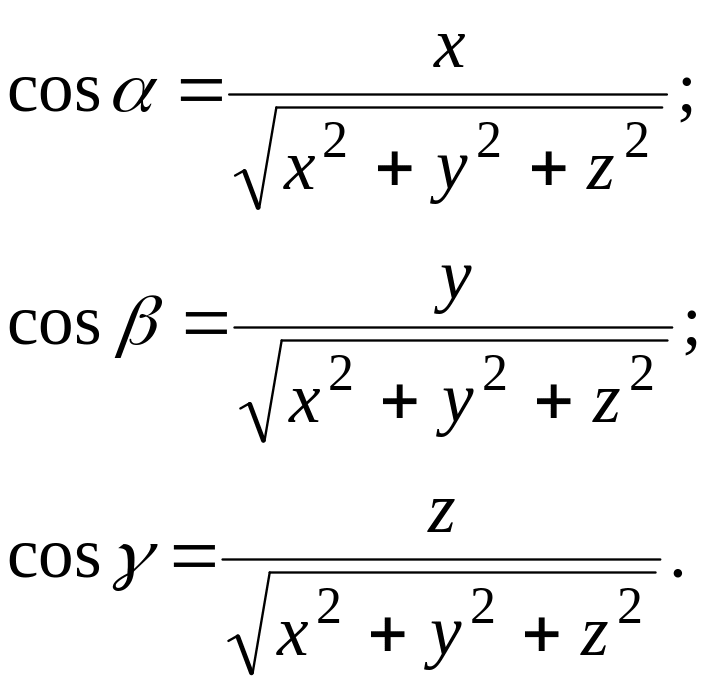(8)
Пример.
Найдите орт вектора
и его направляющие косинусы.
Решение. 1) Найдём длину вектора :
.
2)
По формуле (6)
3)
Направляющие косинусы вектора
– координаты единичного вектора
(см. формулу 8), поэтому
.
Скалярное произведение векторов
Углом
между векторами
и
называют угол между векторами, равными
данным и имеющими общее начало, и
обозначают
,
причем
и
.
Скалярным произведением двух векторов и называется число, равное произведению длин этих векторов на косинус угла между ними:
,
(12)
где – угол между векторами и .
Обозначают скалярное произведение: или ( ).
Так
как 
, то
,
или,
поскольку 
,
то
,
т.е. скалярное произведение векторов равно длине одного вектора, умноженной на проекцию другого на ось, определяемую первым вектором.
Свойства скалярного произведения
1)
.
2)
,
где
– действительное число.
3)
4) Скалярное произведение равно нулю тогда и только тогда, когда его сомножители ортогональны, т.е.
.
5)
,
т.е. скалярный квадрат вектора
равен квадрату его длины, отсюда:
.
Выражение скалярного произведения через координаты
Пусть
даны векторы
и
.
Перемножим их скалярно, используя свойства 2) и 3):
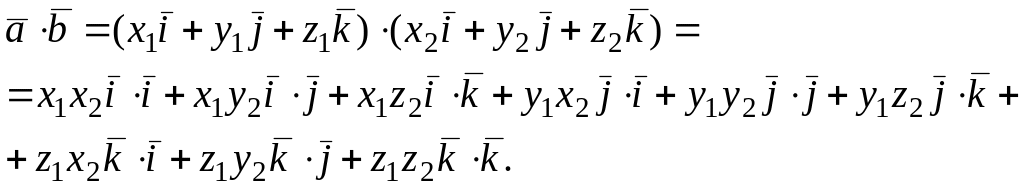
Так
как
;
,
то
.
(13)
Таким образом, скалярное произведение двух векторов, заданных своими координатами, равно сумме произведений одноименных координат.
Из формул (12) и (13) можно получить следующие формулы.
1) Для вектора его модуль вычисляется по формуле
. (14)
2)
Угол между двумя векторами
,
вычисляется по формуле
,
или
. (15)
3) Согласно свойству 4) и формулы (13) условием ортогональности двух векторов и является равенство
.
(16)
4)
Расстояние между точками
и
можно найти как длину вектора
,
т.е.
.
(17)
Пример.
Найдите скалярное произведение векторов
и
.
Решение.
По формуле
(13):
,
т.е.
.
Пример.
Найдите угол
между векторами
и
.
Решение. По формуле (15):
.
Пример.
Вычислите проекцию вектора
на ось, имеющую направление вектора
.
Решение.
Так
как
,
то сначала найдём скалярное произведение
векторов
и
:
,
затем
длину вектора
.
Тогда
.
Здесь отрицательный знак показывает, что угол между вектором и осью проекции – тупой.