Методические указания к проведению лекционного занятия Тема № 1.1. Матрицы и операции над ними

План:

1. Определение матрицы

2. Виды матриц

3. Действия с матрицами

4. Ранг матрицы

5. Собственные значения матрицы

Определение матрицы

Матрицей называется множество чисел, расположенных в виде прямоугольной таблицы из m строк и n столбцов:

. (1)

Числа а_ij, составляющие данную матрицу, называются её элементами. Первый индекс i обозначает номер строки элемента, а второй j - номер столбца. Так, а₂₃ - элемент, стоящий во 2-й строке и 3-м столбце.

Для матрицы (1) используют сокращённую запись:

A = (а_ij) (i = 1, 2, ..., m; j = 1, 2, ... , n),

или

A = А _{m  n} = (а_ij) _{m  n} ,

причём говорят, что матрица А имеет тип m  n ( читается: m на n) или размер m  n.

Заметим, что, во-первых, матрица - это просто условный способ записи чисел в виде прямоугольной таблицы; во-вторых, между числом строк и числом столбцов не требуется никакой зависимости. Матрица может иметь, например, 30 строк и 5 столбцов или 1 строку и 9 столбцов и т.д.

Пример. Из предложенных числовых множеств укажите матрицы:

, , , ,

, , .

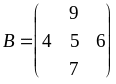Решение. Из заданных числовых множеств матрицами являются только множества A, C, D, F и G. Причём матрица А имеет размер 33, матрица С - 22, матрица D - 31, матрица F - 14 и матрица G - 2 4. Множества В и Е матрицами не являются, поскольку числа в них не записаны в виде прямоугольной таблицы (отсутствуют элементы на пересечении некоторых строк и столбцов).

Виды матриц

Если число строк матрицы (1) не равно числу столбцов ( m  n), то матрица называется прямоугольной.

Из предыдущего примера прямоугольными являются матрицы D, F и G.

В прямоугольной матрице размера m  n:

1) при m = 1 получится матрица-строка:

;

2) при n = 1 получится матрица-столбец:

.

В предыдущем примере матрица F является матрицей-строкой, а матрица D является матрицей-столбцом.

Матрицы-строки и матрицы-столбцы называются матрицами-векто­рами или просто векторами.

Если число строк матрицы (1) равно числу столбцов (m = n), то матрица называется квадратной.

В предыдущем примере квадратными являются матрицы А и С.

Число строк или число столбцов квадратной матрицы называется её порядком.

Так, матрица А имеет 3-й порядок, а матрица С – второй.

Рассмотрим произвольную квадратную матрицу n -го порядка:

Диагональ, содержащая элементы а₁₁ , а₂₂ , ... , а_nn , называется главной, а диагональ, содержащая элементы а_{1 n} , а_{2 n-1} , ... , а_{n 1} , называется побочной.

Квадратная матрица, у которой отличны от нуля только элементы главной диагонали, называется диагональной:

.

Диагональная матрица, у которой все элементы главной диагонали равны 1, называется единичной и обозначается Е:

.

Квадратная матрица, у которой равны нулю только элементы, находящиеся над главной диагональю (или под главной диагональю), называется треугольной:

или .

Прямоугольная матрица называется ступенчатой, если она имеет вид:

,

где a_ii ≠ 0, i = 1, 2, …, r; r < n.

Матрица, все элементы которой равны нулю, называется нулевой и обозначается буквой О:

.

Нулевая матрица может быть любого размера.

Таким образом, матрицы могут быть прямоугольными или квадратными. Прямоугольные матрицы включают в себя ступенчатые матрицы, матрицы-векторы (матрицы-строки и матрицы-столбцы). Квадратные матрицы, в свою очередь, включают диагональные, в том числе единичные, и треугольные. Кроме того, как прямоугольные, так и квадратные матрицы могут быть нулевыми.