
- •6. Ряды динамики
- •6.1. Понятие о рядах динамики
- •6.2. Классификация рядов динамики
- •6.3. Приведение рядов динамики в сопоставимый вид
- •6.4. Определение среднего уровня ряда динамики
- •6.5. Показатели изменения уровней ряда динамики.
- •6.6. Расчет средних абсолютных приростов, темпов роста и темпов прироста
- •6.7. Определение в рядах динамики общей тенденции развития
- •6.8. Определение в рядах внутригодовой динамики
6.4. Определение среднего уровня ряда динамики
В качестве
обобщенной характеристики уровней ряда
динамики служит средний уровень ряда
![]() .
В зависимости от типа ряда динамики
используются различные расчетные
формулы, представленные в таблице 6.7.
.
В зависимости от типа ряда динамики
используются различные расчетные
формулы, представленные в таблице 6.7.
Таблица 6.7.
Вид ряда динамики |
Расчетная формула |
Интервальный ряд абсолютных величин с равными периодами времени |
|
Моментный ряд с равными интервалами между датами |
|
Моментный ряд с неравными интервалами между датами |
|
Пример 6.6.
Данные о выпуске продукции на предприятии представлены интервальным полным рядом динамики:
Год |
1991 |
1992 |
1993 |
1994 |
Выпуск продукции, млн.руб. |
100 |
120 |
150 |
140 |
Средний годовой
выпуск продукции будет получен по
формуле среднего арифметического:
![]()
Пример 6.7.
Остатки материалов на складе на первый день квартала представлены моментным полным рядом динамики:
Квартал |
1 |
2 |
3 |
4 |
Остатки материалов, тыс. руб. |
100 |
120 |
150 |
140 |
Средний остаток материалов на складе на протяжении года определяется по формуле среднего хронологического:
![]()
Пример 6.8.
В списочном составе работников произошли следующие изменения:
по списку на 1.01 числилось 842 человека
выбыло с 5.01 4 человека
принято с 12.01 5 человек
принято с 26.01 2 человека.
Необходимо определить среднюю численность работающих на предприятии в течение января. Исходные данные представляют собой ряд динамики:
Моменты времени |
1.01 |
5.01 |
12.01 |
26.01 |
Численность, человек |
842 |
838 |
843 |
845 |
Расчет численности (средний уровень ряда) осуществляется в таблице 6.8.
Таблица 6.8.
Календарные периоды января |
Число работающих, человек, Хi |
Продолжительность периода, дней, ti |
Проработано человеко-дней, Xiti |
1-4 |
842 |
4 |
3368 |
5-11 |
838 |
7 |
5866 |
12-25 |
843 |
14 |
11802 |
26-31 |
845 |
6 |
5070 |
Всего |
|
31 |
26106 |
Средний уровень ряда динамики определяется по формуле средней арифметической взвешенной: =26106/31=842 человека. В качестве весов ti используются периоды времени, когда уровни ряда не менялись.
6.5. Показатели изменения уровней ряда динамики.
При изучении рядов динамики важно проследить за направлением и размером изменений уровней ряда во времени. С этой целью для динамических рядов рассчитывают следующие показатели:
К - темпы роста;
DY - абсолютные приросты;
DК - темпы прироста;
А - абсолютное значение одного процента прироста.
Темп роста - относительный показатель, получающийся в результате сопоставления двух уровней одного ряда динамики. Темпы роста могут рассчитываться как цепные, когда каждый уровень ряда сопоставляется с предшествующим ему уровнем:
 ,
либо как базисные,
когда все уровни ряда сопоставляются
с одним и тем же уровнем
,
либо как базисные,
когда все уровни ряда сопоставляются
с одним и тем же уровнем
![]() ,
выбранным за базу сравнения :
,
выбранным за базу сравнения :
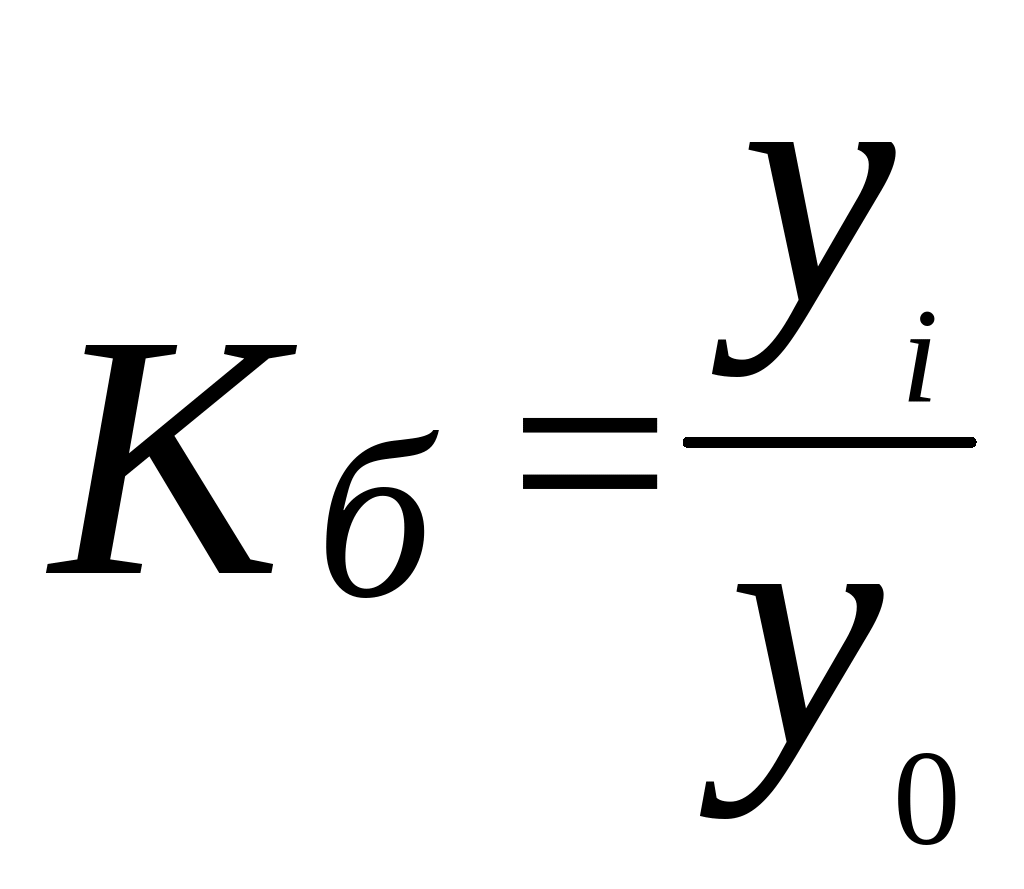
Темпы роста могут быть представлены в виде коэффициентов либо в виде процентов. При расчете процентов расчетные формулы принимают вид:
 - цепные темпы
роста;
- цепные темпы
роста;
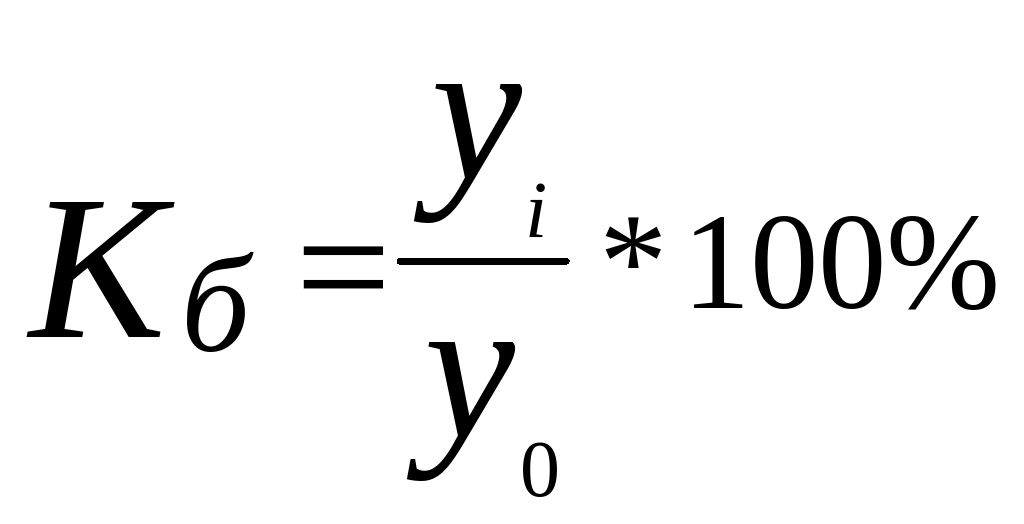 - базисные темпы
роста.
- базисные темпы
роста.
Между цепными и базисными темпами роста существует взаимосвязь - произведение всех цепных темпов роста равно последнему базисному темпу роста:
Абсолютный прирост - разность между двумя уровнями ряда динамики. Абсолютный прирост имеет ту же размерность, что и уровни самого ряда динамики. Абсолютные приросты могут быть и цепными и базисными, в зависимости от способа выбора базы для сравнения:
цепной абсолютный прирост - Dyц = yi - yi-1;
базисный абсолютный прирост - Dyб = yi - y0.
Для относительной оценки абсолютных приростов рассчитываются показатели темпов прироста.
Темп прироста - относительный показатель, показывающий, на сколько процентов один уровень ряда динамики больше (или меньше) другого, принимаемого за базу для сравнения.
![]() - базисные темпы
прироста;
- базисные темпы
прироста;
![]() - цепные темпы
прироста.
- цепные темпы
прироста.
В этих формулах Dyб и Dyц - абсолютный базисный или цепной прирост;
y0 - уровень ряда динамики, выбранный за базу для определения базисных абсолютных приростов;
yi-1 - уровень ряда динамики, выбранный за базу для определения i-го цепного абсолютного прироста.
Существует связь между темпами роста и прироста:
DК = К - 1 или DК = К - 100% (если темпы роста определены в процентах).
Если разделить абсолютный прирост (цепной) на темп прироста (цепной) за соответствующий период, получим показатель, называемый абсолютное значение одного процента прироста: А = Dyц/DКц. Абсолютное значение одного процента прироста равняется одной сотой предыдущего уровня ряда динамики. Увеличение абсолютного значения одного процента прироста свидетельствует о наращивании, интенсификации процесса, изучаемого с помощью ряда динамики.
Пример 6.9.
Выпуск продукции на предприятии описывается рядом динамики:
Год |
1985 |
1986 |
1987 |
1988 |
1989 |
1990 |
Выпуск продукции, млн. руб. |
12.3 |
13.4 |
14.8 |
16.4 |
17.8 |
19.9 |
Необходимо провести анализ динамики выпуска продукции предприятия за 1985-1990 годы.
Темпы роста
Базисные |
Цепные |
К1=13.4/12.3=1.089 |
К1=13.4/12.3=1.089 |
К2=14.8/12.3=1.203 |
К2=14.8/13.4=1.104 |
К3=16.4/12.3=1.333 |
К3=16.4/14.8=1.108 |
К4=17.8/12.3=1.447 |
К4=17.8/16.4=1.085 |
К5=19.9/12.3=1.618 |
К5=19.9/17.8=1.118 |
Абсолютные приросты, млн. рублей.
Базисные |
Цепные |
Dy1=13.4-12.3=1.1 |
Dy1=13.4-12.3=1.1 |
Dy2=14.8-12.3=2.5 |
Dy2=14.8-13.4=1.4 |
Dy3=16.4-12.3=4.1 |
Dy3=16.4-14.8=1.6 |
Dy4=17.8-12.3=5.5 |
Dy4=17.8-16.4=1.4 |
Dy5=19.9-12.3=7.6 |
Dy5=19.9-17.8=2.1 |
Темпы прироста, процентов
Базисные |
Цепные |
DК1=1.1/12.3*100=8.9 |
DК1=1.1/12.3*100=8.9 |
DК2=2.5/12.3*100=20.3 |
DК2=1.4/13.4*100=10.4 |
DК3=4.1/12.3*100=33.3 |
DК3=1.6/14.8*100=10.8 |
DК4=5.5/12.3*100=44.7 |
DК4=1.4/16.4*100=8.5 |
DК5=7.6/12.3*100=61.8 |
DК5=2.1/17.8*100=11.8 |
Вся совокупность показателей ряда динамики, позволяющая посмотреть взаимосвязи между ними, представлена в таблице 6.9. Линии и стрелки в таблице показывают взаимосвязь между различными показателями изменения уровней ряда динамики.

