2. Типология реляционных структур

Ключевые понятия:алгебра, решетка, поле, кольцо, группа, алгебраическая модель, алгебраическая система.

Проведем типологию реляционных структур (см. также пункт 1.2.1). В соответствии с приведённым выше определением реляционной структуры, реляционные структуры можно разбить на два класса:

• неклассические реляционные структуры,

• классические реляционные структуры.

Особый класс реляционных структур – иерархические реляционные структуры.

Среди классических реляционных структур можно проследить следующую типологию:

• алгебраические системы,

• алгебры,

• алгебраическая структура с бинарными операциями (алгебраическая структура, каждая операция которой соответствует некоторому  тернарномуотношению)

• алгебраическая структура с одной бинарной операцией

• группоид

• группоид с нейтральным элементом;

• группоид без нейтрального элемента;

• полугруппа

• коммутативная полугруппа;

• некоммутативная полугруппа;

• полугруппа с правым сокращением;

• полугруппа с двухсторонним сокращением;

• группа

• коммутативная группа (абелева группа);

• алгебраическая структура с двумя бинарными операциями

• кольцо

• тело

• поле;

• решетка

• дедекиндова решетка (модулярная решетка)

• дистрибутивная решетка;

• алгебраические модели

• графовые структуры.

Упражнения к пункту 3.4.2.

Упражнение 3.4.2.24.Является ли алгебраическая система классической реляционной структурой?

Упражнение 3.4.2.25.Могут ли в алгебраической структуре разным отношениям быть сопоставлены алгебраические операции различной арности?

3. Отношения над реляционными структурами. Реляционные метаструктуры

Ключевые понятия и идентификаторы ключевых scb-узлов:реляционная метаструктура,гомоморфизм, изоморфизм, автоморфизм.

Основными отношениями над реляционными структурами являются:

• отношение гомоморфизма,

• отношение изоморфизма,

• отношение автоморфизма (частный вид отношения изоморфизма).

SCBg-текст 3.4.3.. Пример отношения гомоморфизма:

В приведённом примере реляционная структура  Aгомоморфна реляционной структуреBпри соответствии гомоморфизма, заданного отношениемr.

Реляционная структура  Aназывается гомоморфной реляционной структуреB, тогда и только тогда, когда:

1. каждому первичному элементу реляционной структуры   Аоднозначно соответствует первичный элемент структурыB ;

2. каждому сигнатурному множеству реляционной структуры  Аоднозначно соответствует сигнатурное множество структурыB;

3. каждому сигнатурному отношению реляционной структуры  Аоднозначно соответствует сигнатурное отношение структурыB;

4. каждому сигнатурному атрибуту реляционной структуры  Аоднозначно соответствует сигнатурный атрибут структурыB;

5. кроме того: если элемент  e структурыAвключён во множествоsв рамках этой структуры, т. е. существует дуга(   se) , то однозначно соответствующий ему элементe*реляционной структурыB, должен быть включён во множествоs*, включённое в реляционную структуруB, причёмs*– элемент, однозначно соответствующий элементуsв рамках рассматриваемого отношения гомоморфизма, а также дуга(   s*e*)включена в реляционную структуруB и также является элементом, однозначно соответствующим дуге(   se ) в рамках рассматриваемого отношения гомоморфизма.

Реляционные структуры  AиBназываются изоморфными тогда и только тогда, когда реляционная структураAгомоморфна структуреB и реляционная структураB гомоморфна структуреA.

SCBg-текст 3.4.3..Пример отношения изоморфизма

В приведённом примере реляционная структура  Aизоморфна реляционной структуреBпри соответствии изоморфизма, заданного отношениемr .

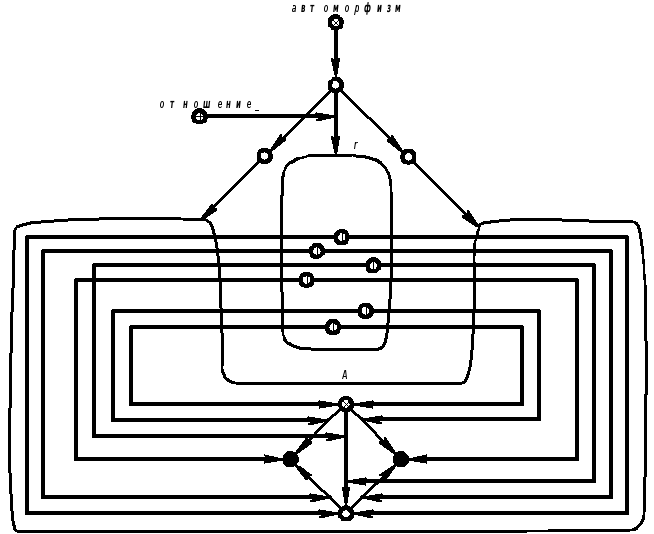
Частным случаем изоморфизма является автоморфизм, когда реляционная структура изоморфна сама себе. Выделив отношения гомоморфизма и изоморфизма, можно перейти к рассмотрению реляционных метаструктур, т.е. таких реляционных структур, в которых вышеперечисленные отношения играют роль сигнатурных, а первичными элементами являются реляционные структуры.

SCBg-текст 3.4.3..Пример отношения автоморфизма

В приведённом примере реляционная структура   Aавтоморфна при соответствии автоморфизма, заданного отношениемr .