Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Московский государственный университет им. М.В. Ломоносова

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Методичка ФЗО общая _последний.doc

Скачиваний:

Добавлен:

01.07.2025

Размер:

2.63 Mб

Скачать

☆

1 / 61 2 3 4 5 6 > Следующая >>>

Министерство Российской Федерации по делам гражданской обороны,

чрезвычайным ситуациям и ликвидации последствий стихийных бедствий

Ивановский институт Государственной противопожарной службы

Кафедра высшей математики и информатики

Е.Г. Родионов, е.В. Старостина, д.С. Фомичёв методические указания к контрольным работам по высшей математике

Для слушателей I курса факультета заочного обучения

Иваново 2008

УДК 51

ББК 22.12

Р 60

Родионов Е.Г. Методические указания к контрольным работам по высшей математике: Учебно-методическое пособие /Е.Г. Родионов, Е.В. Старостина, Д.С. Фомичёв. - Иваново: ООНИ ИвИ ГПС МЧС России, 2008. - 84 с.

Методические указания содержат рекомендации по изучению отдельных разделов курса высшей математики. Весь материал разбит на 6 разделов по количеству контрольных работ. В начале каждой работы содержатся основные теоретические сведения, необходимые для успешного выполнения предложенных контрольных работ. В них также приводятся решения некоторых типовых примеров.

Предназначено для слушателей I курса факультета заочного обучения по специальности 280104.65 «Пожарная безопасность».

Методические указания рассмотрены и рекомендованы к публикации кафедрой высшей математики и информатики. Протокол № 12 от 10.04.2008 г.

Печатается по решению Редакционно-издательского совета Ивановского института государственной противопожарной службы МЧС России.

Рецензенты: Т.М. Лопатина - доцент кафедры высшей математики Ивановского государственного энергетического университета, к.ф.-м.н.

В.А. Комельков - преподаватель кафедры пожарной автоматики Ивановского института ГПС МЧС России, к.т.н.

 ИвИ ГПС МЧС России, 2008

Оглавление

Предисловие . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 4

Методические указания к контрольным работам . . . . . . . . . 10

Контрольная работа №1. Элементы линейной алгебры и

аналитической геометрии. Комплексные числа . . . . . . . . . . 10

Контрольная работа №2. Введение в математический

анализ. Дифференциальное исчисление функций одной

переменной . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 29

Контрольная работа №3. Исследование функций с по-

мощью производных. Интегральное исчисление функций

одной переменной . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 39

Контрольная работа №4. Функции нескольких перемен-

ных. Кратные и криволинейные интегралы . . . . . . . . . . . . . 50

Контрольная работа №5. Ряды. Обыкновенные диф-

ференциальные уравнения . . . . . . . . . . . . . . . . . . . . . . . . . . . 59

Контрольная работа №6. Основы теории вероятностей . . . 69

Список рекомендуемой литературы . . . . . . . . . . . . . . . . . . . . . . . . 83

ПРЕДИСЛОВИЕ

Основная цель настоящих методических указаний – способствовать развитию практических навыков у слушателей при самостоятельной работе над учебным материалом.

Пособие предназначено для слушателей 1 курса факультета заочного обучения ИвИ ГПС МЧС России, содержит рекомендации по решению задач контрольных работ №№ 1, 2 ,3, 4, 5, 6.

Тема контрольной работы №1 «Элементы линейной алгебры и аналитической геометрии. Комплексные числа».

Тема контрольной работы №2 «Введение в математический анализ. Дифференциальное исчисление функций одной переменной».

Тема контрольной работы №3 «Исследование функций с помощью производных. Интегральное исчисление функций одной переменной».

Тема контрольной работы №4 «Функции нескольких переменных. Кратные и криволинейные интегралы».

Тема контрольной работы №5 «Ряды. Обыкновенные дифференциальные уравнения».

Тема контрольной работы №6 «Основы теории вероятностей».

В начале каждой работы содержатся основные теоретические сведения, необходимые для успешного выполнения предложенных контрольных работ. Также приводятся решения некоторых типовых примеров.

Изучая литературу, особое внимание следует обратить на теоретические вопросы, публикуемые ниже. Они входят в программу экзамена и зачетного собеседования.

Основные требования, с которыми Вам придется столкнуться на экзамене:

Умение четко сформулировать каждое понятие, истолковать его геометрический или физический смысл, приводить примеры, иллюстрирующие понятие.
Умение четко формулировать и доказывать теоремы, знать выводы формул, указанных в вопросах.
Знание основных формул и приемов, умение применять их к решению задач.

Теоретические вопросы

Определители 2 и 3 порядка, свойства определителей.
Матрицы, виды матриц. Действия с матрицами. Обратная матрица.
Система линейных уравнений (основные понятия). Матричный способ решения систем линейных уравнений. Формулы Крамера.
Векторное произведение и его свойства. Векторное произведение в координатах. Приложения векторного произведения.
Смешанное произведение и его свойства. Смешанное произведение в координатах. Приложения смешанного произведения.
Векторы. Линейные операции над векторами. Разложение векторов по базису. Скалярное произведение векторов.
Координаты вектора. Действия над векторами в координатах. Угол между векторами. Направляющие косинусы.
Виды уравнения прямой на плоскости.
Угол между прямыми. Условия параллельности и перпендикулярности прямых. Расстояние от точки до прямой.
Уравнение плоскости с нормальным вектором. Общее уравнение плоскости.
Угол между плоскостями. Условия параллельности и перпендикулярности плоскостей. Расстояние от точки до плоскости.
Прямая в пространстве. Каноническое уравнение прямой в пространстве. Параметрическое уравнение прямой.
Кривые второго порядка. Окружность.
Эллипс. Исследование канонического уравнения эллипса.
Гипербола. Исследование уравнения гиперболы.
Канонические уравнения параболы и их исследования.
Комплексные числа в алгебраической форме и действия с ними.
Геометрическая интерпретация комплексного числа. Тригонометрическая и показательная формы комплексного числа.
Действия с комплексными числами в тригонометрической и показательной формах.
Предел функции в точке. Односторонние пределы. Предел функции при . Теоремы о пределах функции.
Первый и второй замечательные пределы.
Бесконечно малые и бесконечно большие функции. Эквивалентные бесконечно малые и их свойства.
Непрерывные функции и их свойства.
Точки разрыва и их классификация.
Производная функции, ее механический и геометрический смысл. Производные основных элементарных функций.
Производная суммы, разности, произведения, частного функций. Производная сложной функции.
Производная неявно и параметрически заданной функции, логарифмическое дифференцирование.
Дифференциал функции и его геометрический смысл. Применение дифференциала к приближенным вычислениям.
Правило Лопиталя, раскрытие неопределенностей.
Производные высших порядков (явно, неявно и параметрически заданных функций).
Монотонность и экстремумы функции.
Выпуклость графика функции и точки перегиба.
Асимптоты графика функции.
Понятие функции нескольких переменных. Изображение функции двух переменных в пространстве. Линии уровня.
Частные производные функции двух переменных.
Полный дифференциал функции нескольких переменных, связь его с частными производными.
Касательная плоскость и нормаль к поверхности.
Производная по направлению. Градиент функции .
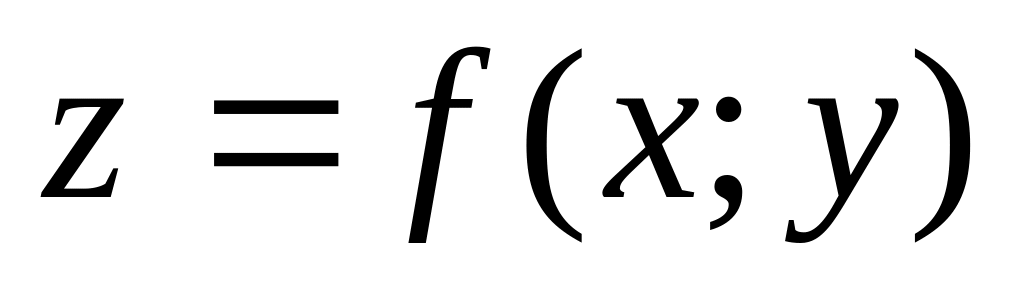Экстремумы функций двух переменных (основные понятия, необходимые условия экстремума, достаточные условия экстремума).
Условный экстремум. Метод множителей Лагранжа.
Понятия первообразной и неопределённого интеграла. Таблица основных неопределённых интегралов. Свойства неопределённого интеграла. Методы интегрирования: непосредственное интегрирование, метод подстановки.
Дробно-рациональная функция и её представление в виде суммы простейших дробей. Интегрирование простейших рациональных дробей. Интегрирование дробно-рациональных функций.
Универсальная тригонометрическая подстановка. Интегралы типа . Использование тригонометрических преобразований.
Интегрирование простейших иррациональностей. Квадратичные иррациональности. Дробно-линейная подстановка. Тригонометрическая подстановка.
Понятие определённого интеграла. Формула Ньютона-Лейбница. Свойства определённого интеграла. Методы вычисления определённого интеграла.
Геометрический смысл определённого интеграла. Вычисления площадей плоских фигур: в прямоугольных координатах, в полярных координатах.
Несобственные интегралы первого рода (с бесконечным промежутком интегрирования). Признаки сравнения. Абсолютная сходимость.
Несобственные интегралы второго рода (от разрывной функции). Признаки сходимости.
Задачи, приводящие к дифференциальным уравнениям. Основные понятия теории дифференциальных уравнений. Дифференциальные уравнения 1^го порядка с разделяющимися переменными.
Дифференциальные уравнения 1^го порядка: однородные, линейные и уравнения в полных дифференциалах.
Дифференциальные уравнения высших порядков. Основные понятия. Уравнения, допускающие понижение порядка.
Линейные дифференциальные уравнения n–го порядка. Линейные однородные дифференциальные уравнения 2–го порядка и свойства его решения. Линейные однородные дифференциальные уравнения n–го порядка.
Линейные однородные дифференциальные уравнения 2–го порядка с постоянными коэффициентами. Линейные однородные дифференциальные уравнения n–го порядка с постоянными коэффициентами.
Неоднородные линейные дифференциальные уравнения 2–го порядка. Структура общего решения. Метод нахождения частных решений (метод вариации постоянных).
Неоднородные линейные дифференциальные уравнения 2–го порядка с постоянными коэффициентами и с правой частью специального вида.
Двойной интеграл. Определение. Геометрический смысл. Основные свойства.
Вычисление двойного интеграла в декартовой системе координат (случай прямоугольной и криволинейной областей). Вычисление площади плоской фигуры.
Замена переменной в двойном интеграле. Вычисление двойных интегралов в полярной системе координат.
Тройной интеграл. Определение. Основные свойства тройного интеграла.
Вычисление тройного интеграла в декартовых координатах. Вычисление объема тела.
Замена переменной в тройном интеграле. Вычисление тройных интегралов в цилиндрических и сферических координатах.
Криволинейные интегралы 1 рода.
Криволинейные интегралы 2 рода.
Поверхностные интегралы 1 рода.
Поверхностные интегралы 2 рода.
Векторное поле.
Числовые ряды. Основные понятия. Свойства. Необходимый признак сходимости.
Достаточные признаки сходимости знакопостоянных рядов.
Знакочередующиеся ряды. Признак Лейбница.
Абсолютная и условная сходимости числовых рядов. Свойства абсолютно сходящегося ряда.
Степенные ряды. Основные понятия. Теорема Абеля.
Интервал и радиус сходимости степенного ряда. Свойства степенных рядов.
Ряды Тейлора и Маклорена. Теорема о единственности разложения функции в степенной ряд.
Понятие тригонометрического ряда Фурье. Вывод формул для коэффициентов Фурье. Формулировка теоремы Дирихле.
Разложение в ряд Фурье четных и нечетных функций заданных на отрезке [-П; П]. Разложение в ряд Фурье функций произвольного периода.
Основные понятия комбинаторики (размещения, сочетания, перестановки). Примеры.
Случайные события, его виды. Классическое и статистическое определение вероятности. Примеры.
Теорема сложения вероятностей несовместных и совместных событий.
Теорема умножения вероятностей независимых и зависимых событий.
Формулы полной вероятности и Байеса.
Закон распределения дискретной случайной величины. Биномиальное распределение и распределение Пуассона.
Функция и плотность распределения. Равномерное распределение непрерывной случайной величины.
Математическое ожидание дискретной и непрерывной случайной величины. Свойства математического ожидания.
Дисперсия дискретной и непрерывной случайной величины. Свойства дисперсии.
Статистика и ее задачи. Основы обработки статистических данных. Вариационные ряды и их графическое изображение. Основы выборочного метода. Генеральная совокупность и выборка. Среднее квадратическое отклонение.
Проверка статистических гипотез. Критерии согласия.
Простейший поток событий. Математическое моделирование потока вызовов пожарных подразделений.

МЕТОДИЧЕСКИЕ УКАЗАНИЯ

К КОНТРОЛЬНЫМ РАБОТАМ

КОНТРОЛЬНАЯ РАБОТА №1

ЭЛЕМЕНТЫ ЛИНЕЙНОЙ АЛГЕБРЫ И

АНАЛИТИЧЕСКОЙ ГЕОМЕТРИИ. КОМПЛЕКСНЫЕ ЧИСЛА

Основные теоретические сведения

1. Определителем (детерминантом) -го порядка называется число , равное алгебраической сумме членов, составленных определенным образом из элементов определителя. Обозначение:

Алгебраическим дополнением элемента определителя -го порядка называется определитель -го порядка, полученный из исходного вычеркиванием -й строки и -го столбца и умноженный на .

Рекуррентная формула для вычисления определителя -го порядка имеет вид

(разложение определителя по элементам -й строки).

Определитель второго порядка

2. Скалярным произведением двух векторов и называется число, определяемое равенством

, (1)

где - угол между векторами и .

3. Векторным произведением двух векторов и называется вектор , длина которого равна произведению длин векторов-сомножителей на синус угла между ними и который направлен перпендикулярно векторам и так, что векторы , , , образуют правую тройку (рис.1):

(2)

Геометрически равен площади параллелограмма, построенного на векторах и :

Рис.1 Рис.2

4. Смешанное произведение трех векторов , , есть число, равное

(3)

Модуль смешанного произведения равен объему параллелепипеда, построенного на векторах , , .

5. Общее уравнение плоскости имеет вид

где - нормальный вектор плоскости (рис.2).

Уравнение плоскости, проходящей через три заданные точки , и , имеет вид

. (4)

Угол между двумя плоскостями, имеющими нормальные векторы и , определяется как угол между и ; косинус этого угла находится по формуле

. (5)

6. Уравнения прямой в пространстве, проходящей через две заданные точки и , имеют вид

(6)

7. Матрицей размера называется прямоугольная таблица чисел, состоящая из строк и столбцов:

Произведением матрицы размера на матрицу размера называется матрица размера с элементами

(7)

(поэлементное умножение -й строки матрицы на -й столбец матрицы ).

Матрица размера называется квадратной матрицей -го порядка. Элементы образуют главную диагональ матрицы. Определитель, составленный из элементов квадратной матрицы, называется определителем матрицы и обозначается или .

Матрица с элементами называется единичной матрицей -го порядка.

Матрица называется обратной к матрице ( ), если

. (8)

Элементы обратной матрицы вычисляются по формулам

(9)

где - алгебраическое дополнение элемента матрицы , а - ее определитель.

8. Система трех линейных уравнений с тремя неизвестными , , имеет вид

(10)

где - коэффициенты системы; - свободные члены. Определитель третьего порядка , составленный из коэффициентов при неизвестных, называется определителем системы. Если , то единственное решение системы (10) выражается формулами Крамера:

(11)

где - определители третьего порядка, получаемые из определителя системы заменой 1, 2 или 3-го столбца соответственно свободными членами

Систему (10) можно записать в матричной форме: ,

где , , .

Тогда ее решение имеет вид

, (12)

если определитель системы отличен от нуля.

9. Кривые второго порядка: кривые, описываемые уравнениями вида:

. (13)

Окружностью (рис.3) называется множество всех точек плоскости, равноудаленных от данной точки, называемой центром окружности.

Рис.3

Каноническое уравнение окружности:

, (14)

где т. – центр окружности, – радиус окружности.

Рис.4

Эллипсом (рис.4) называется множество всех точек плоскости, сумма расстояний от каждой из которых до двух данных точек этой плоскости, называемых фокусами, есть величина постоянная, большая, чем расстояние между фокусами.

Каноническое уравнение эллипса:

. (15)

– фокусное расстояние;

– большая полуось; – малая полуось => .

Эксцентриситет эллипса: ; .

Рис.5

Гиперболой (рис.5) называется множество всех точек плоскости, модуль разности расстояний от каждой из которых до двух данных точек этой плоскости, называемых фокусами, есть величина постоянная, меньшая, чем расстояние между фокусами.

Каноническое уравнение гиперболы:

. (16)

и – вершины гиперболы;

– действительная полуось; – мнимая полуось => .

Асимптоты гиперболы: .

Эксцентриситет гиперболы: .

Рис.6

Параболой (рис.6) называется множество всех точек плоскости, каждая из которых одинаково удалена от данной точки, называемой фокусом, и данной прямой, называемой директрисой.

Расстояние от фокуса до директрисы называется параметром параболы и обозначается через .

Каноническое уравнение параболы:

. (17)

Директриса параболы: .

10. Выражение вида называется комплексным числом (в алгебраической и тригонометрической форме соответственно). Здесь , - действительная часть, а - мнимая часть комплексного числа ; и - модуль и аргумент числа :

, ( ). (18)

Комплексное число изображается на координатной плоскости точкой или вектором , начало которого совпадает с началом координат, а конец – с точкой (рис.7).

Аргумент комплексного числа можно находить так:

найти острый угол ;
если четверти, то ;

если четверти, то ;

е сли четверти, то .

Рис.7

Возведение в натуральную степень числа производится по формуле

, (19)

которая называется формулой Муавра.

Извлечение корня -й степени ( - натуральное число) из числа ( ) производится по формуле

, (20)

где - арифметический корень из модуля , а 0, 1,…, .

Пример 1. По координатам вершин пирамиды , , , найти: 1) длины ребер и ; 2) угол между ребрами и ; 3) площадь грани ; 4) объем пирамиды .

Решение: 1) Находим векторы и :

;

Длины этих векторов, т.е. длины ребер и , таковы:

;

2) Скалярное произведение векторов и находим по формуле (1):

а косинус угла между ними – по формуле (5):

Отсюда следует, что - тупой угол, равный . Это и есть искомый угол между ребрами и .

3) Площадь грани равна половине площади параллелограмма, построенного на векторах и , т.е. половине модуля векторного произведения этих векторов [см. формулу (2)]:

Здесь определитель вычисляется с помощью разложения по первой строке. Следовательно,

4) Объем пирамиды равен объема параллелепипеда, построенного на векторах , , . Вектор Используя формулу (3), получаем

Пример 2. Найти угол между плоскостью , проходящей через точки , , , и плоскостью , заданной уравнением .

Решение: Уравнение плоскости находим по формуле (4):

, ,

т. е.

По уравнениям плоскостей определяем их нормальные векторы: , . Угол между плоскостями и находим по формуле (5):

откуда .

Пример 3. Составить уравнение прямой, проходящей через точки и .

Решение: Используя формулу (6), получаем

Равенство нулю знаменателя второй дроби означает, что прямая принадлежит плоскости

Пример 4. С помощью формул Крамера найти решение системы линейных уравнений

(21)

Решение: Вычислим определитель системы

Так как , то решение системы может быть найдено по формулам Крамера (11). Для этого найдем :

, ,

Подставляя найденные значения определителей в формулы (11), получаем искомое решение системы: , , .

Пример 5. Найти решение системы примера 4 с помощью обратной матрицы.

Решение: Здесь , , .

Так как определитель матрицы системы отличен от нуля (см. пример 4): , то матрица имеет обратную. Для нахождения обратной матрицы вычислим алгебраические дополнения элементов матрицы :

, , ,

, , .

Согласно формуле (9), матрица , обратная к , имеет вид

Матричное решение системы (21) в силу формулы (12) имеет вид

откуда следует (из условия равенства двух матриц), что , , .

Пример 6. Даны координаты вершин треугольника АВС: А(-1;2), В(5;-1), С(-4;-5). Найти: 1) уравнение медианы АЕ; 2) уравнение и длину высоты СD; 3) уравнение прямой, проходящей через точку Е параллельно стороне АВ.

Решение: 1) Для составления уравнения медианы АЕ найдем сначала координаты точки Е, которая лежит на середине отрезка ВС:

Уравнение прямой, проходящей через две заданные точки плоскости А(x₁;y₁) и В(x₂;y₂), имеет вид

(22)

Теперь, подставив в (22) координаты точек А и Е, получаем уравнение медианы:

(АЕ).

2) Для составления уравнения высоты СD воспользуемся уравнением прямой, проходящей через заданную точку М₀(x₀;y₀) с заданным угловым коэффициентом , которое имеет вид

, (23)

и условием перпендикулярности прямых АВ и СD, которое выражается соотношением , откуда . Подставив в (23) вместо значение , а вместо x₀, y₀ координаты точки С, получим уравнение высоты СD:

(CD).

Для вычисления длины высоты CD воспользуемся формулой отыскания расстояния от заданной точки М₀(x₀;y₀) до заданной прямой с уравнением , которая имеет вид

(24)

Подставив в (24) вместо x₀, y₀ координаты точки С, а вместо А, В и С коэффициенты уравнения прямой АВ, получаем

3) Так как искомая прямая ЕF параллельна прямой АВ, то Подставив в уравнение (23) вместо x₀, y₀ координаты точки Е, а вместо значение , получаем уравнение прямой ЕF:

(ЕF).

Пример 7. Составить уравнение гиперболы, проходящей через точку , если асимптоты гиперболы имеют уравнения .

Решение:

Уравнение асимптот: => => .

Подставим данные в уравнение гиперболы (16):

=> => => => => => .

Уравнение гиперболы: .

Пример 8. Записать число в тригонометрической форме.

Решение: Находим модуль

Находим угол

Рис.8

Вектор, соответствующий данному комплексному числу, лежит в III координатной четверти (рис.8), поэтому одним из аргументов является Следовательно,

Это и есть тригонометрическая форма комплексного числа .

Пример 9. Записать число в алгебраической форме.

Решение: Сначала найдем и :

Тогда , Следовательно,

Пример 10. Вычислить

Решение: Запишем сначала число в тригонометрической форме: (см. пример 9). Теперь воспользуемся формулой Муавра (19). Тогда

КОНТРОЛЬНАЯ РАБОТА №2

ВВЕДЕНИЕ В МАТЕМАТИЧЕСКИЙ АНАЛИЗ.

ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ ФУНКЦИЙ

ОДНОЙ ПЕРЕМЕННОЙ

Основные теоретические сведения

1. Определение конечного предела функции в точке: число называется пределом функции при , если для любого найдется такое, что при . Обозначение: или при .

Функция ( ) называется бесконечно малой (бесконечно большой) при , если ( ).

Две функции и , одновременно стремящиеся к нулю или бесконечности при , называются эквивалентными, если . Обозначение: .

Предел отношения бесконечно малых (бесконечно больших) функций не изменится, если каждую из них заменить эквивалентной ей функцией, т.е.

, (1)

если , .

2. К основным элементарным функциям относятся: 1) степенная функция ; 2) показательная функция ; 3) логарифмическая функция ; 4) тригонометрические функции: ,

, , ; 5) обратные тригонометрические функции: , , , .

Предел элементарной функции в точке области ее определения равен частному значению функции в этой точке: .

Нарушение ограничений, накладываемых на функции при вычислении их пределов, приводит к неопределенностям вида

, , , , , , .

Элементарными приемами раскрытия неопределенностей являются:

сокращение на множитель, создающий неопределенность;
деление числителя и знаменателя на старшую степень аргумента (для отношения многочленов при );
применение эквивалентных бесконечно малых и бесконечно больших;
использование первого замечательного предела:

; (2)

использование второго замечательного предела:

. (3)

Отметим также, что

, если ;

, если , ;

, если , .

3. Функция называется непрерывной в точке , если:

частное значение функции в точке равно ;
существуют конечные односторонние пределы функции

, ; (4)

односторонние пределы равны:

; (5)

предельное значение функции в точке равно ее частному значению :

. (6)

Обозначение: .

Точка называется точкой устранимого разрыва, если [нарушается условие (6)].

Точка называется точкой разрыва первого рода, если оба односторонних предела конечны, но [нарушается условие (5)].

Точка называется точкой разрыва второго рода, если хотя бы один из односторонних пределов равен бесконечности или не существует [нарушается условие (4)].

4. Производной функции в точке называется предел отношения приращения функции к приращению аргумента, когда приращение аргумента стремится к нулю:

(7)

или

. (8)

Функция , имеющая производную в каждой точке интервала , называется дифференцируемой в этом интервале; операция нахождения производной функции называется дифференцированием.

Обозначение: , .

5. Физический смысл производной: Если функция описывает какой-либо физический процесс, то производная есть скорость протекания этого процесса.

6. Геометрический смысл производной: Производная в точке x равна угловому коэффициенту касательной к графику функции в точке, абсцисса которой равна x.

7. Уравнение касательной в точке :

. (9)

8. Уравнение нормали в точке :

, если . (10)

9. Теорема о непрерывности: Если функция дифференцируема в некоторой точке, то она непрерывна в ней.

10. Правила дифференцирования:

, где .
.
.
, где .
, .

11. Производная сложной и обратной функции:

Пусть и , тогда – сложная функция с промежуточным аргументом и независимым аргументом x.

Теорема: Если функция имеет производную в точке x, а функция имеет производную в соответствующей точке , то сложная функция имеет производную в точке x, которая находится по формуле .

Таким образом, для нахождения производной сложной функции надо производную данной функции по промежуточному аргументу умножить на производную промежуточного аргумента по независимому аргументу.

Пусть и – взаимно обратные функции.

Теорема: Если функция строго монотонна на интервале и имеет неравную нулю производную в произвольной точке этого интервала, то обратная ей функция также имеет производную в соответствующей точке, определяемую равенством или .

Таким образом, производная обратной функции равна обратной величине производной данной функции: .

12. Производные основных элементарных функций:

1. Степенная функция : .

2. Показательная функция: : .

3. Логарифмическая функция: : . В частности, .

4. Тригонометрические функции: ; ; ; .

; ;

; .

5. Обратные тригонометрические функции: ; ; ; .

; ;

; .

13. Правило Лопиталя. Предел отношения двух бесконечно малых или бесконечно больших функций (неопределенность или ) равен пределу отношения их производных:

, (11)

если предел справа существует.

Пример 1. Найти

Решение: Подставляя вместо его предельное значение, равное 3, получаем в числителе бесконечно большую, а в знаменателе – бесконечно малую функцию:

Поэтому

Пример 2. Найти

Решение: Подстановка предельного значения аргумента приводит к неопределённости вида . Так как под знаком предела стоит отношение двух многочленов, то разделим числитель и знаменатель на старшую степень аргумента, т. е. на В результате получим

поскольку при функции и являются бесконечно малыми.

Пример 3. Найти

Решение: Для раскрытия получающейся здесь неопределенности вида используем метод замены бесконечно малых эквивалентными. Так

как при то на основании формулы (1) находим

Пример 4. Найти

Решение: Подстановка приводит к неопределенности . Произведем замену переменных: , Тогда

Здесь использован второй замечательный предел (3).

Пример 5. Исследовать функцию

на непрерывность; найти точки разрыва функции и определить их тип. Построить схематический график функции.

Решение: Так как данная функция определена на всей числовой оси, то «подозрительными на разрыв» являются те точки, в которых изменяется аналитическое выражение функции, т. е. точки и . Вычислим односторонние пределы в этих точках.

Для точки имеем:

Односторонние пределы функции в точке существуют, но не равны между собой. Следовательно, эта точка является точкой разрыва первого рода.

Для точки получаем

Односторонние пределы функции при равны между собой и равны частному значению функции: Следовательно, исследуемая точка является точкой непрерывности. График данной функции приведен на рис.9.

Рис.9

Пример 6. Используя правило Лопиталя, вычислить предел функций:

1) 2)

Решение: 1) Подстановка предельного значения аргумента приводит к неопределенности вида . Раскроем ее с помощью правила Лопиталя (11):

Однократное применение правила Лопиталя не приводит к раскрытию неопределенности (по-прежнему получаем ), поэтому применим его еще раз:

Таким образом, в результате двукратного применения правила Лопиталя находим, что искомый предел равен 9.

2) Убедившись, что имеет место неопределенность вида , применим правило Лопиталя:

Пример 7. Найти первую производную функции , заданной параметрически:

Решение: Дифференцируем и по параметру : , . Искомая производная от по равна отношению производных от и от по :

КОНТРОЛЬНАЯ РАБОТА №3

ИССЛЕДОВАНИЕ ФУНКЦИЙ С ПОМОЩЬЮ

ПРОИЗВОДНЫХ. ИНТЕГРАЛЬНОЕ ИСЧИСЛЕНИЕ ФУНКЦИЙ ОДНОЙ ПЕРЕМЕННОЙ

Основные теоретические сведения

1. Если в некоторой окрестности точки выполняется неравенство или , то точка называется точкой экстремума функции (соответственно точкой максимума или минимума). Необходимое условие экстремума: если - экстремальная точка функции , то первая производная либо равна нулю или бесконечности, либо не существует. Достаточное условие экстремума: является экстремальной точкой функции , если ее первая производная меняет знак при переходе через точку : с плюса на минус – при максимуме, с минуса на плюс - при минимуме.

2. Точка называется точкой перегиба кривой , если при переходе через точку меняется направление выпуклости. Необходимое условие точки перегиба: если - точка перегиба кривой , то вторая производная либо равна нулю или бесконечности, либо не существует. Достаточное условие точки перегиба: является точкой перегиба кривой , если при переходе через точку вторая производная меняет знак.

3. Прямая называется наклонной асимптотой кривой , если расстояние от точки кривой до этой прямой

стремится к нулю при .

При этом

(1)

При имеем горизонтальную асимптоту:

Если

или (2)

то прямая называется вертикальной асимптотой.

4. Общая схема исследования функции и построения ее графика.

Изучение заданной функции и построение ее графика целесообразно проводить по следующей схеме:

1⁰. Найти область определения и точки разрыва; вычислить значения функции (или соответствующих пределов) в граничных точках области определения.

2⁰. Исследовать вопрос о четности или нечетности, периодичности функции.

3⁰. Определить нули функции и интервалы ее знакопостоянства.

4⁰. Найти асимптоты.

5⁰. Определить, если это не вызовет особых затруднений, точки пересечения графика функции с координатными осями.

6⁰. Исследовать функцию на экстремум, определить интервалы ее монотонности.

7⁰. Найти точки перегиба и интервалы выпуклости и вогнутости графика функции.

8⁰. Построить график, учитывая исследование, проведенное в п.п.1⁰-7⁰.

Отметим, что эта далеко не полная схема позволяет тем не менее успешно строить графики подавляющего большинства функций, встречающихся на практике.

5. Неопределенным интегралом от функции f(x) называется выражение вида , если . Функция F(x) называется первообразной для заданной функции f(x).

При интегрировании наиболее часто используются ниже перечисленные методы.

1) Если , то

; , (3)

где a и b – некоторые постоянные.

2) Подведение под знак дифференциала:

(4)

так как

3) Формула интегрирования по частям:

(5)

Обычно выражение dv выбирается так, чтобы его интегрирование не вызывало особых затруднений. За u, как правило, принимается такая функция, дифференцирование которой приводит к ее упрощению. К классам функций, интегрируемых по частям, относятся, в частности, функции вида ,

, где P(x) – многочлен от x.

4) Интегрирование рациональных дробей, т.е. отношений двух многочленов и (соответственно k-й и n-й степени): , сводится к разложению подынтегральной функции R(x) на элементарные, всегда интегрируемые дроби вида

(6)

где l и m – целые положительные числа, а трехчлен x²+px+q не имеет действительных корней. При этом в случае неправильной дроби ( ) должна быть предварительно выделена целая часть.

5) Интегрирование методом замены переменной (способом подстановки) является одним из эффективных приемов интегрирования. Его сущность состоит в переходе от переменной x к переменной . Наиболее целесообразная для данного интеграла замена переменной, т.е. выбор функции (t), не всегда очевидна. Однако для некоторых часто встречающихся классов функций можно указать такие стандартные постановки:

где R – символ рациональной функции.

6. Формула Ньютона – Лейбница для вычисления определенного интеграла имеет вид

(7)

если и первообразная F(x) непрерывна на отрезке .

Определенный интеграл численно равен площади криволинейной трапеции, ограниченной прямыми x=a, x=b, y=0 и частью графика функции y=f(x), взятой со знаком плюс, если f(x) 0, и со знаком минус, если f(x) 0.

7. Если интервал интегрирования не ограничен (например, ) или функция f(x) не ограничена в окрестности одного из пределов интегрирования (например, при ), то по определению полагают

, (8)

(9)

Интегралы в левых частях равенств (8) и (9) называются несобственными интегралами. Несобственный интеграл называется сходящимся, если существует конечный предел в правой части равенств (8) и (9). Если же предел не существует или равен бесконечности, то несобственный интеграл называется расходящимся.

8. Пусть криволинейная трапеция, ограниченная прямыми , , и частью графика кривой , вращается вокруг оси Оx. Тогда объем полученного при этом тела вращения вычисляется по формуле

(10)

Пример 1. Исследовать на экстремум функцию

Решение: Находим первую производную: . Из уравнений и получаем точки, «подозрительные» на экстремум: , , . Исследуем их, определяя знак первой

производной слева и справа от каждой точки. Для наглядности результаты представим в виде таблицы изменения знака :

(- ,-3)	-3	(-3,-1)	-1	(-1,0)	(0,+ )
-	0	+		-	-
убыв.	min	возр.	не опр.	убыв.	убыв.

В первой строке указаны интервалы, на которые область определения функции разбивается точками , , , и сами эти точки. Во второй строке указаны знаки производной в интервалах монотонности. В третьей строке приведено заключение о поведении функции.

Исследуемая функция, как следует из таблицы, имеет минимум в точке : (-3) . Точки и не являются точками экстремума, так как в первой точке функция не определена, а в окрестности второй точки первая производная сохраняет знак.

Пример 2. Найти асимптоты графика функции .

Решение: Точка является точкой разрыва функции. Так как , то прямая служит вертикальной асимптотой графика функции [см. формулы (2)].

Ищем наклонные асимптоты , используя формулы (1):

Таким образом, уравнение наклонной асимптоты имеет вид .

Пример 3. Построить график функции , используя общую схему исследования функции.

Решение: 1⁰. Область определения – вся числовая ось, кроме точки , в которой функция терпит разрыв. Находим предельные значения функции:

2⁰. Функция общего вида, непериодическая.

3⁰. Функция имеет один нуль в точке . Функция положительна при и отрицательна при .

4⁰. График функции имеет одну вертикальную асимптоту и одну наклонную асимптоту (см. пример 2).

5⁰. График функции пересекает координатные оси в точке (0;0).

6⁰. Функция имеет один минимум при . На интервалах (- ; -3)(-1; 0)(0; + ) функция монотонно убывает, на интервале (-3; -1) – монотонно возрастает (см. пример 1).

7⁰. Вторая производная обращается в бесконечность при и равна нулю в точке , которая является единственной точкой перегиба (см. таблицу):

(- , -1)

-1

(-1, 0)

(0, + )



не опр.



точка

перегиба



На интервалах (- ; -1)(-1; 0) функция выпукла вниз (вогнута), на интервале (0; + ) – выпукла вверх. Ордината точки перегиба .

8⁰. Учитывая полученные результаты, строим график функции (рис.10).

Рис.10

Пример 4. Найти .

Решение. Так как , то, используя формулы (3), получим

Проверка:

Пример 5. Найти

Решение. Так как , то по формуле (4) находим

Пример 6. Найти

Решение. Применим метод интегрирования по частям. Положим , , тогда , . Используя формулу (5), имеем

Пример 7. Найти

Решение. Подынтегральная рациональная дробь является правильной и разлагается на элементарные дроби вида (6):

Освобождаясь от знаменателей в обеих частях этого равенства и приравнивая числители, получаем тождество для вычисления неопределенных коэффициентов А, В и С:

Составим систему трех уравнений с тремя неизвестными. Одно уравнение получим, полагая x=2 (корень знаменателя подынтегральной функции). Два других получим, приравнивая коэффициенты при одинаковых степенях х в обеих частях тождества, например при х² и х⁰:

Решение этой системы дает: А=2, В=-3, С=1. Таким образом,

Пример 8. Вычислить определенный интеграл .

Решение. Применим метод замены переменной; положим , откуда . Найдем пределы интегрирования по переменной t: при x=4 имеем t=2, а при x=9 имеем t=3. Переходя в исходном интеграле к новой переменной t и применяя формулу Ньютона – Лейбница (7), получаем

Пример 9. Вычислить несобственный интеграл или установить его расходимость: 1)

Решение. 1) Первый интеграл является несобственным интегралом с бесконечным верхним пределом интегрирования. Согласно определению (8), имеем

Следовательно, данный интеграл расходится.

2) Второй интеграл является несобственным интегралом от неограниченной функции; терпит бесконечный разрыв в нижнем пределе при x=0. Согласно определению (9), получаем

т.е. этот несобственный интеграл сходится.

Пример 10. Вычислить площадь плоской фигуры, ограниченной кривыми , , , (рис.11).

Решение.

П ример 11. Вычислить объем тела, образованного вращением вокруг оси Ох кривой

Решение. Объем полученного тела вращения найдем по формуле (10):

КОНТРОЛЬНАЯ РАБОТА №4

ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ.

КРАТНЫЕ И КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ

Основные теоретические сведения

1. Двойной интеграл можно вычислить двумя способами:

; (1)

(2)

Рис.12 Рис.13

В первом случае (рис.12) область D лежит между вертикальными прямыми и , а снизу и сверху ограничена линиями и .

Во втором случае (рис.13) надо провести горизонтальные прямые и , между которыми лежит область D, а и

- уравнения линий, ограничивающих область D слева и справа.

2. При переходе к полярным координатам (рис.14) надо декартовые координаты x, y выразить через полярные по формулам , и элемент площади заменить на .

Рис.14 Рис.15

Пусть область D лежит между двумя лучами , и изнутри угла и снаружи ограничена линями и (рис.15).

Тогда:

= (3)

3. Криволинейные интегралы 1 рода. Если кривая задана параметрическими уравнениями , ( ), то

(4)

Если кривая задана уравнением , , то

(5)

4. Криволинейные интегралы 2 рода. Если кривая задана параметрическими уравнениями , ( ), то

(6)

Если кривая задана уравнением , , то

(7)

5. Частной производной первого порядка функции двух переменных по аргументу называется предел

(8)

(приращение получает только один аргумент ). Обозначение: , . Отыскание частной производной сводится к дифференцированию функции одной переменной , полученной при фиксировании аргумента : .

Частной производной первого порядка функции двух переменных по аргументу называется предел

(9)

6. Производная в данном направлении. Градиент функции.

Если направление l в плоскости характеризуется направляющими косинусами и функция дифференцируема, то производная по направлению l вычисляется по формуле

. (10)

Градиентом функции в точке называется вектор с началом в точке , имеющий своими координатами частные производные функции :

или . (11)

Градиент указывает направление наибыстрейшего роста функции в данной точке. Производная в направлении градиента имеет наибольшее значение, равное

. (12)

7. Экстремум функции двух переменных:

Пусть функция определена в некоторой области , точка .

Точка называется точкой максимума функции , если существует такая δ-окрестность точки , что для каждой точки , отличной от , из этой окрестности выполняется неравенство .

Аналогично определяется точка минимума функции.

Необходимые условия экстремума: Если в точке дифференцируемая функция имеет экстремум, то ее частные производные в этой точке равны нулю: , .

Достаточное условие экстремума: Пусть в стационарной точке и некоторой ее окрестности функция имеет непрерывные частные производные до второго порядка включительно. Вычислим в точке значения , , . Обозначим .