конспектик / 2

70

2.1. Области применения теории графов. Основные понятия и определения. Теоретико-множественная и геометрическая интерпретация графов. Основные типы графов. Способы задания графов. Матрицы графов

Первая работа по теории графов была опубликована швейцарским математиком Леонардом Эйлером в 1736 г., когда он работал в Российской Академии наук (в Трудах Академии наук в Санкт-Петербурге). Она содержала решение популярной в то время задачи о кёнигсбергских мостах. Город Кёнигсберг (нынешний Калининград), располагавшийся тогда в Восточной Пруссии, был построен в месте слияния двух рек на их берегах и на двух островах (рис. 2.1.1). В городе было семь мостов, которые соединяли острова между собой и с береговыми частями города. Задача состояла в следующем: мог ли любой житель Кёнигсберга, выйдя из дома, пройти по всем семи мостам города в точности по одному разу и вернуться домой? Эйлер доказал невозможность такого маршрута, обобщил постановку задачи и нашёл критерий существования решения.

Рис. 2.1.1

Для доказательства того, что задача не имеет решения, Эйлер обозначил каждую часть суши точкой (вершиной), а каждый мост – линией (ребром), соединяющей соответствующие точки. Получился «граф», который показан на рис. 2.1.2, где точки отмечены теми же буквами, что и четыре части суши на рис. 2.1.1.

Рис. 2.1.2

Однако статья Эйлера более ста лет оставалась единственной работой по теории графов. Лишь в 1847 г. инженер-электрик Г.Кирхгоф применил графы для анализа электрических цепей, а в 1857 г. математик А.Кэли, занимаясь чисто практическими задачами органической химии, исследовал важный класс графов для выявления и перечисления изомеров насыщенных углеводородов. Наиболее известная нерешённая задача в теории графов – знаменитая проблема четырёх красок, впервые поставленная перед математиками де Морганом около 1850 г. Предполагается, что любую карту плоскости или поверхности шара можно раскрасить только четырьмя красками таким образом, чтобы никакие две смежные страны не были одного и того же цвета. Каждая страна должна состоять из одной связной области, а смежными называются страны, которые имеют общую границу в виде линии (а не просто одной общей точки). Каждая карта порождает граф, в котором страны (включая внешнюю область) – это вершины и две вершины соединены ребром, если соответствующие им страны смежны.

Теория графов как математическая дисциплина сформировалась только к середине тридцатых годов ХХ столетия. Термин «граф» (определение графа) впервые появился в книге выдающегося венгерского математика Д.Кёнига в 1936 г. При использовании понятия «граф» в математике чаще всего имеют в виду графическое определение (задание) связей между объектами произвольной природы. Теория графов располагает мощным аппаратом решения прикладных задач из самых различных областей науки и техники. Сюда относятся, например, анализ и синтез цепей и систем, проектирование каналов связи и исследование процессов передачи информации, построение контактных схем и исследование конечных автоматов, календарное планирование промышленного производства, сетевое планирование и управление, тактические и логические задачи, головоломки, занимательные игры, выбор оптимальных маршрутов и потоков в сетях, задачи идентификации в органической химии, моделирование жизнедеятельности и нервной системы живых организмов, исследование случайных процессов, связей между людьми и группами людей и многие другие задачи. Теория графов тесно связана с такими разделами математики, как теория множеств, теория матриц, теория групп, математическая логика, численный анализ, теория вероятностей, топология, комбинаторный анализ. За последние три-четыре десятилетия теория графов превратилась в один из наиболее бурно развивающихся разделов математики. Это вызвано запросами стремительно расширяющейся области приложений.

Граф может интерпретироваться либо как некоторая геометрическая фигура в пространстве, состоящая из точек и соединяющих их линий, либо как некоторый теоретико-множественный объект.

Пусть V – непустое множество и E – набор пар элементов множества V, причём в парах могут быть одинаковые элементы и допускается повторение пар. Тогда совокупность (V, E) называется графом G.

Будем обозначать иногда граф G G(V, E). Элементы множества V называются вершинами графа, а элементы множества E – рёбрами.

Рёбра графа могут представляться как неупорядоченными парами , так и упорядоченными . В последнем случае ребро называется ориентированным или дугой, – начальной вершиной (началом), – конечной вершиной (концом) данной дуги. Ребро или называется петлей.

Граф, состоящий из вершин и соединяющих их рёбер, называется неориентированным, а граф, состоящий из вершин и соединяющих их дуг, – ориентированным (орграфом). Графы, содержащие как рёбра, так и дуги, именуются смешанными.

Теоретико-множественное определение графа в значительной степени является абстрактным, и поэтому для введения других понятий и определений целесообразно иметь геометрическую интерпретацию графа, являющуюся более наглядной. Геометрической интерпретацией графа является рассматриваемая в евклидовом пространстве фигура Г, состоящая из точек (вершин) и соединяющих их линий, являющихся либо дугами эллипсов, либо отрезками прямых. Если все линии фигуры Г направленные, то это геометрическая интерпретация орграфа, если все линии ненаправленные – геометрическая интерпретация неориентированного графа. Геометрическая интерпретация смешанного графа содержит как направленные, так и ненаправленные линии. Петли могут быть ориентированы либо по часовой стрелке, либо против, однако ориентацию петли можно не учитывать. На рис. 2.1.3 представлена геометрическая интерпретация графа G(V, E) на плоскости, где ,,е₅={x₁,x₃},.

Рис. 2.1.3

Между графом, интерпретируемым в теоретико-множественном смысле, и его геометрической интерпретацией существует взаимно-однозначное соответствие. При этом точки соответствуют вершинам графа, а соединяющие пары точек линии – рёбрам (дугам).

П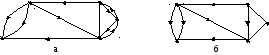ротивоположно направленные дуги орграфа, отображающие ориентацию связи в обоих направлениях, по существу равноценны неориентированной связи и могут быть заменены ребром. Произведя такую замену в орграфе, придём к смешанному или неориентированному графу. Обратно, любой неориентированный или смешанный граф можно преобразовать в ориентированный при помощи процесса удвоения, состоящего в замене каждого ребра парой противоположно ориентированных дуг с теми же начальными и конечными вершинами. На рис. 2.1.4 а и б изображены ориентированный и соответствующий ему смешанный графы.

Рис. 2.1.4

Для каждого орграфа G существует обратный граф, получаемый изменением ориентации каждой дуги G на противоположную (рис. 2.1.5). Ориентацию петли можно не учитывать.

Рис. 2.1.5

Для каждого орграфа существует также соотнесённый неориентированный граф, рёбрами которого являются рёбра первого графа, но уже без ориентаций (рис. 2.1.6).

Рис. 2.1.6

Вершины, соединённые между собой хотя бы одним ребром или дугой называются смежными. На рис. 2.1.3 смежными являются вершины и , и , и , и , и . Аналогично, два ребра, имеющие хотя бы одну общую вершину, называются смежными. На рис. 2.1.3 смежными являются рёбра и , и , и , и , и , и , и , и , и . Если ребро соединяет две вершины, т.е. или , или , то ребро называется инцидентным вершинам и или вершины и называются инцидентными ребру . Заметим, что смежность есть отношение между однородными элементами графа, тогда как инцидентность является отношением между разнородными элементами. При рассмотрении орграфов различают положительную инцидентность (дуга исходит из вершины) и отрицательную инцидентность (дуга заходит в вершину). Ориентированная петля, инцидентная вершине, считается и положительно, и отрицательно инцидентной этой вершине. В неориентированном графе рёбра, инцидентные одним и тем же вершинам, называются кратными или параллельными. В частности, две петли, инцидентные одной и той же вершине, являются параллельными. В орграфе если пара вершин инцидентна нескольким дугам, то такие две дуги называют параллельными. При этом две дуги, одинаково направленные по отношению к данной вершине, называют строго параллельными (кратными), а различно направленные – нестрого параллельными (антипараллельными).

Направленный граф – это орграф, не имеющий нестрого параллельных дуг. На рис. 2.1.7 приведены все орграфы с тремя вершинами и тремя дугами без петель и кратных дуг, два последних из них – направленные графы.

Рис. 2.1.7

Следовательно, задать граф можно, указав множества его вершин V и рёбер E и определив отношение смежности или инцидентности Ф, т.е. G(V, E, Ф). , причём для любого для орграфа и для неориентированного графа. В этом случае граф оказывается полностью определённым: символ Ф соответствует информации о том, какими рёбрами соединены между собой какие вершины графа.

Граф называется конечным, если множества его вершин и рёбер конечны (пустое множество тоже рассматривается как конечное). Ограничимся рассмотрением только конечных графов. В математике рассматриваются и бесконечные графы, но в практических приложениях они встречаются редко.

Назовём граф обыкновенным или простым, если в нём отсутствуют петли и кратные рёбра (дуги). Граф, имеющий кратные рёбра (дуги), называется мультиграфом, а граф, в котором есть хотя бы одна петля, называется псевдографом. Так, граф на рис. 2.1.2 является только мультиграфом, а графы на рис. 2.1.3 и 2.1.8 – мультиграфы и псевдографы.

Рис. 2.1.8

Два графа G и H изоморфны (записывается ), если между их множествами вершин существует взаимно-однозначное соответствие, сохраняющее смежность. Если рёбра ориентированы, то их направления также должны соответствовать друг другу. Например, графы на рис. 2.1.9 изоморфны, а графы на рис. 2.1.10 не изоморфны.

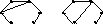
Рис. 2.1.9 Рис. 2.1.10

Очевидно, что отношение изоморфизма графов является эквивалентностью, т.е. оно рефлексивно, симметрично и транзитивно. Следовательно, множество всех графов разбивается на классы так, что графы из одного класса попарно изоморфны, а графы из разных классов не изоморфны. Изоморфные графы естественно отождествлять, т.е. считать совпадающими (их можно изображать одним рисунком).

В некоторых ситуациях всё же приходится различать изоморфные графы, в связи с чем вводится понятие «помеченного графа». Граф называется помеченным (или перенумерованным), если его вершины отличаются одна от другой какими-либо пометками, например, . Графы на рис. 2.1.2 и 2.1.3 помеченные, на рис. 2.1.4–2.1.10 – непомеченные.

Инвариант графа G – это число, связанное с G, которое принимает одно и то же значение на любом графе, изоморфном G. Так, число вершин и число рёбер являются инвариантами графа.

Подграфом (или частью) графа G называется граф , у которого все вершины и рёбра принадлежат G. Пусть задан граф G(V, E, Ф), где Ф – отношение инцидентности. Систему будем называть подграфом графа G тогда и только тогда, когда выполняются следующие условия:

1.

2. для каждого .

3. Если и или , то

Если – подграф графа G, то G называется надграфом графа . Остовный подграф – это подграф графа G, содержащий все его вершины. Для любого подмножества вершин графа G порождённым подграфом <> называется подграф , множеством вершин которого является , а множеством рёбер – множество всех рёбер G, оба конца которых принадлежат . Таким образом, вершины из смежны в <> тогда и только тогда, когда они смежны в G. Рассматриваются также подграфы, порождённые множествами рёбер. Для подмножества множества рёбер графа G множество рёбер порождённого подграфа <> совпадает с , а множество вершин – со множеством всех концов рёбер из .

Рис. 2.1.11

На рис. 2.1.11 – подграф графа G, порождённый множеством вершин и множеством рёбер, не являющийся остовным. – остовный подграф G, порождённый множеством рёбер, но не множеством вершин. – не порождённый множеством вершин, не порождённый множеством рёбер, не остовный подграф графа G.

Обыкновенный неориентированный граф называется полным, если любые две различные его вершины смежны. Обыкновенный орграф называется полным, если в нём любые две различные вершины соединены парой антипараллельных дуг. Существует единственный с точностью до изоморфизма полный неориентированный или ориентированный граф с фиксированным числом вершин p и обозначается символом . Если в каждую вершину полного графа добавить по одной петле, то получившийся граф будет называться насыщенным. Граф называется нуль-графом, если он не имеет рёбер (E=). Нуль-граф с фиксированным числом вершин р единственный с точностью до изоморфизма и обозначается . На рис. 2.1.12 показаны соответственно полные ориентированный и неориентированный графы и , а также насыщенные неориентированный и ориентированный графы с пятью и тремя вершинами и нуль-граф .

Рис. 2.1.12

Двудольный граф (или биграф) – это граф, множество вершин V которого можно разбить на два непересекающихся подмножества (доли) V₁ и V₂ таким образом, что не существует рёбер, инцидентных вершинам одного и того же подмножества. В общем случае граф называется k-дольным, если множество его вершин можно разбить на k непересекающихся подмножеств V₁,…,V_k так, что не существует рёбер, инцидентных вершинам одного и того же подмножества. Обыкновенный неориентированный граф называется полным k-дольным, если любые две вершины, входящие в различные доли, смежны. Обыкновенный ориентированный граф будет полным k-дольным, если любые две вершины из различных долей соединены парой антипараллельных дуг.

Полный k-дольный граф, доли которого состоят из p₁,…p_k вершин, единственный с точностью до изоморфизма и обозначается символом Звездой называется полный двудольный граф K_1,p. Заметим, что одна из долей двудольного графа может быть пустой. Так, O₁ – двудольный граф с одной пустой долей, O₂ можно трактовать как двудольный граф с двумя одновершинными долями или как двудольный граф, одна из долей которого содержит две вершины, а другая является пустым множеством. Чтобы подчеркнуть отмеченную особенность k-дольного графа, его часто изображают, размещая подмножества вершин V₁,…,V_k в разных столбцах или строках. На рис. 2.1.13 изображены трёхдольный ориентированный граф, полный двудольный неориентированный граф K_3,3, ориентированная звезда K_1,4 соответственно.

Рис. 1.13

Число рёбер неориентированного графа, инцидентных вершин v, называется степенью или порядком этой вершины. При подсчёте числа рёбер, инцидентных вершине v, некоторую неопределённость вносит петля, так как её можно считать и как единственное, и как двойное ребро. В зависимости от рассматриваемой задачи может оказаться более удобным как тот, так и другой способ подсчёта. Таким образом, в каждом случае должно быть указано, считается петля однократной или двойной. Будем обозначать степень вершины v через d(v) (или deg(v)). Максимальная и минимальная степени вершин графа G обозначаются символами (G) и (G) соответственно:

, .

Изолированными называются вершины, которые не являются концами рёбер и не связаны ни между собой, ни с другими вершинами. Изолированность вершины v в неориентированном графе эквивалентна условию d(v)=0. Вершина степени 1 (единица) называется концевой или висячей вершиной, если петля считается двойной.

Если считать, что каждая петля вносит в степень соответствующей вершины двойку, то мы приходим к утверждению, которое установлено Эйлером и является исторически первой теоремой теории графов.

Теорема 2.1.1. Сумма степеней вершин неориентированного графа равна удвоенному числу его рёбер:

.

Поскольку каждое ребро, не являющееся петлёй, инцидентно двум вершинам, в сумму степеней вершин графа оно вносит двойку. Каждая петля также вносит двойку в сумму степеней вершин графа.

Следствие. В неориентированном графе число вершин с нечётными степенями чётно.

Разобьём множество вершин V графа G на два подмножества. и – соответственно множества вершин графа, имеющих чётные и нечётные степени. Так как и , то по теореме 2.1.1.

Тогда – чётное число. Так как все d(v) нечётны для , то должно быть чётным числом.

Неориентированный граф, степени всех вершин которого одинаковы и равны r, называется r-однородным (регулярным), однородным графом степени r. Примером однородных неориентированных графов являются графы, составленные рёбрами и вершинами пяти правильных многогранников или платоновых тел: тетраэдра (), куба (), октаэдра (), додекаэдра (), икосаэдра () (рис. 2.1.14).

Степень регулярного графа G обозначается deg G. На рис. 2.1.15 приведены примеры 3-однородных (или кубических) неориентированных графов (петля учитывается дважды). На рис. 2.1.16 приведены примеры двух бесконечных 4-однородного и 8-однородного графов.

Рис. 2.1.14

Рис. 2.1.15

Рис. 2.1.16

Рассмотрим теперь случай ориентированного графа. Если обозначить символом множество дуг, входящих в вершину v, а символом множество дуг, выходящих из вершины v, то тогда число называется полустепенью входа (захода) этой вершины, а число – полустепенью выхода (исхода) вершины v.

При вершина v называется изолированной, при – выходом, при – входом.