конспектик / 2

105

2.3. Реализуемость графов в трёхмерном пространстве. Графы плоские и планарные. Теорема Понтрягина-Куратовского

В связи с использованием геометрической интерпретации графа рассмотрим класс графов, известных под названием геометрических графов.

Обозначим n-мерное евклидово пространство через . Евклидово n-мерное пространство есть множество всех последовательностей из n вещественных чисел (точек), в котором расстояние между любыми двумя точками и определено следующим образом: .

Простой незамкнутой кривой в пространстве называется непрерывная самонепересекающаяся кривая, соединяющая две различные точки в (т.е. кривая, получаемая непрерывной деформацией прямолинейного отрезка). Аналогично, простой замкнутой кривой называется непрерывная самонепересекающаяся кривая, конечные точки которой совпадают. Геометрический граф в пространстве есть совокупность множества точек пространства и множества простых кривых, удовлетворяющих следующим условиям:

1. каждая замкнутая кривая в E содержит только одну точку v множества V;

2. каждая незамкнутая кривая в E содержит ровно две точки множества V, которые являются её граничными точками;

3. кривые в E не имеют общих точек, за исключением точек множества V.

Ориентированный геометрический граф в пространстве есть совокупность множества точек V и множества простых направленных (или ориентированных) кривых, удовлетворяющих тем же условиям 1–3. Ориентацию можно интерпретировать как направление передвижения по ребру. Смешанный геометрический граф содержит как направленные, так и ненаправленные кривые.

С позиций теории графов точки множества V геометрического графа называются геометрическими вершинами, а простые кривые множества E – геометрическими рёбрами (дугами). На геометрические графы распространяются, таким образом, все понятия и определения теории графов.

Если граф изоморфен геометрическому графу ^/, то ^/ называется геометрической реализацией графа . В частности, геометрический граф можно рассматривать как геометрическую реализацию самого себя. Будем говорить, что граф реализуем в пространстве , если существует его геометрическая реализация в .

Любой ли граф можно реализовать в евклидовом пространстве для некоторого соответствующего натурального числа n? Если этот вопрос решается положительно, то интересно знать, существует ли такое число , что всякий граф допускает реализацию в пространстве Е ^? В последнем случае желательно знать минимальное значение . Ответ на этот вопрос даёт теорема о реализуемости графов в трёхмерном пространстве.

Теорема 2.3.1. Любой конечный граф G(V,E) имеет геометрическую реализацию в трёхмерном евклидовом пространстве .

Путь и . Выберем в произвольную прямую L и на ней разместим p различных точек , поставив их во взаимно-однозначное соответствие вершинам графа . Затем через выбранную прямую L проведём пучок из q различных полуплоскостей, поставив их во взаимно-однозначное соответствие рёбрам графа . В каждой полуплоскости, соответствующей ребру (), соединим точки и простой кривой (направленной кривой). Выполнив такое построение для всех рёбер графа в соответствующих полуплоскостях, получим в фигуру Г, являющуюся геометрической реализацией графа G(V,E), т.к. все простые кривые, соответствующие рёбрам данного графа, лежат в различных полуплоскостях и не имеют общих точек кроме точек прямой L, соответствующих вершинам графа.

Приведённая теорема не допускает понижения размерности евклидова пространства, в котором мог бы быть реализован любой степени сложности конечный граф. Однако существует класс графов, реализуемых в пространстве , т.е. на плоскости. Граф, реализуемый в пространстве , называется планарным. Геометрический граф в пространстве называется плоским. Плоский и соответствующий ему планарный графы изоморфны. Примеры плоских графов даны на рис. 2.3.1.

Рис. 2.3.1

Граф G, изображённый на рис. 2.3.2, планарен, т.к. он изоморфен плоскому графу G^/

Аналогично определению геометрического графа в пространстве можно дать определение геометрического графа на поверхности S. Говорят, что граф укладывается на поверхности S, если существует изоморфный ему геометрический граф на поверхности S.

Теорема 2.3.2. Граф укладывается на сфере тогда и только тогда, когда он планарен.

Для доказательства этой теоремы достаточно рассмотреть стереографическую проекцию (рис. 2.3.3). Путь граф G – геометрический граф на сфере. Проведём плоскость Q, касательную к сфере, так, чтобы северный полюс N (точка, диаметрально противоположная точке касания) не лежал на ребре и не совпадал с вершиной графа G. Теперь рассмотрим граф G^/, полученный стереографической проекцией графа G из точки N на плоскость Q. Поскольку существует биективное соответствие между точками сферы, отличными от N, и их стереографическими проекциями, то граф G^/ плоский и изоморфен графу G. Следовательно, G – планарный граф. Значит, и граф, изоморфный G, который укладывается на сфере, также планарный.

Обратное утверждение доказывается аналогично с учётом установленной биекции.

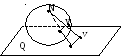
Рис. 2.3.3

Планарность является существенным свойством графов, которые моделируют коммуникации и связи между объектами на плоскости (дороги между населёнными пунктами, водопроводные и газопроводные сети, линии передач электроэнергии, межсоединения на печатных платах электронных устройств и кристаллах интегральных схем). Плоскими графами представляются различные карты, с которыми, в частности, связана известная проблема четырёх красок (§ 2.1). В 1890 г. П. Хивуд доказал, что для требуемой раскраски карты достаточно пяти красок, но никто ещё не привёл примера, когда пять красок действительно необходимы. Контрпример, если его найдут, обязательно будет чрезвычайно большим и сложным, поскольку О. Оре и Г. Стемпл доказали в 1969 г. справедливость гипотезы для всех карт, содержащих меньше 40 стран. Граф, соответствующий карте на плоскости или сфере, можно нарисовать на плоскости без пересечения рёбер (в точках, отличных от вершин графа). Таким образом, если удалось бы показать, что вершины любого планарного графа можно раскрасить четырьмя или меньшим числом красок так, чтобы смежные вершины имели разные цвета, то гипотеза четырёх красок была бы обоснована.

Свойство планарности не нарушается при операции подразделения ребра графа и обратной подразделению ребра операции. Если граф планарный, то очевидно, что любой граф, гомеоморфный ему, также является планарным.

Исторически первым критерием планарности графов является следующий критерий, доказанный Л.С. Понтрягиным в 1927 г. и К. Куратовским в 1930 г. независимо друг от друга.

Теорема 2.3.3 (Понтрягина-Куратовского). Граф планарен тогда и только тогда, когда он не содержит подграфов, гомеоморфных и .

Строгое доказательство теоремы Потрягина-Куратовского приведено в [2, 3, 4, 6].

Граф (рис. 2.3.4) – это полный граф с пятью вершинами. Он является предельным графом в том смысле, что если рассматривать последовательность полных графов K_p, то граф K₅ будет непланарным графом с минимальным числом вершин. Графы – планарные (рис. 2.3.4).

Рис. 2.3.4

Двудольный граф (рис. 2.3.5) является моделью задачи о трёх городах и трёх источниках снабжения. Имеются три города a, b, c и три источника снабжения: водонапорная башня d, газовый завод e, электростанция f (см. рис. 2.3.5); каждый из городов связан с каждым источником снабжения соответственно водопроводом, газопроводом, линией электропередачи. Можно ли начертить (на плане) три города, три источника и все линии передачи таким образом, чтобы никакие две линии не пересекались между собой в неконцевых точках? Непосредственные попытки показывают, что всегда можно нарисовать восемь линий, а девятая обязательно пересечёт хотя бы одну из этих восьми.

Данная ситуация является следствием того, что граф не является планарным. Эта задача хорошо известна также как задача о трёх домах и трёх колодцах. Можно ли так проложить дорожки от всех домов к каждому колодцу, чтобы они не пересекались? Это соответствует ситуации, когда поссорившиеся соседи не желают встречаться, но хотят пользоваться всеми колодцами.

Рис. 2.3.5

Ориентированный граф является планарным тогда и только тогда, когда соотнесённый ему неориентированный граф является планарным.