
Шпоры по отуис, 1ый семестр (Иванов НН) [6584 вопросов] / Otvety_k_ekz_OTUiS_Dnevnoe_12-13_1
.pdf
2.При умножении случайного процесса X(t) на постоянное значение с значения функции автоковариации увеличи-ваются в с2 раз.
3.При умножении случайного процесса X(t) на неслучайную функцию f(t) автоковариация увеличивается в f(t1) f(t2) раз.
4.Функция автоковариации стационарного процесса зависит только от разности времени τ=
t2 - t1: RXX(t1, t2) = RXX(t, t+τ) = RXX(τ).
Это следует из того, что в стационарном процессе для любого момента времени t совместные распределения от аргументов t, t+τ совпадают. Ввиду этого свойства функция автоковариации
стационарного процесса записывается в виде RXX(τ). 5. Для стационарного процесса RXX(0) ≥ RXX(τ).
Это следует из того, что математическое ожидание неотрицательной величины
Добавим в скобки +m и –m , обозначим  , тогда ввиду неотрицательности мат ожидания неотрица-тельной величины
, тогда ввиду неотрицательности мат ожидания неотрица-тельной величины
Отсюда
Но процесс X(t) стационарный, поэтому 
(дисперсия стационарного процесса не зависит от момента времени t).
Тогда
Это свойство подтверждает ясный по смыслу факт, что наибольшая взаимосвязь в стационарном сигнале наблюдается при t1 = t2, (τ=0) это очевидно, так как со временем зависимость сигнала от того, что было в прошлом ослабевает.
77.Спектральная функция мощности. Энергия телеграфного сигнала.
Фурье-образ автокорреляционной функции позволяет оценить энергию случайного
сигнала в частотном диапа-зоне. Для автоковариационной функции RXX(τ) положим
R XX( ) F( RXX( )) |
RXX( )e i d |
|
|
Для автокорреляционной функции KXX(τ) преобразование Фурье имеет вид |
|
|
|
K XX( ) F( K XX( )) |
K XX( )e i d |
Функция называется спектральной функцией плотности мощности процесса или просто спектральной функцией мощности процесса (или спектральной функцией
процесса).
Если процесс стационарный, то обе функции четные, тогда вместо преобразования Фурье можно применить косинус-преобразование.
Поясним, при чем тут мощность. Обратное преобразова-ния Фурье для 
|
|
1 |
|
|
|
|
|
|
|
|
|
|
K XX |
|
|
K XX ei d |
|
|
|
|
|
|
|
||
|
2 |
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
t |
|
|
|||
При τ = 0 |
K |
XX |
M X t X t 0 |
M X 2 |
|
|
|
x2 p( x , x; 0 )dxdx |
||||
|
|
|
|
|
|
|
|
|
||||
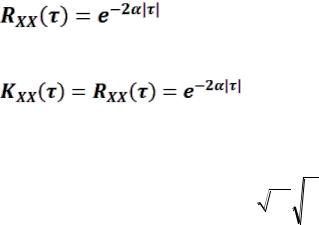
То есть, получено выражение для энергии сигнала на всей оси времени, энергия равна интегралу в частотной области от функции спектральной мощности:
|
|
1 |
|
|
K XX 0 |
|
K XX d |
||
2 |
||||
|
|
|
||
|
|
|
Так как функции автокорреляции и спектральной плотности связаны преобразованием Фурье, то для них справедливо равенство Парсеваля
|
K XX |
|
2 d |
1 |
|
K XX |
|
2 d |
|
|
|
|
|||||
|
2 |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Мы вывели выражение для оценки энергии сигнала в частотной области, это интеграл (с коэффициентом, который опущен)

Оценить энергию случайного сигнала, рассеиваемую в диапазоне [ω1, ω2] можно
определенным интегралом

Энергия телеграфного сигнала
Пример. Найти 50-процентный энергетический диапазон частот [- ω0, ω0] телеграфного сигнала.
Телеграфный сигнал – стационарный процесс с автоковариационной функцией  для неотрицательных τ, функция четная, продолжая ее по четности для отрицательной полуоси, получаем
для неотрицательных τ, функция четная, продолжая ее по четности для отрицательной полуоси, получаем
o
Математическое ожидание телеграфного сигнала m = 0, поэтому автокорреляционная функция  совпадает с автоковариационной функцией,
совпадает с автоковариационной функцией,
|
o |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Преобразование Фурье функции |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
K XX |
F K XX |
|
|
e i d |
|
|
|
|
|||||||||||
|
K XX |
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
2 |
|
|
e 2 cos( )d = |
2 |
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
4 |
2 |
2 |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
K XX d |
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
d 2 6.28 |
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
||||||||||||
4 |
2 |
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Для решения задачи следует найти ω0 такое, что
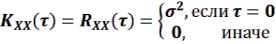
0 |
|
|
d |
0 |
|
|
4 |
|
|
|
|
|
|
|
|
||||
K XX |
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
d |
4Arctg |
0 |
|
3.14 |
|||||||||
|
|
|
|
2 |
|
|
|||||||||||||
|
|
|
|
|
|
|
4 |
|
|
|
|
2 |
|
|
|||||
0 |
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
3.14 |
|
|
|
|
|
|
|
|
|
|
|
|
|
Arctg |
|
|
0 |
|
|
|
|
0.785 |
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
2 |
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
tg( 0.785) 1 |
|
|
|
|
|
|
|
|
|
||||||
2 |
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
0 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
При α =1 частота ω0 = 2, то есть при частоте 0 ¸ 0.318Hz телеграфный сигнал рассеивает (потребляет) 50% своей энергии.
78. Определение белого шума. Гауссовский белый шум.
Стационарный в узком смысле случайный процесс с функцией спектральной плотности мощности, равной положи-тельной постоянной величине, называется белым шумом.
Обычно в процессе белого шума математическое ожидание равно нулю, m = 0.
Так как белый шум стационарный в узком смысле процесс то его автокорреляционная функция зависит от одного аргумента τ;
KXX(τ) является четной.
Функция спектральной плотности KXX(ω) получается из автокорреляционной функции косинус-преобразованием. Пусть KXX(ω) = c > 0. Обратное преобразование Фурье (обратное косинус-преобразование) постоянной функции равно δ-функции с коэффициентом
|
|
|
1 |
|
|
K XX( ) F 1(K XX( )) |
K XX( )ei d |
||||
2 |
|||||
|
|
|
|
||
|
|
|
|
||
|
1 |
|
|
|
|
|
cei d c ( t) |
|
|
||
2 |
|
|
|||
|
|
|
|
||
|
|
|
|
||
Следовательно, белый шум – некоррелированный процесс, случайные величины X(t1) и X(t2) для любых  некоррелированы (независимы). Распределение случай-ной величины X(t0) в определении белого шума не уточ-няется, оно может быть любым.
некоррелированы (независимы). Распределение случай-ной величины X(t0) в определении белого шума не уточ-няется, оно может быть любым.
Энергия сигнала пропорциональна интегралу
|
|
1 |
|
|
|
|
1 |
|
|
M E |
|
|
K |
XX |
( )d |
|
|
cd |
|
|
|
||||||||
|
|
2 |
|
|
2 |
|
|||
|
|
|
|
|
|
|
|
||
Отсюда следует, что белого шума не существует.
Рассмотрим стационарный некоррелированный гауссовский процесс.
Пусть математическое ожидание процесса a = 0, средне-квадратическое равно σ. Тогда ввиду нулевого математи-ческого ожидания
Если σ стремится к бесконечности, то такой гауссовский процесс стремится к белому шуму. Но в реальном при-ложении приходится ограничиться конкретным значени-ем среднеквадратического σ . Положим σ = 10 , и найдем спектральную плотность такого процесса.
Найти преобразование Фурье функции KXX(τ) гауссовского процесса можно предельным переходом (при ε стремится к 0) преобразования Фурье прямоугольного импульса R(σ2, ε, t)
|
|
|
|
2a |
|
|
|
|
z |
||
F (R(a, , t)) |
|
|
sin z |
|
|
a sinc |
|
|
|||
|
|
|
|
||||||||
|
|
|
|
z |
|
2 |
|
|
|
2 |
|
|
2 |
|
|
|
2 |
z |
|
|
|||
F (R( |
|
, , t)) |
sinc |
|
|
|
|
|
|||
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
2 |
|
|
||
В правой части получена функция, которая при ε * 0 стремится к спектральной функции плотности KXX(ω) белого шума.
Таким образом, стационарный некоррелированный гаус-совский процесс можно рассматривать как приближение к белому шуму. Это реально используется в практических задачах.
79. Физические источники белого шума.
В природе существуют случайные физические явления, близкие к белому шуму. В достаточно широком диапазоне спектральная плотность мощности таких процессов приближенно равна постоянной величине.
Рассмотрим такие природные явления, возникающие в радиотехнике. Тепловой шум электрической цепи.
o Этот шум появляется в сопротивлениях цепи усиления сигнала. Вместе с сигналом усилитель увеличивает амплитуду шума. Это шум сопротивлений усилителя, а не атмосферных явлений.
Источник шума – тепловое хаотическое движение электронов в сопротивлениях (в проводниках).
Ток (или напряжение), текущий между катодом и анодом электронной лампы.
Низкочастотный шум, другое название : 1/f - шум (flicker noise) возникает во многих радиоэлектронных устройствах, его источник – отклонения в кристалличес-кой структуре полупроводников и неоднородность моле-кул углерода в сопротивлениях, этот шум увеличивается при уменьшении частоты сигнала.
Дробовой шум – пульсация на высоких частотах (burst noise, popcorn noise), возникает из-за посторонних вкрап-лений в полупроводниковые материалы и появления ионов легких элементов в электрических схемах; ампли-туда этого шума достаточно высокая; он проявляется, например, при источнике звука до 100Гц из микрофона,
при этом ясно слышны разрыва кукурузных зерен на сковороде; этот шум фильтруется очень плохо.
Лавинообразный шум – его источник находится на p-n переходе полупроводников, когда на разделяющую поверхность воздействует электромагнитное поле с направленностью, противоположной протеканию электронов в данном полупроводнике; поле направляет «дырки» в противоположном направлении; после достижения определенного порога электроны лавиной заполняют «дырки» и генерируют сигнал с резким скачком, похожим на
δ-функцию.
80.Коррелированность случайных процессов.
Рассмотрим два случайных процесса X1(t) и X2(t) , для простоты изложения мы ограничимся только стационар-ными процессами, хотя все результаты легко обобщить на нестационарный случай.
Пусть для каждого из них известны параметры, такие, как математическое ожидание
o m1 = M[X1(t) ], |
m2 = M[X2(t) ]; |
Дисперсия: D1 = σ1 2 = M[(X1(t) – m1)2], o D2 = σ2 2 = M[(X2(t) – m2)2];
Автоковариация:
Автокорреляция
Взаимозависимость случайных процессов X1(t) и X2(t) можно полностью описать взаимными многомерными функциями распределения (или плотностями распределений).
На практике ограничиваются взаимными функциями ковариации (и корреляции).
Для двух случайных процессов X(t) и Y(t) взаимной функцией ковариации называется
взаимной функцией корреляции
Взаимной спектральной плотностью называется Фурье-образ функции взаимной корреляции
KXY(ω) = F(KXY(t)).
81.Мат ожидание и дисперсия для стохастической свертки.
Если сигнал задан уравнением
Возьмем математическое ожидание от обеих частей равенства. Ядро свертки – детерминированная функция, случайными являются только входной и выходной сигналы. Тогда в правой части можно внести функцию математического ожидания под интеграл. Если интеграл с новым подынтегральным выражением существует, то такое внесение под интеграл допустимо.
Если рассматривать только стационарные процессы, то получим равенство
Таким образом, интеграл от ядра дает коэффициент усиления средних значений входа, можно сказать, что этот интеграл дает средний коэффициент усиления во всей временнОй области.
Для реальных задач пределы интегрирования ограничиваются конечным интервалом [0, M], тогда средний коэффициент усиления системы во временнОй области равен
o
Дисперсию можно вычислять как
o
Найдем M[(Y(t))2] :
записывая правую часть как произведение интегралов, а лучше как двойной интеграл с разными (во избежание путаницы при интегрировании) переменными интегрирования, получаем:
 Применяя автоковариацию, получаем
Применяя автоковариацию, получаем
|
Y ( t) 2 |
|
|
|
M |
|
RXX( 2 1)h( 1)h( 2 )d 2 d 1 |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
82.Идентификация модели стохастической свертки.
Пусть 
Умножим обе части уравнения свертки на случайный сигнал X(t- ν). Так как аргумент сигнала на зависит от переменной интегрирования, то в правой части этот сигнал можно внести под интеграл.
Возьмем математическое ожидание от обеих части уравнения, считая, что сигналы зависят от времени t, а аргументы τ и ν - параметры. Математическое ожидание – это интеграл, в правой части математическое ожидание можно внести под знак интеграла.
Так как сигналы стационарные, то математическое ожидание в левой части
Аналогично в правой части
Возьмем преобразование Фурье от обеих частей
K XY H K XX
Если сигналы X(t), Y(t) известны, то можно найти и их автокорреляции и их взаимную корреляцию. Осталось выразить неизвестное H(ω) через эти корреляционные функции.
H = KK
XY
XX

Вычислив обратное преобразование Фурье, получим искомую функцию ядра свертки, что заканчивает решение задачи идентификации.
h t =F-1 |
|
K |
|
||
|
|
K |
|
|
XY
XX
Возвращаясь к равенству
заметим, что если X(t) – белый шум с нулевым математи-ческим ожиданием, то его функция автокорреляции (она равна функции автоковариации) является δ-функцией, умноженной на некоторую положительную постоянную
Тогда свертка импульса с ядром дает
h( ) C ( )d C h( ),
h( ) 1 K ( )
С некоторой натяжкойXY можно сказать, что белый шум для случайных сигналов аналогичен
C
импульсу для детерминированных сигналов.
83.Идентификация модели стохастической свертки с шумом.
В реальных задачах приходится учитывать влияние шума на выходной (и входной) сигнал. Пусть Z(t) – процесс с нулевым математическим ожиданием, который наклады-вается на выход системы (аддитивный шум) . Если систе-ма моделируется в виде суммы свертки и аддитивного шума, который не зависит от входного сигнала X(t), то модель системы:
как и в предыдущем примере, умножим на X(t- ν). Вычислим математическое ожидание от обеих частей, учитывая независимость процесса шума от других процес-сов. Для шума получаем
Это означает, что в соотношении корреляционных функ-ций шум исчезает и окончательно формулы для ядра свертки совпадает с формулой предыдущей модели без учета шума
h t =F-1 |
|
K |
|
||
|
|
K |
|
|
XY
XX
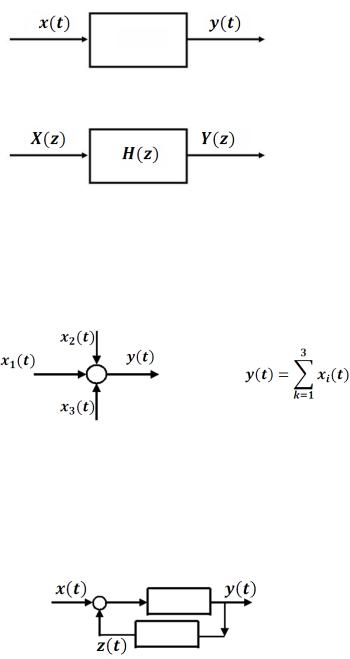
84. Модель системы. Передаточная функция. Моделирование обратной связи.
Предположение о линейности (в различных смыслах) явления, процесса, зависимости – это упрощение, которое облегчает решение задачи. Если при этом получается удовлетворительный результат, то исследование завершается.
Но в большинстве случаев результат, полученный в предположении линейности далек от желаемого и приходится усложнять модель. Для динамической системы простейшей функциональной моделью является модель свертки. На схеме она обозначается как
Это свертка во временной области.
В частотной области свертка соответствует умножению Фурье-образов входного сигнала X(z) на функцию H(z) :
Функция H(z) называется передаточной, это Фурье- (или Лаплас-) образ ядра свертки.
Изображение системы в виде схемы во многих случаях удобнее, чем другие модели. Схема не описывает все детали математической модели, но дает представление о компонентах системы.
Сигналы, изображенные на схеме могут быть как детерминированными, так и случайными, мы будем отличать их по используемым шрифтам.
Сумматор на схеме изображается окружностью, сумма входящих сигналов равна единственному выходящему.
Кроме обычных последовательных блоков система может содержать обратные связи, это ситуации, когда выходной сигнал корректирует входной сигнал.
Простейший естественный пример обратной связи – костер и ведро с кипящей водой.
Здесь входной параметр – количество теплоты, получаемое водой от костра, выходной параметр – уровень воды в ведре. Когда огонь разгорается сильно, уровень кипящей воды повышается и заливает огонь. Это уменьшает входной параметр (огонь), вызывая уменьшение выходного параметра.
Схема обратной связи
o
