Шпоры по отуис, 1ый семестр (Иванов НН) [6584 вопросов] / Otvety_k_ekz_OTUiS_Dnevnoe_12-13_1

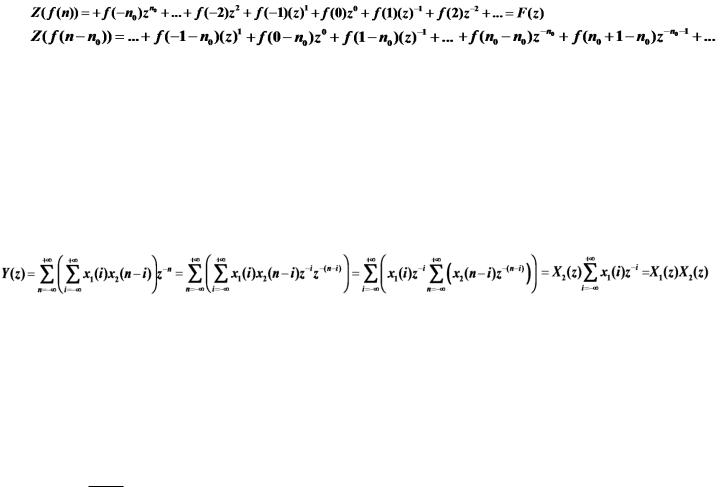
65.Свойства z-преобразования и их доказательства.

Линейность

Z(a f(n) + b g(n)) = a F(z) + b G(z)

Свойство сдвига (задержки)

Z(f(n-n0)) = F(z) z -n0

Доказательство: z-преобразование сигнала со сдвигом f(n - n0), если Z(f(n))=F(z). Сравним два ряда

Предполагая, что ряды сходятся абсолютно, первый ряд, равный F(z), умножим на z-n0 и получим второй ряд. То есть

Z( f (n n0 )) F(z)z n0

z-преобразование свертки

Если y(n) – свертка сигналов x1(n) и x2(n) , то

Y(z) = X1(z) X2(z)

Доказательство: утверждение доказывается перестановкой членов ряда.

66.Обратное z-преобразование. Диапазон частот и изменение периода дискретизации сигнала.

f (n) 21i СF (z )z n 1dz

C

 Интегральное преобразование определенное для всех целых чисел n называется обрат-ным z-

преобразованием. С – замкнутый контур, включа-ющий все полюсы функции F(z) или прямая z = C, где С – вещественное число, по модулю бОльшее модулей всех полюсов функции F(z) .

 При инженерном использовании z- преобразования обратное преобразование находят по таблицам, не применяя интегрирование.

 Для рациональных функций обратное z-преобразование вычисляют разложением рационального выражения на сумму элементарных дробей. При этом вместо дробей вида

67.Коэффициент усиления фильтра.

Основное назначение фильтра – усиление входного сигнала в зависимости от диапазона частоты. Для решения этой задачи фильтр исследуется в частотной области. Если речь идет о цифровых сигналах, то разумно применять z-преобразование.

Для оценки воздействия фильтра на входной сигнал используется понятие усиления сигнала. Усилением (коэффициентом усиления) сигнала на частоте w называется отношение:

g(w ) Amp(y (w )) ,

Amp(x (w ))

где Amp(x(w)) , Amp(y(w)) – максимальные модули амплитуд входного и выходного синусоидальных сигналов на частоте w.

В отличие от других задач теории сигналов, при анализе и проектировании фильтров рассматривают 1) только синусоидальные сигналы; 2) для этих сигналов принимают во внимание только амплитуды. В других задачах самыми важными характеристиками могут быть фазы сигналов.

68.Случайные величины и их характеристики.

Основные числовые характеристики непрерывной случайной величины X(ω) - это математическое ожидание

дисперсия

и среднеквадратическое отклонение

Для экономии времени будем обозначать эти характеристики mX, DX, σX, или просто m, D,

σ.

Важнейшим в приложениях является нормальное распределение, которое полностью описывается двумя своими параметрами :

a – математическое ожидания и σ - среднеквадратическое отклонение.

Его функция распределения N(a, σ)

Функция плотности нормального распределения:

Во многих ситуациях бывает необходимо оценить взаимное влияние двух случайных величин. Для этого вводится ковариация случайных величин X и Y,

где mX, mY – математические ожидания.

Если случайные величины X и Y независимы, то их ковариация равна нулю (обратное не всегда верно).

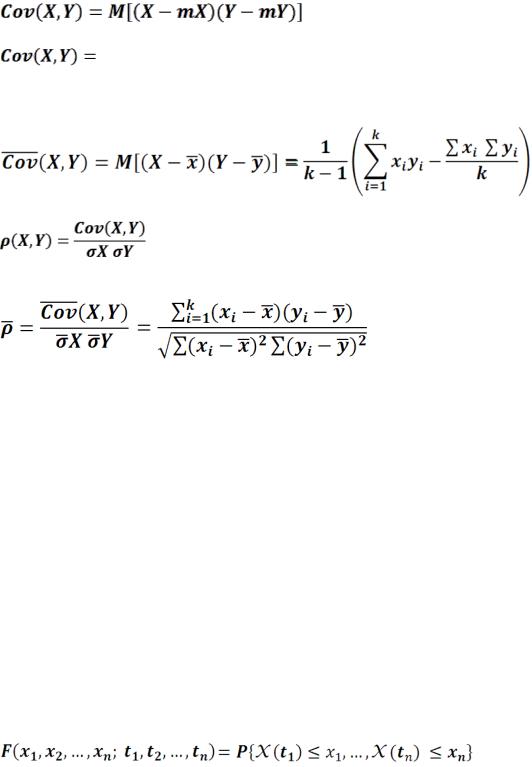
Ковариация случайной величины X с собой равна дисперсии этой величины :

Для любых двух случайных величин X и Y можно построить их совместную функцию распределения F( x,y) и, возможно, их совместную функцию плотности p( x, y).

Если p( x, y) – совместная функция плотности случайных величин X и Y, то

x mX y mY p( x, y)dxdy

В статистике при k наблюдениях пары случайных величин оценка ковариации вычисляется как

Коэффициентом корреляцией случайных величин X и Y называется

В статистике при k наблюдениях оценка коэффициента корреляции случайных величин X и Y вычисляется по формуле

69.Случайный процесс и его характеристики.

Случайным процессом называется такая случайная функция времени X(t) , определенная на

некотором конечном или бесконечном интервале времени, что для любого t0 функция X(t0) является случайной величиной. Для любого фиксированного t0 случайная величина X(t0) имеет функцию распределения F(x, t0) и может иметь функцию плотности распределения p(x, t0).

Функции распределения F(x, t0) и функции плотности распределения p(x, t0) в общем случае различные для различных t0, но могут и совпадать. Функция плотности p(x, t0) полностью определяет случайную величину X(t0) в момент t0.

Но и функция распределения, и функция плотности не содержит информации о взаимосвязи

со случайной величиной X(t1) в другой момент времени t1. Эта взаимосвязь описывается двумерной функцией плотности распределения p(x1, x2; t1,t2). Взаимосвязь трех случайных величин случайного процесса X(t) описывается трехмерной функцией плотности

распределения p(x1, x2, x3; t1,t2,t3), и так далее. Для полного описания случайного процесса требуется описание совместных плотностей для 2, 3, ..., n, ... случайных величин.

В общем случае значение случайного процесса X(t) в n моментов времени t1,t2, …, tn представляет собой n – мерную случайную величину с функцией распределения

Зная совместную функцию распределения случайных величин в моменты t1, t2, …, tn , можно продифференцировать ее и построить функцию плотности распределения.

Математическим ожиданием случайного процесс X(t) называется функция m(t),

зависящая от времени

M (X (t)) m(t ) x pX ( x, t )dx

 Автоковариацией случайного процесс X(t) называется функция RXX(t1,t2), зависящая от двух моментов времени

70. Процесс случайного блуждания и вычисление его характеристик.

Процесс X(t) определен для моментов t, принимающих значения 0, 1, 2, … (дискретный случайный процесс). Случайная величина X(t0) равновероятно принимает значения X(t0-1) +1 или X(t0-1) -1 (шаг вправо или шаг влево), начальное состояние X(0) = 0. Это процесс случайного блуждания по целым точкам числовой оси, начиная из точки 0.

Математическое ожидание суммы случайных величин равно сумме математ ожиданий

дисперсия суммы независимых случайных величин равна сумме дисперсий случайных величин

По определению автоковариация

Если t1 ≤t2 , то положим n = t2 - t1 , тогда для получения величины X(t2) к величине X(t1) нужно добавить n шагов блужданий.

Так как математическое ожидание произведения независимых случайных величин равно

произведению математических ожиданий этих величин, а математическое ожидание X(t1) равно нулю, то

Пусть t1 – фиксированная величина, t1 = 20, а t2 -переменная и t1 ≤t2 , тогда RXX(t1,t2)=20. Если t1 = 20, а t2 принимает любое допустимое значение, то RXX(t1,t2)=min{t1,t2 }, ее график по переменной t2 :

71.Гауссовский случайный процесс.

Случайный процесс X(t) называется гауссовским (нормальным) , если совместная функция

плотности распределения случайных величин X(t1), X(t2), …, X(tn), в моменты t1< t2 < …< tn равна

Где :

- алгебраическое дополнение элемента в определителе D.

Мы ограничиваемся рассмотрением только случая n = 2, то есть рассматриваем совместные функции плотности распределения только двух случайных величин.

72. Стационарный случайный процесс в узком и широком смыслах. Реализации случайного процесса.

Случайный процесс X(t) называется стационарным, если для любых n моментов времени

t1,t2, …, tn и любого приращения времени h совокупные функции

распределения совпадают.

В стационарном процессе при сдвиге по времени совпадают все характеристики входящих в него случайных величин. (Это определение стационарности в узком смысле.)

Для решения некоторых задач бывает достаточно условий:

3)постоянства дисперсии D(t) (то есть D(t) = D) ,

4) условия зависимости функции автоковариации только от разности моментов времени,

R(t1, t2) = R(τ), где τ = t2 - t1.

Такие процессы называются стационарными в широком смысле.

Реализация является результатом отдельного эксперимента, записанная конкретная реализация является детерминированной функцией. Сам случайный процесс в целом должен анализироваться с позиции бесконечной совокупности таких реализаций, что невозможно выполнить для большинства практических задач.

Полной статистической характеристикой процесса является совокупность оценок всех n- мерных плотностей вероятностей. Однако, как экспериментальное оценивание n-мерных плотностей вероятностей процессов, так и их использование при анализе процесса представляет значительные математические трудности.

Поэтому на практике обычно ограничиваются оцениванием одно- и двумерной плотности вероятностей составляющих процесс случайных величин.

Таким образом, для практического решения задач достаточно понятия широкой стационарности процесса.

Реально мы наблюдаем случайный процесс X(t) на ансамбле с конечным числом реализаций

{X1(t), X2(t), …,Xk(t)}. В произвольный момент времени t1 зафиксируем значения всех реализаций {X1(t1), X2(t1), …,Xk(t1)}. Совокупность этих значений представляет собой случайную величину X(t1) и является выборкой (одномерным сечением) случайного процесса X(t) в момент t1.

73.Случайный телеграфный сигнал. Двумерная функция Хевисайда.

Случайный процесс Телеграфный сигнал.

Этот случайный процесс принимает два значения, +1 и -1.

Будем считать, что процесс в любой момент времени равновероятно принимает значения +1 или -1. Это предположение позволит построить распределение случайных величин,

образующих процесс.

Если в момент t1 сигнал принял значение B (равное +1 или -1), то он сохраняет это значение в течение интервала длины τ, после чего переключается на противоположное значение -B , τ – случайная величина, для малых τ вероятность сигнал переключится на другое значение пропорциональна величине τ. Это предположение позволит построить нам совместное распределение случайных величин, образующих процесс.

Удобно ввести обозначение вероятности переключения на другое состояние:

p(одного переключения на интервале длины τ) = ατ, где α – некоторая положительная постоянная. Здесь τ – малая величина.

Пусть x1 =1 (это событие происходит в момент t, вероятность этого события 1/2) , для того, чтобы получить x2 = 1 (в момент t+τ), требуется, чтобы на интервале [t, t+τ] произошло четное число переключений (перемен знака) между +1 и -1. Тогда по аналогии:

автоковариация телеграфного сигнала

+ +

RXX (t,t + ) = (x1 m1 )(x2 m2 )pX1X2 (x1,x2;t,t + )dx1dx2

- -

Записывая функцию плотности, учитывая, что математические ожидания m1 = m2 =0 и группируя:

Вычислим эти интегралы.

По свойству фильтрации для функции Дирака (t) верно равенство

f (t ) (t 1)dt f (1)

 (t) - функция четная, отсюда следует

 Заменяя переменную t на x1 и используя функцию f(x1) = x1 :

x1 ( x1 1)dx1 1

Тогда, выражая двукратные интегралы через однократные

Аналогично второй интеграл (без сомножителя)

Отсюда

Осталось найти вероятности четных и нечетных переключений. Для этого вычислим в предположениях, что

1) p(одно переключение на малом интервале величины τ) имеет порядок малости ατ (было в постановке задачи),

2) два и более переключений не происходят одновременно (не было в постановке! – но предположение разумное).

При таких предположениях - пуассоновское распределение, выведем формулу его вероятности.

Таким образом переходим к следующему вопросу.

После возвращения оттуда ….

Продолжаем вычисление функции автоковариации, осталось найти разность вероятностей четного и нечетного числа переключений на интервале τ. Изменяя порядок суммирования, получаем

Возвращаясь к автоковариации

Вывод функции автоковариации закончен.

Для телеграфного сигнала выполнены все четыре условия стационарности в широком смысле,

то есть, телеграфный сигнал - стационарный процесс в широком смысле. (Более того,

этот процесс стационарный и в узком смысле – не доказываем).

двумерная функция Хевисайда : была где-то в середине вывода этой мудистики (тут нету)

Простой проверкой значений эту функцию можно выразить через обычные одномерные функции Хевисайда :

1(x1,x2 ) = 1(x1) 1(x2 )

Другая схема вывода автоковариации (без δ-функции). Можно было найти функцию автоковариации вычисляя ковариацию дискретных случайных величин без явного построения функции совместной плотности

Мат ожидание телеграфного сигнала m = 0, вероятность произведения

задается распределением

Получаем

74.Вывод вероятности пуассоновского распределения.

... в предположениях, что

1) p(одно переключение на малом интервале величины τ) имеет порядок малости ατ (было в постановке задачи),

2) два и более переключений не происходят одновременно (не было в постановке! – но предположение разумное).

При таких предположениях - пуассоновское распределение, выведем формулу его вероятности.

Выведем формулу вначале для интервала τ =1. Разделим интервал на N равных малых интервалов Δτ = 1/N, таких, чтобы на каждом малом интервале Δτ происходило либо одно событие (переключение), либо ни одного. Тогда вероятность p1 того, что на малом интервале произошло одно событие, равна αΔτ, ни одного события 1- α Δτ.

Вероятность того, что на n малых интервалах произошли события, равна (αΔτ)n, на остальных N - n интервалах событие не произошло, равна (1- αΔτ)N-n. Получена схема Бернулли для N испытаний, в этой схеме вероятность n удач, N – n неудач (из N испытаний) равна

Предел этого выражения и будет искомой вероятностью переключений:

Раскроем выражение под знаком предела

Избавимся от одной переменной, заменив

и упростим выражение для факториалов

Выражение

Окончательно

Для временнОго интервала τ в доказательстве отношение заменяется на и тогда

75. Эргодический случайный процесс. Критерий Слуцкого.

Эргодическим называется стационарный в узком смысле случайный процесс, для которого по его одной реализации можно статистически достоверно оценить все его параметры. При этом реализация должна быть достаточно длинной, чтобы оценки были достоверными.

Для практической проверки эргодичности стационарного процесса можно применить

условие Слуцкого:

76.Свойства функции автоковариации.

Оценку степени зависимости случайных величин X(t1) и X(t2) (мгновенные значений процесса X(t) ) в произвольные моменты времени t1 и t2 выполняет функция автоковариации

RXX (t1,t2 ).

1. Функция автоковариации не изменяется при перестановке аргументов: RXX(t1, t2) = RXX(t2, t1) . Эти следует из равенства