Оценка погрешностей результатов прямых равноточных измерений

Прямыми называются измерения, в результате которых находят непосредственно искомые значения величин. В этом случае измеряемую величину находят прямым сравнением с её мерой или по показаниям прибора. Результаты, получаемые при прямых измерениях постоянной физической величины, называются равноточными или равнорассеянными [8].

Равнорассеянные  это одинаково доверяемые измерения при условии проведения их с одинаковой тщательностью при повторных наблюдениях, в одних и тех же условиях, с помощью одинаковых средств измерений, одними и теми же лицами и одинаковом числе наблюдений [4].

Количество измерений может быть различным, однако если случайные составляющие малы по сравнению с систематическими составляющими погрешностей и соответственно ими пренебрегать нельзя, для определения характеристик погрешностей измерений, наряду с определением систематических составляющих погрешностей, необходимо проводить многократные измерения измеряемой физической величины для определения случайных составляющих.

При многократных измерениях отдельное измерение принято называть наблюдением, и, соответственно, результат отдельного измерения при проведении многократных измерений называется результатом наблюдения.

Однако при многократных измерениях не имеется возможности проведения бесконечно большого количества наблюдений, следовательно, не имеется возможности принятия в качестве результата измерения истинного значения измеряемой величины и в качестве характеристик случайных величин принимаются не истинные, а приближенные оценки этих характеристик. Значения измеренной величины и оценок ее характеристик, в отличие от самих характеристик, являются случайными величинами, зависящими от количества проведенных наблюдений.

Многократные измерения проводятся, как правило, для уменьшения влияния случайных погрешностей. Результат каждого измерения при этом дает оценку измеряемой величины [2].

При статистической обработке группы результатов прямых многократных независимых измерений выполняют определённые последовательные операции.

1.1 Алгоритм статистической обработки результатов измерений

Алгоритм статистической обработки результатов измерений включает в себя несколько этапов.

На первом этапе исключают систематические погрешности. Если известно, что все результаты наблюдений имеют одинаковую систематическую погрешность, ее исключают из результата измерений.

На втором этапе вычисляют оценку измеряемой величины. Измеряемой величиной является среднее арифметическое результатов измерений .

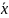Далее вычисляют среднее квадратическое отклонения (СКО). Для нахождения СКО используется такая формула:

(1.1)

,

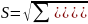где n число измерений;

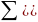сумма квадратов абсолютных отклонений;

отсюда:

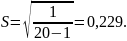
Затем вычисляют СКО среднего арифметического для окончательной записи результата измерения. Его определяют по формуле:

(1.2)

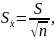
отсюда:

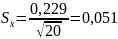
На пятом этапе обработки проверяют наличие грубых погрешностей. Если в ряде измерений обнаружены грубые погрешности, то их исключают. Для исключения промахов – грубых погрешностей, используют критерий Граббса, он основан на предположениях о том, что группа результатов измерений принадлежит нормальному распределению.

Затем необходимо проверить гипотезу о принадлежности результатов измерений нормальному распределению.

После проводят вычисление доверительных границ погрешности среднего арифметического согласно формуле:

(1.3)

,

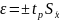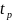
где  коэффициент Стьюдента, который в зависимости от доверительной вероятности и числа результатов измерений определяется по таблице;

p  принятая при обработке результатов измерений доверительная вероятность.

следовательно:

.

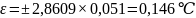После округления погрешности результата получим: t = (83,16 ± 0,146) ⁰С при p = 0, 99.

На восьмом этапе оценивают доверительные границы случайной погрешности. Согласно рекомендациям Р. 50.2.038-2004 [7], доверительные границы случайной погрешности результата однократного измерения можно оценить по формуле:

(1.4)

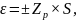
где Z_p  квантиль функции нормированного распределения для вероятности

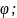
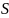
 определённое экспериментально СКО результатов измерений, которое характеризует рассматриваемый метод.

Далее определяют вероятность распределения 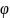по формуле:

(1.5)

,

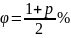следовательно:

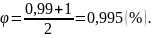
Из задания известно, что тогда согласно формуле (1.4) доверительные границы случайной погрешности результата однократного измерения составят:

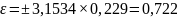
После чего необходимо представить эту погрешность в относительной форме. Для этого используют следующую формулу:

(1.6)

где  среднее арифметическое значение температуры, полученное при обработке эксперементальных данных. Используется в качестве действительного значения измеряемой велечины.

Из условия задания известно, что = 83,16, следовательно погрешности результата однократного измерения в относительной форме согласно формуле (1.6) составит:

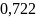Так как = 0,9 %, что превышает 0,5%, следовательно, метод не пригоден для получения однократного результата измерений с требуемой точностью. Погрешность при однократных измерениях в абсолютной форме с доверительной вероятностью р = 0,99, составит ± ⁰С.

В соответствии с ГОСТ Р. 8. 736-2011, используя, значение S полученное при изучении метода измерения погрешность вычисляют по формуле:

(1.7)

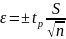
откуда:

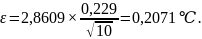
Для расчёта используем значение коэффициента Стьюдента при p = 0,99 и n1 = 9

На следующем этапе определяют необходимое количество опытов. Для чего пользуются формулой:

(1.8)

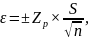
откуда:

(1.9)

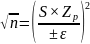
Выразим допускаемую погрешность ± 0,1 % в абсолютной форме, используя следующую формулу:

(1.10)

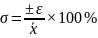
откуда:

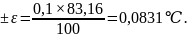
Тогда согласно формуле (1.9) определим количество опытов:

то есть необходимо провести семьдесят пять измерений.

На последнем этапе, для оценки влияния замены коэффициента Стьюдента на Квантиль нормального распределения, определяют доверительные границы погрешности среднего арифметического полученного при выборке 75 опытов при t_р = 2,6267. Согласно формуле (1.7) получим:

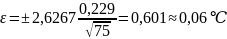
Выразим эту погрешность в относительной форме, согласно формуле (1.10) она составит:

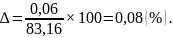
Исходя из этого, можно говорить о том, что при большом числе опытов замена коэффициента Стьюдента на квантиль нормального распределения привела к уменьшению погрешности.