2 Метод проектирования устройств фильтрации по рабочим параметрам

Под электрическим фильтром понимается устройство, пропускающее электрические колебания одних частот и задерживающее колебания других частот.

Одним из способов проектирования фильтров является каскадный способ. Его преимуществом является простота реализации, возможность индивидуальной настройки отдельных звеньев и хорошее согласование по входу и выходу за счет применения ОУ. Проектирования фильтра на основе способа каскадной реализации независимо от типа фильтра содержит ряд этапов:

1. Расчет структурной схемы устройства.

2. Выбор аппроксимации.

3. Определение порядка фильтра.

4. Выбор структуры фильтра.

5. Схемная реализация.

6. Расчет и выбор элементов схемы.

7. Связь фильтра с источником сигнала (ИС) и нагрузкой.

8. Схемотехническое моделирование устройства и его оптимизация.

По результатам моделирования может быть принято решение о возврате на один из ранних этапов проектирования, т.е. данная процедура носит итерационный характер.

На рисунке 2.1 показан фильтр, коэффициент передачи которого определяется следующим образом:

В выражении для K(p) заменяем и преобразовываем: . Получаем зависимости для частотных и временных характеристик фильтра:

• выражение под знаком модуля 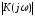– амплитудно-частотная характеристика (АЧХ);

• выражение – фазо-частотная характеристика (ФЧХ);

• переходная характеристика (ПХ);

• импульсная характеристика (ИХ);

• характеристика рабочего затухания (ХРЗ);

• характеристика группового времени задержки (ХГВЗ).

Коэффициент передачи фильтра выразим с помощью полиномов:

,

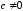
Порядком фильтра n называют наибольшую степень р в знаменателе. G(p)-полином степени m, корни которого могут лежать, где угодно на комплексной плоскости. V(p)-полином Гурвица, степени n с вещественными коэффициентами, корни которого могут лежать только в левой полуплоскости мнимой оси.

,

где , , .

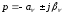Полюсы должны иметь отрицательные действительные части и степень полинома в числителе должна быть равна или меньше степени полинома в знаменателе. Эти условия являются необходимыми для физически реализуемого фильтра.

При проектировании фильтров всегда имеют ввиду тот факт, что идеальные АЧХ физически не реализуемы. Можно лишь стремиться к наилучшему приближению (или аппроксимации), совместимому с требованиями, предъявляемыми к фильтру.

Задача аппроксимации состоит в том, чтобы синтезировать некоторую функцию частоты, удовлетворяющую требованиям к АЧХ или ХРЗ разрабатываемого фильтра.

Фильтрующие свойства часто оцениваются величиной относительного затухания, определяемой в децибелах как

.

Примерный вид реальных характеристик затухания для ФНЧ приведен на рисунке 2.3.

Область частот пропускаемых колебаний, для которых АЧХ изменяется незначительно, называется полосой пропускания и находится в диапазоне частот от 0 до ω_p. Область частот задерживаемых колебаний (ω_a до ∞), для которых АЧХ не превосходит некоторого малого заданного значения, называется полосой задерживания.

Условная граница между этими полосами называется частотой среза ω_c и находится в пределах переходной полосы. A_p – максимальное затухание в полосе пропускания; A_a – минимальное затухание в полосе задерживания.

Аппроксимация АЧХ практически сводится к выбору таких коэффициентов полиномов, которые обеспечивают не только аппроксимацию АЧХ, но и физическую реализуемость фильтра.

Известно довольно много аппроксимаций, отвечающих вышеуказанному условию, однако наибольшее распространение получили три из них: Баттерворта, Чебышева и Золотарёва-Кауэра. Каждый из этих типов имеет свои особенности, которые хорошо видны на графике зависимости рабочего затухания от частоты рис.2.4

Все они предназначены для ФНЧ, но довольно просто могут быть преобразованы в аппроксимации других типов фильтров.

Следует отметить следующее. В теории фильтрации принято так называемое нормирование по частоте, приводящее расчет фильтров (ФНЧ, ФВЧ, ПФ, ЗФ), работающих на различных частотах, к расчету некоторого нормированного фильтра с определенной частотой среза. В качестве такого нормированного фильтра, называемого прототипом, принимается ФНЧ.

Наиболее простой является аппроксимация Баттерворта. Данная аппроксимация дает максимально плоскую АЧХ в полосе пропускания при заданном n. АЧХ имеет максимум при ω = 0 и монотонно убывает с ростом частоты. Данную аппроксимацию следует применять, если накладывается требование монотонности АЧХ во всем диапазоне частот.

В аппроксимации Чебышева в отличие от предыдущего, допускается некоторая немонотонность АЧХ типа пульсаций в полосе пропускания, т.е. затухание колеблется между нулем и заданным максимальным уровнем. В полосе задерживания пульсации отсутствуют. Иногда данную аппроксимацию называют равноволновой. Число пульсаций увеличивается с ростом порядка фильтра. За счет появления пульсаций крутизна спада АЧХ возрастает по сравнению с фильтром Баттерворта того же порядка.

Аппроксимация Кауэра является логическим развитием идеи равноволнового фильтра и допускает пульсации как в полосе пропускания, так и в полосе задерживания. За счет этого реализуется еще большая крутизна спада АЧХ, чем у фильтра Чебышева.

В данной курсовой работе проектируется фильтр нижних частот, со структурой на операционных усилителях Саллена-Кея. Пятый порядок фильтра, аппроксимация частотных характеристик Чебышева. Неравномерность в полосе пропускания .

По условию заданны данные:

В задании по курсовому проекту даны коэффициенты С, α_i, β_i, в нормированном виде, то необходимо осуществить денормирование. Коэффициент передачи ФНЧ в нормированном виде можно записать следующим образом:

(2.1)

Если в этой формуле сделать замену переменной , где , то мы получим выражение для коэффициента передачи в денормированном виде:

(2.2)

Приведем формулу к более удобному виду:

(2.3)

Где ,

,

,

,

После подсчетов получаем:

,

,

,

,

,

,

,
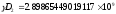